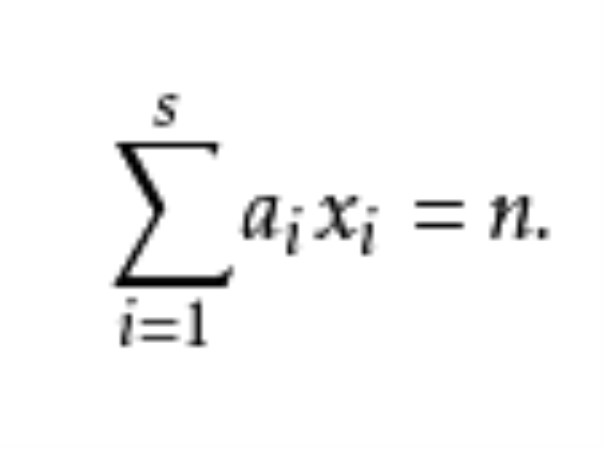一次不定方程

一次不定方程(linear indeterminate equation)亦稱線性不定方程，是一類重要的不定方程，指未知數多於一個的一次方程。設a₁, a₂,...,a_n是非零整數，b是整數，稱關於未知數x₁, x₂,...,x_n(n≥2)的方程a₁x₁+a₂x₂+...+a_nx_n= b是n元一次不定方程。方程a₁x₁+a₂x₂+...+a_nx_n= b有整數解的充要條件是(a₁, a₂,...,a_n)|b。

基本介紹

• 中文名：一次不定方程
• 外文名：linear indeterminate equation
• 別稱：線性不定方程
• 所屬學科：數學
• 所屬問題：初等數論(不定方程)

一次不定方程簡介

設a₁, a₂,...,a_n是非零整數，b是整數，稱關於未知數x₁, x₂,...,x_n(n≥2)的方程

是n元一次不定方程，或稱非零的a_i∈Z(i=1，2，…，s)，s>1，且n∈Z的方程

是s元一次不定方程。

若存在整數滿足方程，則稱是方程的解，或說是方程的解。

定理1 方程a₁x₁+a₂x₂+...+a_nx_n= b有整數解的充要條件是(a₁, a₂,...,a_n)|b。

設a_i>0(i=1，2，…，s)，(a₁，a₂，…，a_s)=1，考慮方程(1')的非負整數解x_i≥0(i=1，2，…，s)，存在僅與a₁，a₂，…，a_s有關的數F_a1，…，a_s，當n>F_a1，…，a_s時，方程(1')有非負整數解。令A(n)為其解數，則

求出F_a1，a₂，…，a_s的最佳值 ɡ_a1，a₂，…，a_s就是弗羅貝尼烏斯問題。

二元一次不定方程及其求解

設a,b,c是整數，形如ax+by=c的方程是二元一次不定方程。

定理2 設a,b,c是整數，方程ax+by=c若有解(x₀,y₀)，則它的一切解具有的形式，其中。

定理1和定理2說明了解二元一次不定方程的歩驟：

(1)判斷方程是否有解，即(a，b)|c是否成立；

(2)利用輾轉相除法求出x₀,y₀，使得ax₀+by₀=(a,b)；

(3)寫出方程ax+by=c的解，其中。

多元一次不定方程及其求解

定理3 設a₁, a₂,...,a_n,b是整數，再設(a₁, a₂,...,a_n-1) = d_n-1，(a₁, a₂,...,a_n)=d_n，則是方程(1)的解的充分必要條件是存在整數t,使得是方程組

的解。

定理3說明了求解n元一次不定方程的方法：先解方程組中的第二個方程，再解方程組中的第一個方程，於是，解n元一次不定方程就化為解n-1元一次不定方程，重複這個過)程，最終歸結為求解二元一次不定方程。

記(a₁, a₂) = d₂，(d₂,a₃) = d₃,...,(d_n-2,a_n-1) =d_n-1，(d_n-1,a_n) = d_n。

逐個地解方程

並且消去中間變數就可以得到方程的解。