定義,作用,頻數分布直方圖,定義,特點,目的,繪製注意事項,製作方法,套用步驟,實例,區域直方圖,用法,注意事項,繪製方法,分析質量,形狀分析,概述,孤島型,雙峰型,折齒型,陡壁型,偏態型,平頂型,比較分析,理想型,偏向型,無富餘型,能力富餘型,能力不足型,直方圖均衡化,直方圖拉伸,直方圖匹配,
定義 在質量管理中,如何預測並監控產品質量狀況?如何對質量波動進行分析?直方圖就是一目了然地把這些問題圖表化處理的工具。它通過對收集到的貌似無序的數據進行處理,來反映產品質量的分布情況,判斷和預測產品質量及不合格率。
直方 圖又稱
質量分布圖, 它是表示資料變化情況的一種主要工具。用直方圖可以解析出資料的規則性,比較直觀地看出產品質量特性的分布狀態,對於資料分布狀況一目了然,便於判斷其總體質量分布情況。
在製作直方圖時,牽涉統計學的概念,首先要對資料進行分組,因此如何合理分組是其中的關鍵問題。按組距相等的原則進行的兩個關鍵數位是分組數和組距。是一種幾何形圖表,它是根據從生產過程中收集來的
質量數據 分布情況,畫成以組距為底邊、以頻數為高度的一系列連線起來的直方型矩形圖,如圖所示。
作直方圖的目的就是通過觀察圖的形狀,判斷生產過程是否穩定,預測生產過程的質量。具體來說,作直方圖的目的有:
1判斷一批已加工完畢的產品;蒐集有關數據。
直方圖將數據根據差異進行分類,特點是明察秋毫地掌握差異。
1)估算可能出現的不合格率;
2)考察工序能力估算法
3)判斷質量分布狀態;
4)判斷施工能力;
3統計一組數據的常見值。
作用 直方圖的常見作用有以下三點:
直方圖與標準的對照 (1)顯示質量波動的狀態;
(2)較直觀地傳遞有關過程質量狀況的信息;
(3)通過研究質量波動狀況之後,就能掌握過程的狀況,從而確定在什麼地方集中力量進行質量改進工作。
頻數分布直方圖
定義 在統計數據時,按照頻數分布表,在平面直角坐標系中,橫軸標出每個組的端點,縱軸表示頻數,每個矩形的高代表對應的頻數,稱這樣的統計圖為頻數分布直方圖。
特點 ①能夠顯示各組頻數分布的情況;
目的 作直方圖的目的就是通過觀察圖的形狀,判斷生產過程是否穩定,預測生產過程的質量。
繪製注意事項 a. 抽取的樣本數量過小,將會產生較大誤差,可信度低,也就失去了統計的意義。因此,樣本數不應少於50個。
製作方法 ①集中和記錄數據,求出其最大值和最小值。數據的數量應在100個以上,在數量不多的情況下,至少也應在50個以上。 我們把分成組的個數稱為組數,每一個組的兩個端點的差稱為組距。
③計算組距的寬度。用最大值和最小值之差去除組數,求出組距的寬度。
套用步驟 (1)收集數據。作直方圖的數據一般應大於50個。
實例 現以某廠生產的產品重量為例,對套用直方圖的步驟加以說明:
(1)收集數據。作直方圖的數據一般應大於50個。本例 在生產過程中收集了100個數據,列於表一中。
(2)確定數據的
極差 (R)。用數據的最大值減去最小值 求得。本例最大值X max =48(cg),最小值X min =1(cg),所以極差 R= 48-1= 47(cg).
直方圖套用案例圖 (3)確定
組距 (h)。先確定直方圖的
組數 ,然後以此組數去除極差,可得直方圖每組的寬度,即組距。組數的確定要適當。組數太少,會引起較大計算誤差;組數太多,會影響數據分組規律的明顯性,且計算工作量加大。組數(k)的確定可參考組數(k)選用表二。
(4 )確定各組的界限值。為避免出現數據值與組界限值重合而造成頻數據計算困難,組的界限值單位應取最小測量單位的1/2。本例最小測量單位是個位,其界限值應取0.5。分組時應把數據表中最大值和最小值包括在內。
第一組下限值為:最小值-0.5=0.5;
第一組上限值為:第一組下限值加組距,即0.5+5=5.5;
第二組下限值就是第一組的上限值,即5.5;
第二組上限值就是第二組的下限值加組距,即5.5+5=10.5;
第三組以後,依此類推定出各組的組界。
(5)編制頻數分布表。把多個組上下界限值分別填入頻數分布表內,並把數據表中的各個數據列入相應的組,統計各組頻數據(f )。
(7)按頻數值比例畫
縱坐標 。以觀測值數目或百分數表示。
(8)畫直方圖。按縱坐標畫出每個長方形的高度,它代表取落在此長方形中的數據數。(注意:每個長方形的寬度都是相等的。)在直方圖上應標註出
公差 範圍(T)、
樣本容量 (n)、樣本平均值(X)、樣本標準偏差值(s)和-x的位置等。
區域直方圖
用法 您可以通過區域直方圖對一個數據集中的值在另一個數據集類中的頻數分布進行研究。例如,
土地利用 類中的坡度分布、高程類中的降雨分布或警務區附近的犯罪分布。
區域定義為輸入中具有相同值的所有區。各區無需相連。柵格和要素數據集都可用於區域輸入。如果區域輸入和值輸入均為具有相同解析度的柵格,則可直接使用它們。如果解析度不同,則可先套用內部重採樣以使其相一致,然後再執行區域操作。
倘若輸入中存在任何 NoData 像元,重採樣就可能在輸出中產生比您預期更大的 NoData 區域。要避免此種情況,或者重新採樣粗糙輸入
柵格 ,提高輸入柵格的解析度,或者在“柵格分析”環境下將像元大小設定為輸入的最小值。
如果區域輸入為柵格數據集,則該輸入必須具有屬性表。通常會自動為整型柵格數據創建屬性表,但是某些情況下可能不會這樣做。您可以使用構建柵格屬性表來創建一個屬性表。建議您僅使用柵格作為區域輸入,因為這可使您更好地控制“矢量至柵格”轉換。這將有助於確保您始終獲得預期的結果。
如果區域輸入是要素數據集,則可在內部對其套用“矢量至柵格”轉換。要確保轉換結果與值柵格完全對齊,建議您檢查環境設定和柵格設定中的範圍和捕捉柵格是否設定正確。
由於內部柵格必須具有屬性表,因此在轉換中不創建屬性表的情況下將會發生錯誤。如果發生此錯誤,則使用要素轉柵格、面轉柵格、點轉柵格或折線轉柵格直接轉換要素
數據集 。按先前提示中所述內容為其生成屬性表,然後使用生成的柵格作為“區域”輸入。
如果區域輸入為要素相對較小的要素數據集,則需要牢記,信息的解析度需要適合於值柵格的解析度。如果單個要素的區域相似於或小於值柵格中單個像元的區域,則在要素轉柵格轉換過程中,某些區域可能不會顯示。要對此進行顯示,需嘗試使用適當的要素轉柵格轉換工具將要素數據集轉換為柵格,然後將解析度指定為值柵格的解析度。通過此轉換產生的結果會指明區域操作的默認輸出將是什麼。
如果輸出中的結果比您可能已預期的少,則需要確定表示要素輸入細節的適當的柵格解析度,然後使用此解析度作為“柵格分析環境設定”的像元大小。
如果區域輸入為點要素數據集,則其可能具有值輸入柵格的任何特定像元內所含的多個點。對於這種像元,區域值將通過具有最高要素 ID 的點來確定。
如果區域要素輸入具有疊置的面,則無法為每一個單獨的面執行區域分析。因為要素輸入已轉換為柵格,所以每個位置只能擁有一個值。
另一種方法就是要為每個面區域反覆進行分區統計並核對結果。
區域欄位必須為整型或字元串類型。
在指定輸入區域數據時,默認區域欄位將為第一個可用的有效欄位。如果無其他有效欄位存在,則 ObjectID 欄位(如OID 或 FID)將為默認欄位。
輸入值柵格上的像元屬於像元中心所在的區域。在此情況下,這些區域是在向柵格和重新採樣進行了任何必要轉換後的區域。
在直方圖中,每個區域的類(條柱)的數量由輸入賦值柵格確定。
如果指定圖層,則圖層的符號系統定義類的數量。
如果指定數據集,則在默認情況下將有 256 個類,除非輸入是具有少於 26 個唯一值的整型(在此情況下,它將是唯一值的總數)。
默認情況下不生成區域直方圖。要在工具運行時創建區域直方圖,可指定輸出圖形名稱。
該圖形只是臨時圖形(在記憶體中)。要創建該圖形的永久版本,可使用保存圖表工具創建 .grf 圖形檔案,或者以該工具中提供的一種其他格式進行創建。
注意事項 a. 抽取的樣本數量過小,將會產生較大誤差,可信度低,也就失去了統計的意義。因此,樣本數不應少於50個。
b. 組數 k 選用不當,k 偏大或偏小,都會造成對分布狀態的判斷有誤。
c. 直方圖一般適用於計量值數據,但在某些情況下也適用於計數值數據,這要看繪製直方圖的目的而定。
d. 圖形不完整,標註不齊全,直方圖上應標註:公差範圍線、平均值 的位置(點畫線表示)不能與公差中心M相混淆;圖的右上角標出:N、S、C p或 CPK.
繪製方法 ①集中和記錄
數據 ,求出其最大值和最小值。數據的數量應在100個以上,在數量不多的情況下,至少也應在50個以上。 我們把分成組的個數稱為
組數 ,每一個組的兩個
端點 的差稱為
組距 。
②將數據分成若干組,並做好記號。分組的數量在5-12之間較為適宜。
③計算組距的寬度。用最大值和最小值之差去除
組數 ,求出
組距 的寬度。
④計算各組的界限位。各組的界限位可以從第一組開始依次計算,第一組的下界為最小值減去最小測定單位的一半,第一組的
上界 為其下界值加上組距。第二組的下界限位為第一組的上界限值,第二組的下界限值加上組距,就是第二組的上界限位,依此類推。
⑥作直方圖。以組距為底長,以頻數為高,作各組的
矩形圖 。
分析質量 作直方圖是的目的是為了研究產品質量的分布狀況,據此判斷生產過程是否處在正常狀態。直方圖為QC七大工具之一。因此在畫出直方圖後要進一步對它進行觀察和分析。在正常生產條件下,如果所得到的直方圖不是標準形狀,或者雖是標準形狀,但其分布範圍不合理,就要分析其原因,採取相應措施。
(1)通過直方圖判斷生產過程是否有異常。對直方圖有些參差不齊不必太注意,主要應著眼於圖形的整個形狀。常見的直方圖分布圖形大體上有六種,如圖所示。
①理想的圖形;
②多是因為測量和讀數有問題或是數據分組不當所引起的;
③多是因加工習慣造成的;
④多是加工條件的變動造成的;
⑤多是兩種不同生產條件的數據混在一起造成的;
⑥多是由於生產過程中某種緩慢的傾向起作用所至。
(2)運用直方圖勘量生產的質量狀況。將直方圖與公差範圍相比較,看直方圖是否都落在公差要求的範圍之內,可以提高生產的質量狀況。這種對比大體上存在六種情況,如下圖所示。
①理想的情況;
②經濟性不好,需降低加工精度;
③需要採取措施適當縮小分布;
④過分偏離公差中心,可能造成廢品;
⑤完全不留餘地,容易出現廢品,應採取措施調整
⑥已經產生廢品,應停產檢查。
形狀分析
概述 正常型是指過程處於穩定的圖型,它的形狀是中間高、兩邊低,左右近似對稱。近似是指直方圖多少有點參差不齊,主要看整體形狀。如下
圖例 :
異常型直方圖種類則比較多,所以如果是異常型,還要進一步判斷它屬於哪類異常型,以便分析原因、加以處理。下面介紹幾種比較常見的:
孤島型 在直方圖旁邊有孤立的小島出現,當這種情況出現時過程中有異常原因。如:原料發生變化,不熟練的新工人替人加班,測量有誤等,都會造成孤島型分布,應及時查明原因、採取措施。
孤島型直方圖
雙峰型 當直方圖中出現了兩個峰,這是由於觀測值來自兩個總體、兩個分
布的數據混合在一起造成的。如:兩種有一定差別的原料所生產的產品混合在一起,或者就是兩種產品混在一起,此時應當加以分層。
雙峰型直方圖
折齒型 當直方圖出現凹凸不平的形狀,這是由於作圖時數據分組太多,測量儀器誤差過大或觀測數據不準確等造成的,此時應重新收集數據和整理數據。
折齒型直方圖
陡壁型 當直方圖像高山的陡壁向一邊傾斜時,通常表現在產品質量較差時,為了符合標準的產品,需要進行全數檢查,以剔除不合格品。當用剔除了不合格品的產品數據作頻數直方圖時容易產生這種陡壁型,這是一種非
自然形態 。
陡壁型直方圖
偏態型 偏態型直方圖是指圖的頂峰有時偏向左側、有時偏向右側。
偏態型直方圖 由於某種原因使下限受到限制時,容易發生偏左型。如:用標準值控制下限,擺差等形位公差,不純成分接近於0,疵點數接近於0或由於工作習慣都會造成偏左型。
由於某種原因使上限受到限制時,容易發生偏右型。如:用標準尺控制上限,精度接近100%,合格率也接近100%或由於工作習慣都會造成偏右型。
平頂型 當直方圖沒有突出的頂峰,呈平頂型,然而形成這種情況一般有三種原因。 A、與雙峰型類似,由於多個總體、多總分布混在一起。 B、由於生產過程中某中緩慢的傾向在起作用,如工具的磨損、操作者的疲勞等。 C、質量指標在某個區間中均勻變化。
平頂型直方圖
比較分析 當直方圖的形狀呈正常型時,即工序在此時刻處於穩定狀態時,還需要進一步講直方圖同規格界限(即公差)進行比較,以分析判斷工序滿足公差要求的程度。
這裡規格的上限用Tu表示,Tl為規格的下限,公差中心M=
,樣本的分布中心為
,樣本的標準差為s。
下面將與規格界限比較的常見幾種典型狀態,及其分析、控制要點結合圖型加以說明。
理想型 圖型對稱分布,樣本分布中心
與公差中心M近似重合,分布在公差範圍內且兩邊有一定餘量,是理想狀態。因此,可保持狀態水平加以監督。
偏向型 樣本分布中心
比公差中心M有較大偏移,這種情況下,稍有不慎就會出現不合格。因此要調整分布中心與公差中心近似重合。
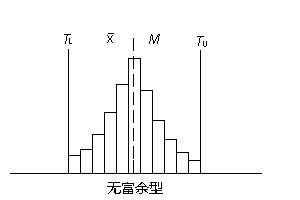
無富餘型 樣本分布中心
與公差中心M近似重合,但兩邊與規格的上、下限緊緊相連,沒有餘地,表明過程能力已到極限,非常容易出現失控,造成不合格。因此,要立即採取措施,提高過程能力,減少標準偏差。
能力富餘型 樣本分布中心
與公差中心M近似一致,但兩邊與規格上、下限有很大距離,說明工序能力出現過剩,經濟性差。因此,可考慮改變工藝,放寬加工精度或減少檢驗頻次,以降低成本。
能力不足型 樣本中心
與公差中心M近似重合,但分布已超出上、下限。這時不合格已經出現。因此,要採取措施提高加工精度,減少標準偏差。
能力不足,左、右超限
樣本中心
與公差中心M有偏移且分布有部分已超出上、下限。這種情況比較複雜。首先,調整分布中心,使之與公差中心近似重合,如果,調整後,不合格消失,說明不合格主要是由於某個系統原因造成的,這時,在深入分析過程能力是否需要繼續提升等。其次,如果經調整,分布中心與公差中心已近似重合,但仍有不合格,則說明過程能力已嚴重不足,樣本分散程度過大,要繼續提高加工精度,減少標準偏差。
攝影中的直方圖橫坐標是表示亮度分布,左邊暗,右邊亮,縱坐標表示像素分布。直方圖能夠顯示一張照片中色調的分布情況,揭示了照片中每一個亮度級別下像素出現的數量,根據這些數值所繪出的圖像形態,可以初步判斷照片的曝光情況,直方圖是照片曝光情況最好的回饋。無論照片是有豐富的
高光 表現還是
曝光 過度了,還是有飽滿的細部暗調,或者是細節根本分辨不清,直方圖都能很直觀的顯示。
當今的大多數數位相機都有內置的直方圖顯示功能,有單獨顯示的有疊加在圖像上顯示的;當拍完一張照片的時候,就可以開始使用直方圖來了解整個圖像的色調範圍。在拍攝期,攝影師就可以用它來了解照片是不是控制在想要的曝光範圍內。
能力不足,左、右超限 從理論上說,一張曝光良好的照片,在不同的亮度級別下細節都應該非常豐富,各亮度值上都有
像素 分布,像一座起伏波盪的小山丘,為了方便觀察,把直方圖劃分為5個區:每個區代表一個亮度範圍,左邊為極暗部、暗部,中間為中間調,右邊是亮部和極亮部,根據這些不同亮度範圍下像素出現的數量,對於
高調照片 (明亮調子且細節豐富的圖片)山丘的峰頂應該集中在直方圖右邊的亮部區,對於
低調照片 (深色調子且細節豐富的圖片)山丘的峰頂應該集中在直方圖左邊的暗部區域,如果山丘覆蓋了整個區域,說明曝光情況正好且細節清晰可見。
遙感影像的直方圖
圖像直方圖描述了圖像中每個亮度值DN的像元數量的統計分布。它通過每個亮度值的
像元 數除以圖像中總得像元數,即
頻率直方圖 。在很多
遙感套用 中,直方圖是遙感圖像中所包含的信息的一種有用的圖示。每個波段的直方圖能提供關於原始圖像質量的信息,如其
對比度 的強弱,是否多峰值等。
直方圖均衡化 直方圖均衡 化,是通過使用累積函式對灰度值進行“調整”以實現對比度的增強。直方圖均衡化處理的“中心思想”是把原始圖像的灰度直方圖從比較集中的某個灰度區間變成在全部灰度範圍內的均勻分布。直方圖均衡化就是對圖像進行非線性拉伸,重新分配圖像像素值,使一定灰度範圍內的像素數量大致相同。
簡單說就是把給定圖像的直方圖分布改變成“均勻”分布直方圖分布。其缺點:①變換後圖像的灰度級減少,某些細節消失;②某些圖像,如直方圖有高峰,經處理後對比度不自然的過分增強。
直方圖拉伸 直方圖拉伸的主要作用就是將灰度間隔小的圖像的灰度間隔擴大,以便於觀察圖像。直方圖拉伸是通過對比度拉伸對直方圖進行調整,從而“擴大”前景和背景灰度的差別,以達到增強對比度的目的。
直方圖匹配 直方圖匹配 又叫直方圖規定化,是指把原圖像的直方圖變換為某種指定形態的直方圖或某一種參考圖像的直方圖,然後按照已知直方圖調整原圖像各個像元的灰度值,最後得到一幅直方圖匹配的圖像。
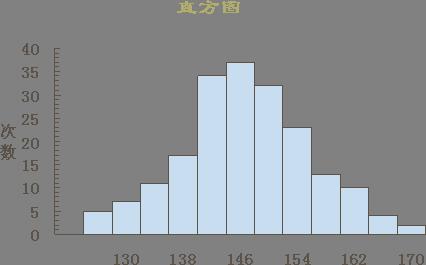
 直方圖與標準的對照
直方圖與標準的對照 直方圖套用案例圖
直方圖套用案例圖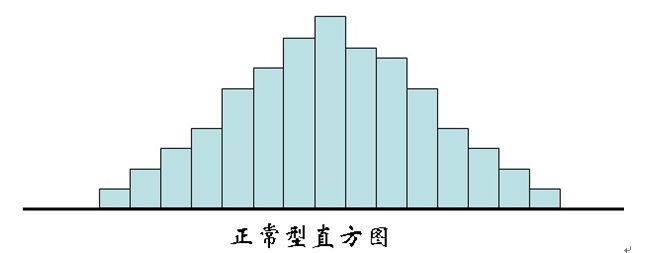
 孤島型直方圖
孤島型直方圖 雙峰型直方圖
雙峰型直方圖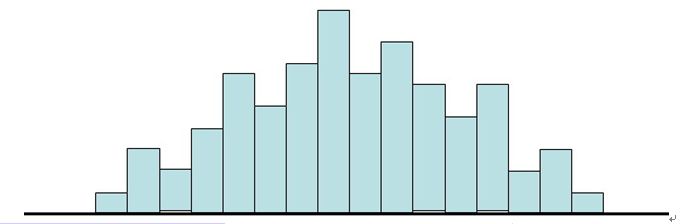 折齒型直方圖
折齒型直方圖 陡壁型直方圖
陡壁型直方圖 偏態型直方圖
偏態型直方圖 平頂型直方圖
平頂型直方圖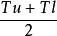






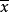



 能力不足,左、右超限
能力不足,左、右超限
