基本介紹
- 中文名:頻率直方圖
- 外文名:frequency histogram
- 亦稱:頻率分布直方圖
- 所屬學科:數學(統計學)
- 相關概念:頻數、頻率等
基本介紹



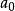

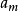
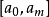
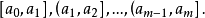
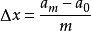


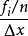

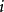
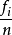




例題解析



區間 | 頻數 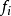 | 頻率  |
[3,4] | 1 | 1/50 |
(4,5] | 6 | 6/50 |
(5,6] | 11 | 11/50 |
(6,7] | 15 | 15/50 |
(7,8] | 9 | 9/50 |
(8,9] | 6 | 6/50 |
(9,10] | 2 | 2/50 |
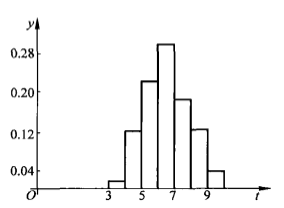 圖1
圖1
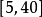




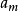
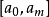
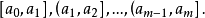
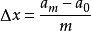


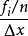

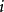
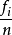
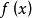



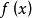

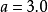



區間 | 頻數 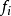 | 頻率  |
[3,4] | 1 | 1/50 |
(4,5] | 6 | 6/50 |
(5,6] | 11 | 11/50 |
(6,7] | 15 | 15/50 |
(7,8] | 9 | 9/50 |
(8,9] | 6 | 6/50 |
(9,10] | 2 | 2/50 |
 圖1
圖1
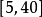
頻率直方圖(frequency histogram)亦稱頻率分布直方圖。統計學中表示頻率分布的圖形。在直角坐標系中,用橫軸表示隨機變數的取值,橫軸上的每個小區間對應一個組的組距,...
各組樣本數據的個數稱為頻數,頻數除以樣本總個數為頻率)的值,以頻率和組距的商為高、組距為底的矩形在直角坐標繫上來表示,由此畫成的統計圖叫做頻率分布直方圖...
頻率分布,是指在統計分組的基礎上,將總體中各單位按組歸類整理,按一定順序排列,形成的總體中各單位在各組間的分布。其實質是,在各組按順序排列的基礎上,列出...
次數直方圖(frequency histogram) 一譯“頻數直方圖”。是直方圖的一種。做法如下:(1)將數據分組,確定各組組限;(2)以各組的上、下限之間線段為寬,以該組數據...
在相同的條件下,進行了n次試驗,在這n次試驗中,事件A發生的次數m稱為事件A發生的頻數。比值m/n稱為事件A發生的頻率,用文字表示定義為:每個對象出現的次數與總...
直方圖(Histogram),又稱質量分布圖,是一種統計報告圖,由一系列高度不等的縱向條紋或線段表示數據分布的情況。 一般用橫軸表示數據類型,縱軸表示分布情況。直方圖是...
灰度直方圖是關於灰度級分布的函式,是對圖像中灰度級分布的統計。灰度直方圖是將數字圖像中的所有像素,按照灰度值的大小,統計其出現的頻率。灰度直方圖是灰度級的函式...
血細胞直方圖是反映血細胞體積大小的頻率分布圖。...... 是反映PLT體積大小分布頻率的分布圖,正常PLT直方圖呈左偏態分布,峰值一般在6-10fl之間,直方圖左移,提示PLT...
直方圖平坦化是將一已知灰度機率密度分布的圖像,經過某種變換,變成一幅具有均勻灰度機率密度分布的新圖像,其結果是擴展了像元取值的動態範圍,從而達到增強圖像整體對比...
顏色直方圖是在許多圖像檢索系統中被廣泛採用的顏色特徵。它所描述的是不同色彩在整幅圖像中所占的比例,而並不關心每種色彩所處的空間位置,即無法描述圖像中的...
通過改變和調整圖像的灰度直方圖,改變圖像值的分布和結構關係的反差增強方法。...... 圖像直方圖表達的是離散圖像值的機率密度函式,反映的是圖像像元值分布的相對頻率...
通過長方形的高代表對應組的頻數與組距的比(因為組距是一個常數,為了畫圖和看圖方便,通常直接用高表示頻數),這樣的統計圖稱為頻數分布直方圖.它能:①清楚顯示各組...
失效數據直方圖,屬於學科專有名詞。...... 失效數據直方圖,屬於學科專有名詞。中文名稱 失效數據直方圖 ...得到每一小組上下限組距內數據出現的頻率,以頻率為縱坐標,...
詞目: 直方圖正態化。 英文: histogram normalization。 釋文: 使圖像的直方圖呈常態分配和近似常態分配。相當於高斯擴展。正態化使直方圖中頻率高處的反差即圖像...
次數分布圖(freguency distribution chart),統計圖的一種。用統計圖的形式展示一組數據的次數(頻數)分布情況的圖形。常見的有次數分布直方圖(簡稱次數直方圖)、次數...
頻率多邊形也是顯示累積頻率分布的好選擇。要創建一個頻率多邊形,就像直方圖一樣,選擇一個類間隔。然後繪製一個代表數據中分數值的X軸。用一個刻度標記標記每個班級...
灰度直方圖是關於灰度級分布的函式,是對圖像中灰度級分布的統計。灰度直方圖是將數字圖像中的所有像素,按照灰度值的大小,統計其出現的頻率。灰度直方圖是灰度級的函式...
