頻數多邊形（frequency polygon）是用組織圖來造成的同組織圖一樣是來表達這些數據的整體規律或趨勢，從而分析這些數據的分布情況。折線圖的兩個終點要與橫軸相交，具體的做法是將第一個矩形的頂部中點通過豎邊中點(即該組頻數一半的位置)連線到橫軸，最後一個矩形頂部中點與其豎邊中點連線到橫軸。這樣才會使折線圖下所圍成的面積與直方圖的面積相等，從而使二者所表示頻數一致。
基本介紹
- 中文名：頻數多邊形
- 外文名：frequency polygon
- 組成：組織圖
- 內容：表達這些數據的整體規律或趨勢
- 學科：數理科學
- 用途：分析數據分布情況
繪製方法,示例,注意事項,
繪製方法
在直方圖的基礎上，把直方圖頂部的中點（即組中值）用直線連線起來，再把原來的直方圖抹掉就是頻數多邊形圖。
頻率多邊形是用於理解分布形狀的圖形設備。它們與直方圖具有相同的用途，但對於比較數據集特別有用。頻率多邊形也是顯示累積頻率分布的好選擇。
要創建一個頻率多邊形，就像直方圖一樣，選擇一個類間隔。然後繪製一個代表數據中分數值的X軸。用一個刻度標記標記每個班級間隔的中間，並用該班級表示的中間值標記它。繪製Y軸以指示每個班級的頻率。在每個班級間隔的中間放置一個與其頻率相對應高度的點。最後，連線點。您應該在數據中包含一個低於最低值的等級間隔，並且在最高值之上包含一個等級間隔。然後圖形將觸碰兩側的X軸。
示例
表1.心理測試成績的頻率分布。
| 下限 | 上限 | 計數 | 累計計數 |
|---|---|---|---|
29.5 | 39.5 | 0 | 0 |
39.5 | 49.5 | 3 | 3 |
49.5 | 59.5 | 10 | 13 |
59.5 | 69.5 | 53 | 66 |
69.5 | 79.5 | 107 | 173 |
79.5 | 89.5 | 147 | 320 |
89.5 | 99.5 | 130 | 450 |
99.5 | 109.5 | 78 | 528 |
109.5 | 119.5 | 59 | 587 |
119.5 | 129.5 | 36 | 623 |
129.5 | 139.5 | 11 | 634 |
139.5 | 149.5 | 6 | 640 |
149.5 | 159.5 | 1 | 641 |
159.5 | 169.5 | 1 | 642 |
169.5 | 179.5 | 0 | 642 |
圖1所示的642個心理測試分數的頻數多邊形由表1所示的頻數表構成。
X軸上的第一個標籤是35.這代表從29.5延伸到39.5的間隔。由於最低測試得分為46，因此該區間的頻率為0.標記為45的點表示從39.5到49.5的區間。這個區間有三個分數。圍繞85分的區間有147分。
可以很容易地從圖1中辨別出分布的形狀。大多數分數在65到115之間。顯然，分布並不是對稱的，因為良好的分數（右邊）比差分更慢地左邊），分布是傾斜的。
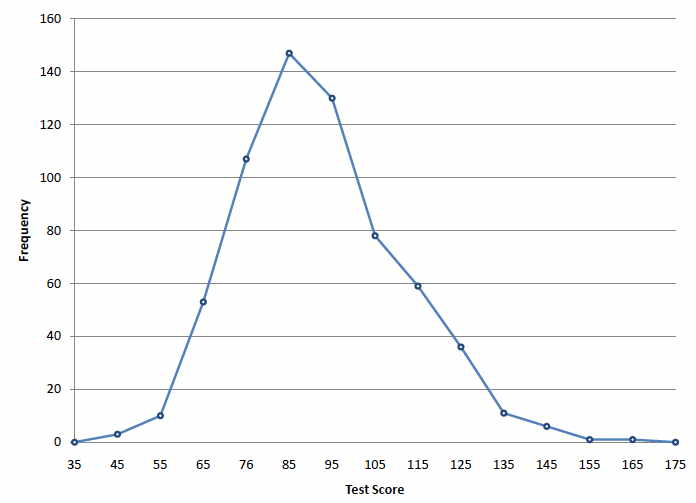圖1 心理測試分數的頻率多邊形累積頻率多邊形對於相同的測試分數示於圖2的曲線是相同的，除了每個點的Y值是學生在對應的類間隔的數目之前加在較低層段的所有數字。例如，在標有“35”的區間中沒有得分，在區間“45”中有三個，在區間“55”中沒有得分。因此，對應於“55”的Y值為13.由於642名學生參加了測試，最後一個時間段的累積頻率是642。
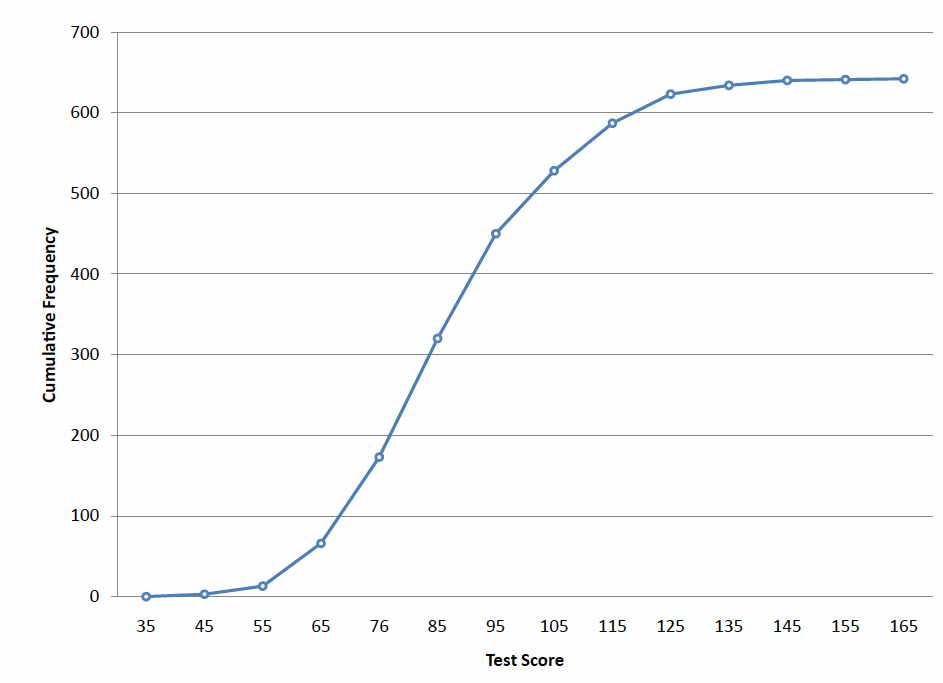圖2 心理測試分數的累計頻率多邊形頻數多邊形可用於比較分布。這是通過疊加為不同數據集繪製的頻數多邊形來實現的。圖3提供了一個例子。數據來自一項任務，其目標是儘可能快地將計算機游標移動到螢幕上的目標。在20個試驗中，目標是一個小矩形;在另外20個，目標是一個大矩形。在每次試驗中記錄達到目標的時間。這兩個分布（每個目標一個）在圖3中繪製在一起。該圖顯示雖然在時間上有一些重疊，但是將游標移動到小目標通常需要較長的時間。
圖3 疊加的頻率多邊形
圖4 疊加的累積頻率多邊形