VC維(外文名Vapnik-Chervonenkis Dimension)的概念是為了研究學習過程一致收斂的速度和推廣性,由統計學理論定義的有關函式集學習性能的一個重要指標。
基本介紹
- 中文名:vc維
- 外文名:Vapnik-Chervonenkis Dimension
- 目的:為了研究學習過程一致收斂
- 原理:統計學理論
定義,感知器的VC維,理解VC維,
定義
傳統的定義是:對一個指示函式集,如果存在H個樣本能夠被函式集中的函式按所有可能的2的H次方種形式分開,則稱函式集能夠把H個樣本打散;函式集的VC維就是它能打散的最大樣本數目H。若對任意數目的樣本都有函式能將它們打散,則函式集的VC維是無窮大,有界實函式的VC維可以通過用一定的閾值將它轉化成指示函式來定義。
VC維反映了函式集的學習能力,VC維越大則學習機器越複雜(容量越大),遺憾的是,尚沒有通用的關於任意函式集VC維計算的理論,只對一些特殊的函式集知道其VC維。例如在N維空間中線性分類器和線性實函式的VC維是N+1。
如果一個假設空間存在突破點,則一定存在成長函式 被某個上限函式B(N,k)所約束,而上限函式等於一個組合的求和形式
被某個上限函式B(N,k)所約束,而上限函式等於一個組合的求和形式 ,易知該形式的最高次項是
,易知該形式的最高次項是 。圖左和右分別是以上限函式為上限的情況和以為
。圖左和右分別是以上限函式為上限的情況和以為 上限的情況。
上限的情況。




 圖1
圖1可以得出:

如果輸入數據量N(或者用k表示)大於VC維,則有k一定是假設空間H的突破點。
在N≥2, 時,可得:
時,可得:


一個有限的VC維總是能夠保證尋找到的近似假設g是泛化的,即近似假設g滿足 。沒有必要知道具體的VC維的值,只需要知道它是有限的就可以得出這一結論。
。沒有必要知道具體的VC維的值,只需要知道它是有限的就可以得出這一結論。

同時這一結論與下述部分沒有關係:1.使用的算法,即使使用某種算法使得 很大,也依然能滿足上述的性質;2.輸入數據的分布P;3.未知的目標函式f。
很大,也依然能滿足上述的性質;2.輸入數據的分布P;3.未知的目標函式f。

即VC維可應對任意的假設空間,任意的數據分布情況,任意的目標函式。滿足這一性質可以得到如圖所示的流程圖,其中灰色的部分表示上述幾個不會影響 這一結果的部分:
這一結果的部分:

 圖2
圖2- 對於假設集合,這是一個由人工產生的集合,而VC維會告訴我們哪一個可以泛化,而哪一些不行。
- 對於數據集,VC維只能用一種機率性的說法解釋,它只能告訴你在高機率下可以泛化;而如果恰好用了一個非常不好的數據集,就沒有必要去對其進行泛化。
感知器的VC維
以下兩個條件保證了2維線性可分的數據是可以學習的:
1.線性可分的數據通過PLA算法運行足夠長的時間(T步驟足夠大),則會找出一條可以正確分類的直線,使得樣本中沒有產生分錯類的情況,即 ;
;

2.在訓練樣本和整個數據集都服從同一分布P的前提下,有VC限制保證了,在 且訓練樣本N足夠大時,
且訓練樣本N足夠大時, 。
。


由VC維的定義知:只要求出 是一個有限數,則可以使用VC限制來保證
是一個有限數,則可以使用VC限制來保證 。那么在維數大於二維時,感知器的dvc能否表示成一個有限數。已知,1維感知器的VC維:
。那么在維數大於二維時,感知器的dvc能否表示成一個有限數。已知,1維感知器的VC維: =2;2維感知器的VC維:
=2;2維感知器的VC維: =3。猜想,d維感知器的VC維:
=3。猜想,d維感知器的VC維: =d+1。
=d+1。





證明:1. ≥d+1
≥d+1

取出N=d+1個在 的樣本點,得到了如下的可逆矩陣(滿秩矩陣):
的樣本點,得到了如下的可逆矩陣(滿秩矩陣):

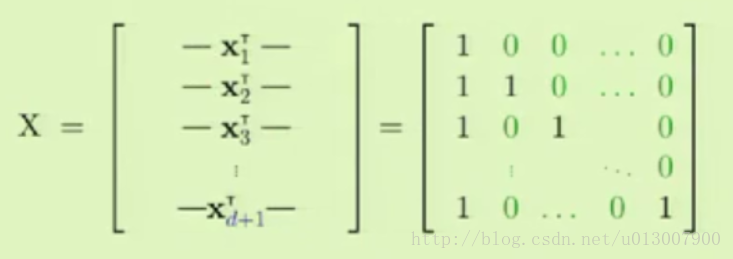 可逆矩陣
可逆矩陣對於任意的 ,我們需要找到一個向量
,我們需要找到一個向量 ,且
,且 滿足sign(X
滿足sign(X )=y。
)=y。




因為y向量可以是任意一種形式的二分類,如果我們能夠對任意一個y向量都能找到對應的 ,那么我們就可以得到所有的二分類,即實現完全二分類。令讓X
,那么我們就可以得到所有的二分類,即實現完全二分類。令讓X =y。同時因為X是可逆的,我們得到
=y。同時因為X是可逆的,我們得到 =X−1y,因此我們可以解得
=X−1y,因此我們可以解得 的值。
的值。




因此我們證明了 ≥d+1。
≥d+1。

2. ≤d+1
≤d+1

對於任意d+2個樣本點,X1,X2,…,Xd+1,Xd+2的維度均為d+1。那么當維度大於點的個數的時候,可以知道他們一定線性相關,即 ,其中不是所有的
,其中不是所有的 都為0(因為任意xj的第一維都是1,所以權重
都為0(因為任意xj的第一維都是1,所以權重 不可能全是0)。
不可能全是0)。



構造一組 ,且對於Xj,讓yj=−1,其餘權重為零的Xi對應的yi可以任意取值。
,且對於Xj,讓yj=−1,其餘權重為零的Xi對應的yi可以任意取值。


令 ,那么對於每一個非零的ai,可以得到
,那么對於每一個非零的ai,可以得到 和(ai)的符號是相同的,即,
和(ai)的符號是相同的,即, 。
。



因此 (因為ai=0時,累加無效),同時可得
(因為ai=0時,累加無效),同時可得 >0。則可以得到
>0。則可以得到



假設不成立,因此在任何d+2個輸入數據集中必然都存在不能滿足的二分類,即 。
。

證明了 。
。

理解VC維
如果從假設空間的數量|H|角度上描述,則自由度是無限大的;但是從感知器在二元分類上這一限制條件入手,則可以使用VC維作為自由度的衡量。
VC維和假設空間參數之間的關係:
當dvc=1時,假設空間有1個參數,即閾值。
 dvc=1
dvc=1當dvc=2時,假設空間有2個參數,即左右邊界點。因此在大部分情況下,dvc大致等於假設空間參數的個數。
 dvc=2
dvc=2將一個1D的感知器輸出連線到下一個1D感知器的輸入,如下圖所示,這樣就得到了8個參數,然而它的自由度並沒有增加。根據dvc,我們可以得出只需要一個感知器就足夠的結論。
 1D感知器輸入
1D感知器輸入
