基本介紹
- 中文名：KMP算法
- 外文名：The Knuth-Morris-Pratt Algorithm
- 輸入：正文串T[1,n]和模式串W[1,m]
- 輸出：匹配結果match[1,n]
- 發現者：D.E.Knuth等
- 時間複雜度：O（m+n）
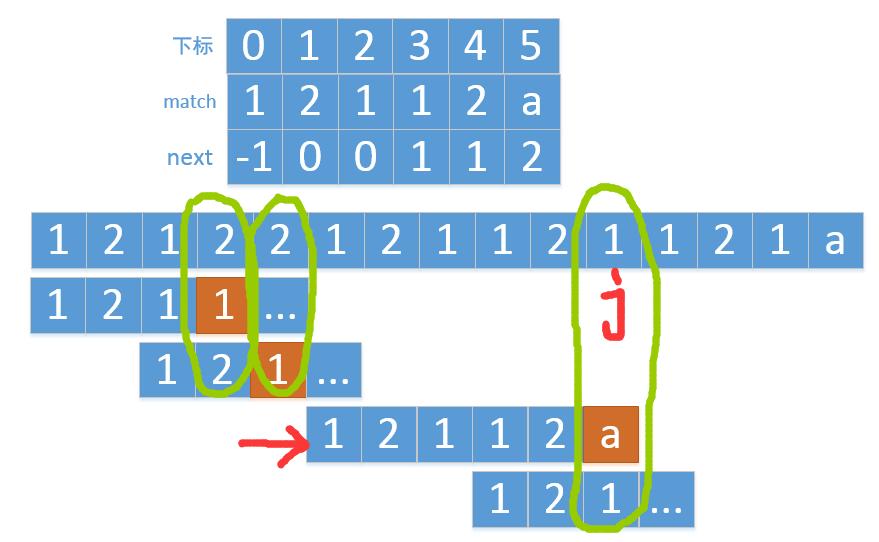
基本思想,串匹配算法,next和newnext,BM串匹配,d函式,RK串匹配,最佳化,最佳化思路,C++ 原始碼,Pascal 原始碼,
基本思想
設主串（下文中我們稱作T）為：a b a c a a b a c a b a c a b a a b b
模式串（下文中我們稱作W）為：a b a c a b
用暴力算法匹配字元串過程中，我們會把T[0] 跟 W[0] 匹配，如果相同則匹配下一個字元，直到出現不相同的情況，此時我們會丟棄前面的匹配信息，然後把T[1] 跟 W[0]匹配，循環進行，直到主串結束，或者出現匹配成功的情況。這種丟棄前面的匹配信息的方法，極大地降低了匹配效率。
而在KMP算法中，對於每一個模式串我們會事先計算出模式串的內部匹配信息，在匹配失敗時最大的移動模式串，以減少匹配次數。
在第一次匹配過程中
T: a b a c a a b a c a b a c a b a a b b
W: a b a c a b
在T[5]與W[5]出現了不匹配，而T[0]~T[4]是匹配的，現在T[0]~T[4]就是上文中說的已經匹配的模式串子串，現在移動找出最長的相同的前綴和後綴並使他們重疊：
T: a b a c aa b a c a b a c a b a a b b
W: a b a c a b
然後在從上次匹配失敗的地方進行匹配，這樣就減少了匹配次數，增加了效率。
然而，如果每次都要計算最長的相同的前綴反而會浪費時間，所以對於模式串來說，我們會提前計算出每個匹配失敗的位置應該移動的距離，花費的時間就成了常數時間。比如：
j | 0 | 1 | 2 | 3 | 4 | 5 |
W[j] | a | b | a | c | a | b |
F(j) | 0 | 0 | 1 | 0 | 1 | 2 |
當W[j]與T[j]不匹配的時候，設定j = F(j-1).
文獻中，朱洪對KMP算法作了修改，他修改了KMP算法中的next函式，即求next函式時不但要求W[1,next(j)-1]=W[j-(next(j)-1)，j-1]，而且要求W[next(j)]<>W[j]，他記修改後的next函式為newnext。顯然在模式串字元重複高的情況下，朱洪的KMP算法比KMP算法更加有效。
以下給出朱洪的改進KMP算法和next函式和newnext函式的計算算法。
串匹配算法
輸入： 正文串T[1,n]和模式串W[1,m]
輸出： 匹配結果match[1,n]
int KMP(string W,string T){ int i=1,j=1; while(i<=n){ while (j!=0&&W[j]!=T[i]) j=next[j]; if(j==m) return i-m+1;//匹配成功，返回匹配位置s else{j++; i++;} } return -1;//匹配失敗}procedureKMP begin i=1 j=1 while i<=n do while j<>0 and W[j]<>T[i] do j=newnext[j] endwhile if j=m return "success" else j++ i++ endif endwhile return "failure"end
next和newnext
輸入： 模式串W[1,m]
輸出： next[1,m+1]和newnext[1,m]
void getNext(string W){ for(int i=1; i<m; i++){ int j=i; while(j>0){ j=next[j]; if(W[j]==W[i]){ next[i+1]=j+1; break; } } }}function NEXT begin next[1]=newnext[1]=0 j=2 while j<=m do i=next[j-1] while i<>0 and W[i]<>W[j-1]) do i=next[i] endwhile next[j]=i+1 j=j+1 endwhile endfunction NEWNEXT begin newnext[1]=0 j=2 while j<=m do i=next(j) if i=0 or W[j]<>W[i+1] newnext[j]=i else newnext[j]=newnext[i] endif j++ endwhile end
更加簡潔的算法
下面是更加簡潔的算法：
void GetNext(charT[],intnext[]){ next[1]=0; j=1;k=0; while(j<=strlen(T)) //此處應包含string頭檔案 if((k==0)||(T[j]==T[k])){ next[j]=k; j++; k++; } else k=next[k];}計算過程
假設在執行正文中自位置 i 起“返前”的一段與模式的自右至左的匹配檢查中，一旦發現不匹配（不管在什麼位置），則去執行由W[m]與t[i]+d(x）起始的自右至左的匹配檢查，這裡x是字元t。它的效果相當於把模式向右滑過d(ti）一段距離。顯然，若ti不在模式中出現或僅僅在模式末端出現，則模式向右滑過的最大的一段距離m。圖1.1示出了執行BM算法時的各種情況。實線連線發現不匹配以後要進行比較的正文和模式中的字母，虛線連線BM算法在模式向右滑後正文和模式中應對齊的字母，星號表示正文中的一個字母。
圖1.1：執行BM算法時的各種情況
BM算法由算法1.3給出，函式d的算法由算法1.4給出。計算函式d的時耗顯然是Θ（m）。BM算法的最壞情況時耗是Θ（mn）。但由於在實用中這種情況極少出現，因此BM算法仍廣泛使用。
BM串匹配
輸入： 正文串W[1,m]和模式串T[1,n]
輸出： 匹配結果match[1,n]
procedure BM begin i=m Repeat j=m k=i while(j>0)and(w[j]=t[k])do j=j-1 k=k-1 endwhile i=i+d[t[i]] Until(j=0)or(i>n) If j=0 return "SUCCESS" else return“FAILURE” endif end
d函式
functiond:integer;beginforx∈∑dod(x)=mforj=m-1downto1doifd(w[j])=md(w[j]):=m-jendforendxi+1=ord(ti+1）dm-1+ord(ti+2）dm-2+…+ord(ti+m)=(xi-ord(ti)dm-1）.d+ord(ti+m)
因此有 h(xi+1）=((h(xi)-x·ord(ti））·d+ord(ti+m)mod q ，i=1,2，……，n-m
RK串匹配
programRK;begin{計算x,x:=d↑（m-1）modq}x=1fori=1tom-1dox=（32*x)modq{計算模式W的散列函式值}s=0fori=1tomdos=((s*32）+ord(w[i]))modq{計算正文T的第一個長度為m的字元段的散列函式值}t=0fori=1tomdot=(t*32+ord(w[i]))modq{如果正文的第一個長度為m的字元段和模式有相同的散列函式值，則進行匹配檢查.否則，以及在匹配檢查失敗情況下，繼續計算下一個字元段的散列函式值}i=1whilei<=n-mdoifs=t{進行匹配檢查}k=1j=iwhile(t[j]=w[k])and(k<=m)doj=j+1k=k+1endwhileifi<n-m{計算下一字元段的散列函式值}t=((t-x*ord(t[i]))*32+ord(t[i+m]))modqi=i+1endifendifendwhilereturn“FAILURE”end顯然，如果不計執行匹配檢查的時間，則RK算法的剩餘部分執行時間是Θ（m+n)。不過，如果計及執行匹配檢查的時間，則在理論上，RK算法需要時耗Θ（mn）。但是，我們總可設法取q適當大，使得mod函式在計算機中仍可執行而衝突（即不同的字元串具有相同的散列值）又極小可能發生，而使算法的實際執行時間只需Θ（m+n）。
BM算法
BM算法和KMP算法的差別是對模式串的掃描方式自左至右變成自右至左。另一個差別是考慮正文中可能出現的字元在模式中的位置。這樣做的好處是當正文中出現模式中沒有的字元時就可以將模式大幅度滑過正文。
BM算法的關鍵是根據給定的模式W[1,m]，，定義一個函式d: x->{1,2，…，m},這裡x∈∑。函式d給出了正文中可能出現的字元在模式中的位置。
最佳化
最佳化思路
KMP算法是可以被進一步最佳化的。
我們以一個例子來說明。譬如我們給的P字元串是“abcdaabcab”，經過KMP算法，應當得到“特徵向量”如下表所示：
下標i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
p(i) | a | b | c | d | a | a | b | c | a | b |
next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 | 1 |
但是，如果此時發現p(i) == p(k），那么應當將相應的next[i]的值更改為next[k]的值。經過最佳化後可以得到下面的表格：
下標i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
p(i) | a | b | c | d | a | a | b | c | a | b |
next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 | 1 |
最佳化的next[i] | -1 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 3 | 0 |
（1）next[0]= -1 意義：任何串的第一個字元的模式值規定為-1。
（2）next[j]= -1 意義：模式串T中下標為j的字元，如果與首字元相同，且j的前面的1—k個字元與開頭的1—k個字元不等（或者相等但T[k]==T[j]）（1≤k<j），如：T=”abCabCad” 則 next[6]=-1，因T[3]=T[6].
（3）next[j]=k 意義：模式串T中下標為j的字元，如果j的前面k個字元與開頭的k個字元相等，且T[j] != T[k] （1≤k<j）即T[0]T[1]T[2]......T[k-1]==T[j-k]T[j-k+1]T[j-k+2]…T[j-1]且T[j] != T[k].（1≤k<j）;
(4) next[j]=0 意義：除（1）（2）（3）的其他情況。
補充一個next[]生成代碼：
void getNext(const char*pattern,int next[]){ next[0]=-1; int k=-1,j=0; while(pattern[j]!='\0'){ while (k!=-1 && pattern[k]!=pattern[j]) k=next[k]; ++j; ++k; if(pattern[k]==pattern[j]) next[j]=next[k]; else next[j]=k; } }C++ 原始碼
KMP算法查找串S中含串P的個數count
#include<iostream>#include<stdlib.h>#include<vector>using namespace std;inline void NEXT(const string&T, vector<int>&next){//按模式串生成vector,next(T.size()) next[0] = -1; for (int i = 1; i<T.size(); i++){ int j = next[i - 1]; while (j >= 0 && T[i - 1] != T[j]) j = next[j];//遞推計算 if (j >= 0 && T[i - 1] == T[j]) next[i] = j + 1; else next[i] = 0; }}inline string::size_type COUNT_KMP(const string&S, const string&T){ //利用模式串T的next函式求T在主串S中的個數count的KMP算法 //其中T非空， vector<int>next(T.size()); NEXT(T, next); string::size_type index, count = 0; for (index = 0; index<S.size(); ++index){ int pos = 0; string::size_type iter = index; while (pos<T.size() && iter<S.size()){ if (S[iter] == T[pos]){ ++iter; ++pos; } else{ if (pos == 0) ++iter; else pos = next[pos - 1] + 1; } } if (pos == T.size() && (iter - index) == T.size()) ++count; } return count;}int main(int argc, char*argv[]){ string S="abaabcacabaabcacabaabcacabaabcacabaabcac"; string T="ab"; //cin >> S; //cin >> T; string::size_type count = COUNT_KMP(S, T); cout << count << endl; system("PAUSE"); return 0;}Pascal 原始碼
const MAX_STRLEN=255;var next:array[1..MAX_STRLEN] of longint; str_s,str_t:string; int_i:longint;procedure get_next(t:string); var j,k:longint; begin j:=1; k:=0; while j<length(t) do begin if (k=0) or (t[j]=t[k]) then begin inc(j); inc(k); next[j]:=k; end else k:=next[k]; end; end;function kmp(s,t:string):longint; var i,j,back:longint; begin get_next(t); back:=0; i:=1; j:=1; while (i<=length(s)) and (j<=length(t)) do begin if (j=0) or (s[i]=t[j]) then begin inc(i); inc(j); end else j:=next[j]; if j>length(t) then back:=i-length(t); end; exit(back); end;begin write('S='); readln(str_s); write('T='); readln(str_t); int_i:=kmp(str_s,str_t); if int_i<>0 then writeln('Found ',str_t,' in ',str_s,' at ',int_i,'.') else writeln('Cannot found ',str_t,' in ',str_s,'.')end.kmp函式用於模式匹配，str_t是模式串，str_s是原串。返回模式串的位置，找不到則返回0。
