在用於查找子字元串的算法當中,BM(Boyer-Moore)算法是目前被認為最高效的字元串搜尋算法,它由Bob Boyer和J Strother Moore設計於1977年。 一般情況下,比KMP算法快3-5倍。該算法常用於文本編輯器中的搜尋匹配功能,比如大家所熟知的GNU grep命令使用的就是該算法,這也是GNU grep比BSD grep快的一個重要原因。
基本介紹
- 中文名:博伊爾-摩爾算法
- 外文名:Boyer-Moore Algorithm
- 提出者: Bob Boyer和J Strother Moore
- 提出時間:1977年
- 套用學科:計算機科學
- 適用領域範圍:字元串搜尋
主要特徵
算法基本思想
j = 0;while (j <= (strlen(text)-strlen(pattern))){ for (i = 0; i < strlen(pattern) && pattern[i] == text[i+j]; ++i); if (i == strlen(pattern)) { Match; break; } else ++j; }j = 0;while(j <= (strlen(text)-strlen(pattern))){ for (i = strlen(pattern); i >= 0 && pattern[i] == text[i + j]; --i); if (i < 0)) { Match; break; } else j += BM(); }字元風暴
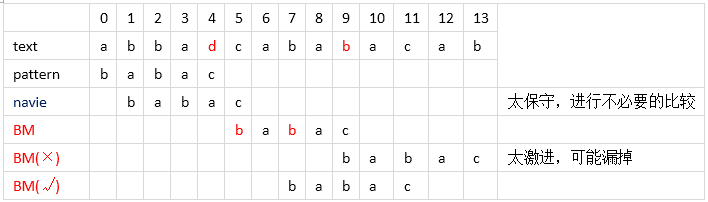
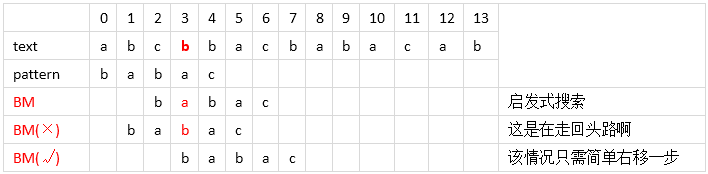
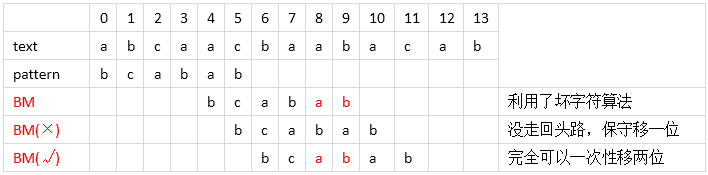
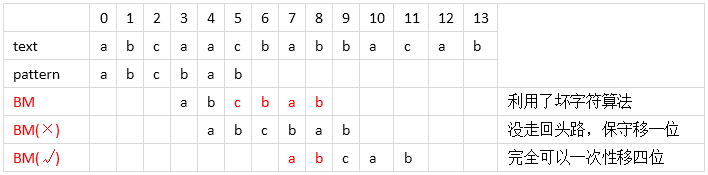
理論探討
壞字元算法

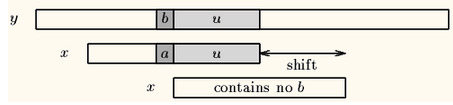
好後綴算法


移動規則
具體執行
壞字元bmBc[]
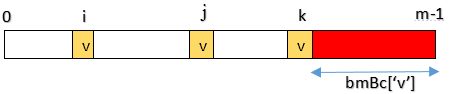
void PreBmBc(char *pattern, int m, int bmBc[]){ int i; for (i = 0; i < MAX_CHAR; i++) bmBc[i] = m; for (i = 0; i < m - 1; i++) bmBc[pattern[i]] = m - 1 - i; /* printf(""bmBc[]:); for (i = 0; i < m; i++) printf("%d ",bmBc[pattern[i]]); printf("\n"); */}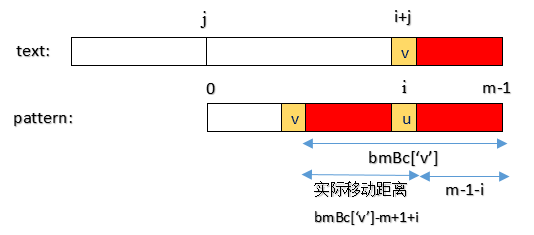
好後綴bmGs[]



void PreBmGs(char *pattern, int m, int bmGs[]){ int i, j; int suff[SIZE]; // 計算後綴數組 suffix(pattern, m, suff); // 先全部賦值為m,包含Case3 for (i = 0; i < m; i++) bmGs[i] = m; // Case2 j = 0; for (i = m - 1; i >= 0; i--) { if (i + 1 == suff[i]) { for (;j < m - 1 - i; j++) { if (m == bmGs[j]) bmGs[j] = m - 1 - i; } } } // Case1 for (i = 0; i <= m - 2; i++) bmGs[m - 1 - suff[i]] = m - 1 - i; print(bmGs, m , "bmGs[]");}計算suff[]
pattern: b c a b a b a b
void suffix_old(char *pattern, int m, int suff[]){ int i, j; suff[m - 1] = m; for (i = m - 2; i >= 0; i--) { j = i; while (j >= 0 && pattern[j] == pattern[m -1 - i + j]) j--; suff[i] = i - j; }}
pattern:a a a a a b a a a a
void suffix(char *pattern, int m, int suff[]){ int f, g, i; suff[m - 1] = m; g = m - 1; for (i = m - 2; i >= 0; --i) { if (i > g && suff[i + m - 1 - f] < i - g) suff[i] = suff[i + m - 1 - f]; else { if (i < g) g = i; f = i; while (g >= 0 && pattern[g] == pattern[g + m - 1 - f]) --g; suff[i] = f - g; } } //print(suff, m, "suff[]");}完整C代碼
#include <stdio.h>#include <string.h>#define MAX_CHAR 256#define SIZE 256#define MAX(x, y) (x) > (y) ? (x) : (y)void BoyerMoore(char *pattern, int m, char *text, int n);int main(){ char text[256], pattern[256]; while (1) { puts("Please input the text and the pattern:(input Q to quit.)"); gets(text); if (!strcmp(text, "Q") || ! strcmp(text, "q")) break; gets(pattern); //printf("%s\n", text); //printf("%s\n", pattern); BoyerMoore(pattern, strlen(pattern), text, strlen(text)); printf("\n"); } return 0;}void print(int *array, int n, char *arrayName){ int i; printf("%s:", arrayName); for (i = 0; i < n; i++) printf("%d ", array[i]); printf("\n");}void PreBmBc(char *pattern, int m, int bmBc[]){ int i; for (i = 0; i < MAX_CHAR; i++) bmBc[i] = m; for (i = 0; i < m - 1; i++) bmBc[pattern[i]] = m - 1 - i; /* printf(""bmBc[]:); for (i = 0; i < m; i++) printf("%d ",bmBc[pattern[i]]); printf("\n"); */}void suffix_old(char *pattern, int m, int suff[]){ int i, j; suff[m - 1] = m; for (i = m - 2; i >= 0; i--) { j = i; while (j >= 0 && pattern[j] == pattern[m -1 - i + j]) j--; suff[i] = i - j; }}void suffix(char *pattern, int m, int suff[]) //改進計算suffix方法{ int f, g, i; suff[m - 1] = m; g = m - 1; for (i = m - 2; i >= 0; --i) { if (i > g && suff[i + m - 1 - f] < i - g) suff[i] = suff[i + m - 1 - f]; else { if (i < g) g = i; f = i; while (g >= 0 && pattern[g] == pattern[g + m - 1 - f]) --g; suff[i] = f - g; } } //print(suff, m, "suff[]");}void PreBmGs(char *pattern, int m, int bmGs[]){ int i, j; int suff[SIZE]; // 計算後綴數組 suffix(pattern, m, suff); // 先全部賦值為m,包含Case3 for (i = 0; i < m; i++) bmGs[i] = m; // Case2 j = 0; for (i = m - 1; i >= 0; i--) { if (i + 1 == suff[i]) { for (;j < m - 1 - i; j++) { if (m == bmGs[j]) bmGs[j] = m - 1 - i; } } } // Case1 for (i = 0; i <= m - 2; i++) bmGs[m - 1 - suff[i]] = m - 1 - i; print(bmGs, m , "bmGs[]");}void BoyerMoore(char *pattern, int m, char *text, int n){ int i, j, bmBc[MAX_CHAR], bmGs[SIZE]; // Preprocessing PreBmBc(pattern, m, bmBc); PreBmGs(pattern, m, bmGs); // Searching j = 0; while (j <= n - m) { for (i = m - 1; i >= 0 && pattern[i] == text[i + j]; i--); if (i < 0) { printf("Find it, the position is %d\n", j); j += bmGs[0]; return ; } else j += MAX(bmBc[text[i + j]] - m + 1 + i, bmGs[i]); } printf("No find.\n");}