基本介紹
定義,偽代碼,Python代碼,詳細闡述,next數組的理解與計算,C示例代碼,C示例改進過程,實際套用,摘要,關鍵字,提出問題,問題描述,結束語,
定義
一種由Knuth(D.E.Knuth)、Morris(J.H.Morris）和Pratt(V.R.Pratt）三人設計的線性時間字元串匹配算法。這個算法不用計算變遷函式δ，匹配時間為Θ（n），只用到輔助函式π[1，m]，它是在Θ（m）時間內，根據模式預先計算出來的。數組π使得我們可以按需要，“現場”有效的計算（在平攤意義上來說）變遷函式δ。粗略地說，對任意狀態q=0，1，…，m和任意字元a∈Σ，π[q]的值包含了與a無關但在計算δ（q，a）時需要的信息。由於數組π只有m個元素，而δ有Θ（m∣Σ∣）個值，所以通過預先計算π而不是δ，使得時間減少了一個Σ因子。
偽代碼
KMP-MATCHER(T，P)n←length[T]m←length[P]π←COMPUTE-PREFIX-FUNCTION(P)q←0 //Numberofcharactersmatched.fori←1ton //Scanthetextfromlefttoright.dowhileq>0andP[q+1]≠T[i]doq←π[q] //Nextcharacterdoesnotmatch.ifP[q+1]=T[i]thenq←q+1 //Nextcharactermatches.ifq=m //IsallofPmatched?thenprint"Patternoccurswithshift"i-mq←π[q] //Lookforthenextmatch.COMPUTE-PERFIX-FUNCTION(P)m←length[P]π[1]←0k←0forq←2tomdowhilek>0andP[k+1]≠P[q]dok←π[k]ifP[k+1]=P[q]thenk←k+1π[q]←kreturnπ
Python代碼
defprefix(str):m=len(str)pi=[0foriinrange(m)]pi[0]=0k=0forqinrange(1,m):whilek>0andstr[k]!=str[q]:k=pi[k-1]ifstr[k]==str[q]:k=k+1pi[q]=kreturnpidefmatch(t,p):n=len(t)m=len(p)pi=prefix(p)q=0foriinrange(0,n):whileq>0andp[q]!=t[i]:q=pi[q-1]ifp[q]==t[i]:q=q+1ifq==m:print("matchedin%d.\n"%(i-m+1))print("notmatched!\n")詳細闡述
next數組的理解與計算
首先聲明在不同的地方對next數組的定義和計算有所不同，為了避免混淆，在此僅介紹一種。
next數組是對於模式字元串也就是需要被匹配字元串其中的每一個字母而言，為了在匹配時避免重複判斷而存在，下面通過一個實例來介紹next數組的意義和具體用法。
首先擺出next數組
a 匹配串：b a b a b b；
0 0 1 2 3 1；
列如 s原串：b a b a b a b c b a b a b a b a b b；
a匹配串：b a b a b b；
先按暴力匹配可以得到如下
原串：b a b a b a bcb a b a b a b a b b；
匹配串 b a bab b；
在如圖黑色字母處出現不匹配，如果繼續暴力，則會將匹配串向後移一位，然後再重新將匹配串的指針指向首位重新開始逐個匹配。但現在思考一下，我已經匹配了過了前三個字元了，可不可以合理地利用已知的條件呢？
next數組就起到了運用已知條件的作用。如next[2]=1（從0開始），代表從匹配串隊首開始向後走1（包括此點）與從a[2]開始向前走1的字元串完全相同。如next[3]=2,代表a[0],a[1]所組成的字元串與a[2]a[3]組成的完全相同。next[n]就代表n滿足上述條件的長度。
這樣的話next數組的求解就十分容易了，只需o（n）的複雜度；next[0]必為0，對於求解next[n]，採用遞推思想，如果next[n]=k;(k>0)則必須next[n-1]=k-1;如果next[n-1]=0;則看next[n]是否等於next[0]。如等於則next[n]=1。
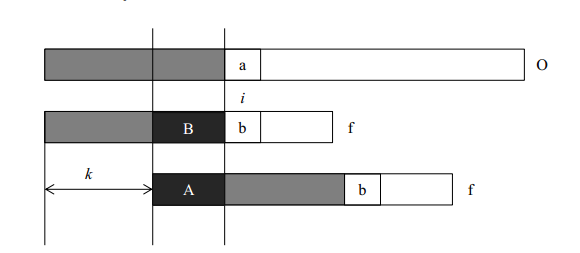
接下來就是實現時next數組的現實作用了，如上圖，設原串的指針為i，匹配串的指針為j。當匹配到a[3]失敗時，要注意因為從a[j]即a[3]開始向前走next[j-1]，即1與從隊首開始向後走next[j-1]的字元是相同的，所以j回到next[j-1]，即a[1]的位置，而i指針不變，再進行比較。這樣就能高效地進行匹配。
結合圖像來看，如右下圖加黑的B與A部分就是匹配失敗時next[j-1]的值代表B部分與A部分完全相同，所以直接跳過這部分，直接將j指針移到A部分的後一位處，即next[j-1]處。
C示例代碼
//c++實現的KMP算法，所有涉及字元串，其初始下標從0開始（上述算法均是從1開始）//example:chars[100],t[100];cin>>s>>t;KMP(s,t);//獲取待查詢模式的next數組int*get_next(char*T,int*next){int i=0,j=-1;int length=strlen(T);int *temp=next; *next=-1; while(i<length) { if(j==-1||*(T+i)==*(T+j)) { i++; j++;//最佳化後的get_next方法，可以防止出現形如"aaaaab"這種模式的計算退化 if(*(T+i)!=*(T+j)) *(next+i)=j; else *(next+i)=*(next+j); } else j=*(next+j); } return temp;}//KMP算法intKMP(char*S,char*T){int S_Length=strlen(S);int T_Length=strlen(T);//若模式長度大於字元串，則直接返回查詢失敗if(S_Length<T_Length) return 0;int i=0,j=0;int *next=newint[T_Length]; get_next(T,next); while(i<S_Length&&j<T_Length) { if(j==-1||*(S+i)==*(T+j)) { i++; j++; } else j=*(next+j); } if(j>=T_Length) return i-T_Length; return 0;}在此提供一個更簡明的適用於字元串的kmp實現：
#include<iostream>#include<string.h>intnext[100];voidgetnext(charb[]){inti=1,j=0;//i是每個位子，j是回退的位子next[1]=0;while(i<=strlen(b)){if(j==0||b[i-1]==b[j-1]){i++;j++;next[i]=j;}elsej=next[j];//用上一個的回退關係}}intkmp(chara[],charb[]){inti=1,j=1;//i是主串中的位子，j匹配串的位子while(i<=strlen(a)&&j<=strlen(b)){if(j==0||a[i-1]==b[j-1]){i++;j++;}elsej=next[j];}if(j>strlen(b))returni-strlen(b);elsereturn0;}intmain(){chara[40],b[40];printf("要匹配的主串：\n");scanf("%s",a);printf("要匹配的目標字元串：\n");scanf("%s",b);getnext(b);printf("輸出next值：\n");for(inti=1;i<=strlen(b);i++)printf("%d",next[i]);printf("\n");printf("%d",kmp(a,b));system("pause");main();return0;}C示例改進過程
根據題設，程式可寫成：
voidGetNext(char*T,int*next){intk=1,j=0;next[1]=0;while(k<T[0]){if(j==0||T[k]==T[j]){++k;++j;next[k]=j;}elsej=next[j];}}但是這個不是最優的，因為他沒有考慮aaaaaaaaaaaaaaaaaaab的情況，這樣前面會出現大量的1，這樣的算法複雜度已經和最初的樸素算法沒有區別了。所以稍微改動一下：
voidGetNextEx(char*T,int*next){intk=1,j=0;next[1]=0;while(k<strlen(T)){if(j==0||T[k]==T[j]){++k;++j;if(T[k]==T[j])next[k]=next[j];elsenext[k]=j;}elsej=next[j];}}現在我們已經可以得到這個next字元串的值了，接下來就是KMP算法的本體了：
相當簡單：
intKMP(char*S,char*T,intpos){intk=pos,j=1;inttt=strlen(S);while(k<tt){if(S[k]==T[j]){++k;++j;}elsej=next[j];}if(j>T[0])returnk-T[0];elsereturn0;}和樸素算法相比，只是修改一句話而已，但是算法複雜度從O(m*n) 變成了：O(m+n)
對比
//findatemplateinastring.#include<string.h>#include<stdio.h>intIndex(char*S,char*T,intpos)//pos記錄從哪一位開始匹配可以直接用0代替{intk=pos,j=0;while(k<strlen(S)&&j<strlen(T))//未超出字元串的長度{if(S[k+j]==T[j])++j;//如果相同，則繼續向後比較else{k++;j=0;}//如果不同，就回溯，重新查找}if(j==strlen(T))returnk；elsereturn0;}實際套用
用KMP算法，計算串的最大匹配論文
摘要
給定兩個串S和T，長分別m和n，本文給出了一個找出二串間最大匹配的算法。該算法可用於比較兩個串S和T的相似程度，它與串的模式匹配有別。
關鍵字
模式匹配 串的最大匹配 算法
Algorithm on Maximal Matching of Strings
Lin YuCai Xiang YongHong Zhang ChunXia Zhang JianJun
（Computer Science Department of Yunnan Normal University Kunming 650092）
ABSTRACT Given Two Strings S of length m and T of length n，the paper presents an algorithm which finds the maximal matching of them. The algorithm can be used to compare the similarility of the two strings S and T,it is different with the strings' pattren matching.
KEY WORDS Pattern Matching Maximal Matching of Strings Algorithm
提出問題
字元串的模式匹配主要用於文本處理，例如文本編輯。文本數據的存儲（文本壓縮）和數據檢索系統。所謂字元串的模式匹配[2]，就是給定兩個字元串S和T，長度分別為m和n，找出T中出現的一個或多個或所有的S，在這方面已經取得了不少進展。本文從文本處理的另一個角度出發，找出兩個串的最大匹配，比較其相似程度。它主要套用於文本比較，特別是在計算機輔助教學中。顯然前者要找S的完全匹配，而後者並無此要求。例如，若S=ABCD，T=EFABCDX，那么模式匹配的結果就是找出了T中的一個ABCD，而我們算法的結果就是S能與T的ABCD完全匹配，但是T中還有3個字元是比S多出來的，也就是說在S中有100%的字元與T中的匹配，而在T中有57%的字元與S中的匹配。若S= ABCDFE，T=AFXBECDY。則在模式匹配中S與T無匹配項，但在我們的算法中就能發現T中存在A，B，C，D，但D後不存在E，F。而且S中也存在A，B，C，D，且具有順序性。這樣就能公正地評價S，T的區別。得知其相似程度。
文章的組織如下：首先介紹基本定義和問題的描述；第三節是算法設計；最後是本文總結。
問題描述
設∑為任意有限集，其元稱為字元，w：∑→N為∑到N的函式，稱為∑的權函式（註：本文僅討論權值恆為1的情況）。∑*為∑上的有限字元串集合，那么對任意S，T∈∑*，設S=a1a2…am，T=b1b2…bn，m>0，n>0。記<m>={1,2，…，m},<n>={1,2，…，n}，則稱{(i,j）∣i∈<m>；，j∈<n>；，ai=bj}為S與T的匹配關係集，記作M（S，T），稱M為S與T的一個（容許）匹配，若對任意（i,j），（i',j'）∈，① i< i'，若且唯若j< j'，② i= i'若且唯若j= j'。S與T的匹配中滿足 最大者，稱為S與T的最大匹配。若C(i,j）為N上的m×n矩陣，且滿足：
則稱矩陣C為串S與T的匹配關係陣。
於是求串S與T的最大匹配，等價於求C中的一個最大獨立點集M，它滿足，若ci,j，ci',j'∈M，則i< i' 若且唯若j< j'，i=i'若且唯若j=j'。我們稱這樣的最大獨立點集為C的最大C-獨立點集。
例：設∑為所有字母的集合，對任意x∈∑，w（x）≡1，設S與T分別為：S=“BOOKNEWS”，T=“NEWBOOKS”。則我們可以得到S與T兩個匹配：
這裡=5；
這裡 =4。
顯然為串S與T的最大匹配。
S與T的匹配關係陣C可表示如下：
其中帶圈的部分為一最大C-獨立點集。
設計
我們僅就權值為一的情況進行討論。
設S和T為任意給定串，C為的S與T匹配關係陣，那么由2的討論知，求S與T的最大匹配問題，等價於求C的最大C-獨立點集問題。因而，為了解決我們的問題，只要給出求C的最大C-獨立點集的算法就可以了。
顯然，為了求出C的最大C-獨立點集，我們可以採用這樣的方法：搜尋C的所有C-獨立點集，並找出它的最大者。這種方法是可行的，但並不是非常有效的。這會使問題變得很繁，複雜度很大。因此，我們先對問題進行分析。
在下面的討論中，我們把C的任一C-獨立點集={ai1,j1，…，ais,js}，記作=ai1,j1…ais,js，i1 <；…< is。於是可看作陣C中以1為節點的一條路，滿足：對路中的任意兩節點，均有某一節點位於另一節點的右下方。稱這種路為右下行路。
於是求C-獨立點集等價於求陣C的右下行路。這種求右下行路的搜尋可以逐行往下進行。
命題1. 若 =αai,jβ和ψ=α'ai,jσ為C的兩個C-獨立點集，且α為α'的加細，則存在C-獨立點集'=αai,jδ，滿足≥。
命題2. 若 =αai,jβ和ψ=α'ai+k,jσ為C的兩個C-獨立點集，且≥，則存在C-獨立點集'=αai,jδ，滿足≥。
命題3. 若 =αai,jβ和ψ=α'ai,j+kσ為C的兩個C-獨立點集，且≥，則存在C-獨立點集'=αai,jδ，滿足≥。
由命題1知，在搜尋右下行路的過程中，如果已獲得了某一C-獨立點集的某一初始截段αai,j和另一C-獨立點集ψ的某一初始截段α'ai,j，且有≤，則我們可以停止對ψ的進一步搜尋。
由命題2知，在搜尋右下行路的過程中，在某一列j存在某兩個C-獨立點集的某初始截段=ai1,j1…ais,j和ψ=al1,m1…alt,j，如果≥，但lt>is，則我們可以停止對ψ的進一步搜尋。
由命題3知，在搜尋右下行路的過程中，在某一行i存在某兩個C-獨立點集的某初始截段=ai1,j1…ai,js和ψ=ai1,m1…ai,mt，如果≥，但mt>js，則我們可以停止對ψ的進一步搜尋。
由此可見，並不要求搜尋所有C的最大C-獨立點集，而可以採用比這簡單得多的方法進行計算。那么按照我們上面的三個命題，來看如下實例：
首先我們得到=B（在上的節點用①表示），我們向右下方找路，可以發現，在第4列有兩個1，根據命題2，我們選擇上面的一個1，也就是說選擇第1行的那個1，而不要第2行的那個1。同時我們也發現在第1行也有兩個1，由命題3知，我們選擇左邊的那個1，即第4列的那個1。此時=BO。但是當我們的算法運行到第4行時，=BOOK，由於K在第3行第6列，而本行的1在第1列，在路最後一個節點K的左邊，那么我們必須新建一條路ψ，因為我們並不能確定是否以後就有≥，當算法運行到第6行時，=BOOK，ψ=NEW，=4，=3，我們將S鏈到路上，此時我們得到最長右下行路=BOOKS，=5。這樣我們就可以計算出這兩個字元串的匹配程度。
