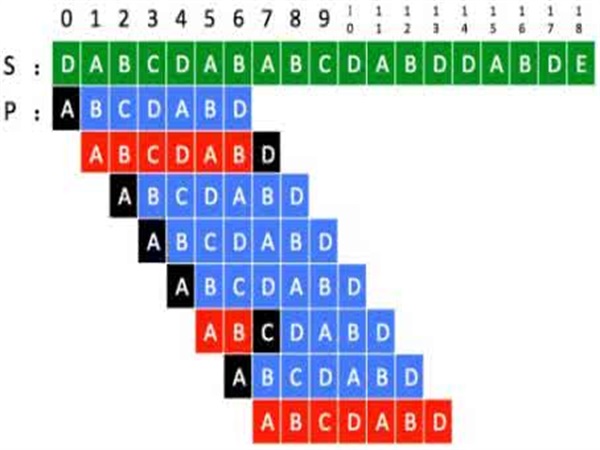
KMP算法是一種改進的字元串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同時發現,因此人們稱它為克努特-莫里斯-普拉特算法(簡稱KMP算法)。KMP算法的關鍵是利用匹配失敗後的信息,儘量減少模式串與主串的匹配次數以達到快速匹配的目的。因其操作方法簡單,又稱簡約KMP算法。
基本介紹
- 中文名:簡約KMP算法
- 外文名:Simple KMP algorithm
- 分類:計算機
- 定義:一種改進的字元串匹配算法
- 發現:克努特 莫里斯 普拉特
- 功能:快速匹配
- 方法:遍歷 匹配
簡介,思想,數組計算,字元串匹配,算法代碼,舉例,改進,
簡介
KMP算法是一種改進的字元串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同時發現,因此人們稱它為克努特-莫里斯-普拉特算法(簡稱KMP算法)。KMP算法的關鍵是利用匹配失敗後的信息,儘量減少模式串與主串的匹配次數以達到快速匹配的目的。因其操作方法簡單,又稱簡約KMP算法。
kmp算法完成的任務是:給定兩個字元串O和f,長度分別為n和m,判斷f是否在O中出現,如果出現則返回出現的位置。常規方法是遍歷a的每一個位置,然後從該位置開始和b進行匹配,但是這種方法的複雜度是O(nm)。kmp算法通過一個O(m)的預處理,使匹配的複雜度降為O(n+m)。
思想
我們首先用一個圖來描述kmp算法的思想。在字元串O中尋找f,當匹配到位置i 時兩個字元串不相等,這時我們需要將字元串f向前移動。常規方法是每次向前移動一位,但是它沒有考慮前i-1位已經比較過這個事實,所以效率不高。事實上,如果我們提前計算某些信息,就有可能一次前移多位。假設我們根據已經獲得的信息知道可以前移k位,我們分析移位前後的f 有什麼特點。我們可以得到如下的結論:
1、A段字元串是f的一個前綴;
2、B段字元串是f的一個後綴。
3、A段字元串和B段字元串相等。
所以前移k位之後,可以繼續比較位置i的前提是f的前 i-1個位置滿足:長度為i-k-1的前綴A和後綴B相同。只有這樣,我們才可以前移k位後從新的位置繼續比較。
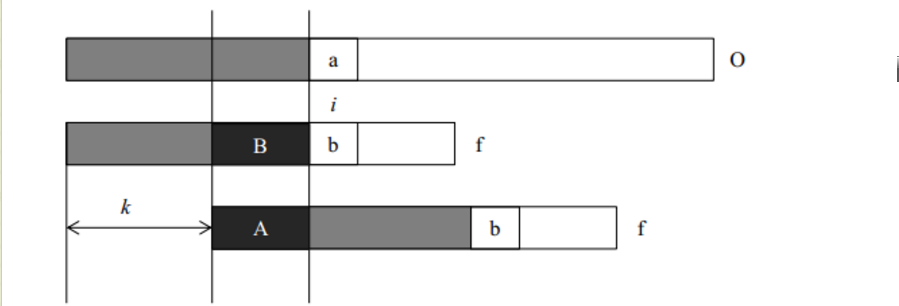
所以kmp算法的核心即是計算字元串f每一個位置之前的字元串的前綴和後綴公共部分的最大長度(不包括字元串本身,否則最大長度始終是字元串本身)。獲得f 每一個位置的最大公共長度之後,就可以利用該最大公共長度快速和字元串O比較。當每次比較到兩個字元串的字元不同時,我們就可以根據最大公共長度將字元串f 向前移動(已匹配長度-最大公共長度)位,接著繼續比較下一個位置。事實上,字元串f的前移只是概念上的前移,只要我們在比較的時候從最大公共長度之後比較f和O即可達到字元串f 前移的目的。

數組計算
理解了kmp算法的基本原理,下一步就是要獲得字元串f每一個位置的最大公共長度。這個最大公共長度在算法導論裡面被記為next數組。在這裡要注意一點,next數組表示的是長度,下標從1開始;但是在遍歷原字元串時,下標還是從0開始。假設我們現在已經求得next[1]、next[2]、……next[i],分別表示長度為1到i的字元串的前綴和後綴最大公共長度,現在要求next[i+1]。由上圖我們可以看到,如果位置i和位置next[i]處的兩個字元相同(下標從零開始),則next[i+1]等於next[i]加1。如果兩個位置的字元不相同,我們可以將長度為next[i]的字元串繼續分割,獲得其最大公共長度next[next[i]],然後再和位置i的字元比較。這是因為長度為next[i]前綴和後綴都可以分割成上部的構造,如果位置next[next[i]]和位置i的字元相同,則next[i+1]就等於next[next[i]]加1。如果不相等,就可以繼續分割長度為next[next[i]]的字元串,直到字元串長度為0為止。
字元串匹配
計算完成next數組之後,我們就可以利用next數組在字元串O中尋找字元串f的出現位置。匹配的代碼和求next數組的代碼非常相似,因為匹配的過程和求next數組的過程其實是一樣的。假設現在字元串f的前i個位置都和從某個位置開始的字元串O匹配,現在比較第i+1個位置。如果第i+1個位置相同,接著比較第i+2個位置;如果第i+1個位置不同,則出現不匹配,我們依舊要將長度為i的字元串分割,獲得其最大公共長度next[i],然後從next[i]繼續比較兩個字元串。這個過程和求next數組一致。
算法代碼
求next數組的代碼如下:
void get_next(string pattern, int next[]) {
int i = 0;
int j = 0; // j == -1
next[0] = -1; // next[0]
int p_len = pattern.length();
while (++i < p_len) {
if (pattern[i] == pattern[j]) {
next[i] = j++;
} else {
next[i] = j;
j = 0;
if (pattern[i] == pattern[j]) {
j++;}}
int j = 0;
next[0] = -1;
int p_len = pattern.length();
int matched = 0;
while (++j <= p_len) {
int right = j - 1;
int mid = floor(right / 2);
int left = right % 2 == 0 ? mid - 1 : mid;
int curLeft = left;
int curRight = right;
while (curLeft >= 0) {
if (pattern[curLeft] == pattern[curRight]) {
matched++;
curLeft--;
curRight--;} else {
matched = 0;
curLeft = --left;
curRight = right; } }
next[j] = matched;
matched = 0; }}}
根據next數組求模式串在主串中的位置代碼如下:
int search(string source, string pattern, int next[])
{
int i = 0;
int j = 0;
int p_len = pattern.length();
int s_len = source.length();
while (j < p_len && i < s_len)
{ if (j == -1 || source[i] == pattern[j])
{ i++;
j++; }
else { j = next[j];} }
if (j < pattern.length()) return -1;
else
return i - pattern.length();}
舉例
舉例來說,有一個字元串”BBC ABCDAB ABCDABCDABDE”,我想知道,裡面是否包含另一個字元串”ABCDABD”
首先,字元串”BBC ABCDAB ABCDABCDABDE”的第一個字元與搜尋詞”ABCDABD”的第一個字元,進行比較。因為B與A不匹配,所以搜尋詞後移一位。

因為B與A不匹配,搜尋詞再往後移。

就這樣,直到字元串有一個字元,與搜尋詞的第一個字元相同為止。

接著比較字元串和搜尋詞的下一個字元,還是相同。

直到字元串有一個字元,與搜尋詞對應的字元不相同為止。
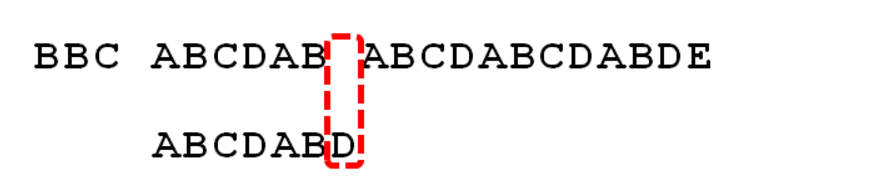
這時,最自然的反應是,將搜尋詞整個後移一位,再從頭逐個比較。這樣做雖然可行,但是效率很差,因為你要把”搜尋位置”移到已經比較過的位置,重比一遍。

一個基本事實是,當空格與D不匹配時,你其實知道前面六個字元是”ABCDAB”。KMP算法的想法是,設法利用這個已知信息,不要把”搜尋位置”移回已經比較過的位置,繼續把它向後移,這樣就提高了效率。

改進
KMP算法是串匹配算法中效率較高的,它充分利用模式信息,使得模式在跟主串匹配過程中主串的指針不回溯,從而具有較高的匹配速度,並在各種領域中有廣泛套用。然而,KMP算法仍存在著主串與模式多個相同字元重複比較的缺陷。在KMP算法的基礎上,提出一種改進的模式匹配算法,可以減少比較次數,提高匹配效率。
算法基本思想:引入模式串的Q(r)函式,在模式中就雙端分別求Q(r)函式值,根據模式兩端當前字元的Q(r)函式值,使模式交替向中間滑動儘可能遠的一段距離後,繼續匹配。