基本介紹
- 中文名:無理數
- 外文名:Irrational number
- 別稱:無限不循環小數
- 提出者:希伯索斯
- 套用學科:數學
- 性質:不能用分數進行表示
- 對應概念:有理數
- 所屬範圍:實數
定義,歷史,證明方法,拓展,實例,
定義
在數學中,無理數是所有不是有理數字的實數,後者是由整數的比率(或分數)構成的數字。當兩個線段的長度比是無理數時,線段也被描述為不可比較的,這意味著它們不能“測量”,即沒有長度(“度量”)。
常見的無理數有:圓周長與其直徑的比值,歐拉數e,黃金比例φ等等。
可以看出,無理數在位置數字系統中表示(例如,以十進制數字或任何其他自然基礎表示)不會終止,也不會重複,即不包含數字的子序列。例如,數字π的十進制表示從3.141592653589793開始,但沒有有限數字的數字可以精確地表示π,也不重複。必須終止或重複的有理數字的十進制擴展的證據不同於終止或重複的十進制擴展必須是有理數的證據,儘管基本而不冗長,但兩種證明都需要一些工作。數學家通常不會把“終止或重複”作為有理數概念的定義。
無理數也可以通過非終止的連續分數來處理。
無理數是指實數範圍內不能表示成兩個整數之比的數。簡單的說,無理數就是10進制下的無限不循環小數,如圓周率、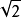 等。
等。
歷史
畢達哥拉斯(Pythagoras,約公元前580年至公元前500年間)是古希臘的大數學家。他證明許多重要的定理,包括後來以他的名字命名的畢達哥拉斯定理(勾股定理),即直角三角形兩直角邊為邊長的正方形的面積之和等於以斜邊為邊長的正方形的面積。畢達哥拉斯將數學知識運用得純熟之後,覺得不能只滿足於用來算題解題,於是他試著從數學領域擴大到哲學,用數的觀點去解釋一下世界。經過一番刻苦實踐,他提出“萬物皆為數”的觀點:數的元素就是萬物的元素,世界是由數組成的,世界上的一切沒有不可以用數來表示的,數本身就是世界的秩序。

不可約的本質是什麼?長期以來眾說紛紜,得不到正確的解釋,兩個不可通約的比值也一直認為是不可理喻的數。15世紀義大利著名畫家達.芬奇稱之為“無理的數”,17世紀德國天文學家克卜勒稱之為“不可名狀”的數。
然而真理畢竟是淹沒不了的,畢氏學派抹殺真理才是“無理”。人們為了紀念希伯索斯這位為真理而獻身的可敬學者,就把不可通約的量取名“無理數”——這就是無理數的由來。
由無理數引發的數學危機一直延續到19世紀下半葉。1872年,德國數學家戴德金從連續性的要求出發,用有理數的“分割”來定義無理數,並把實數理論建立在嚴格的科學基礎上,從而結束了無理數被認為“無理”的時代,也結束了持續2000多年的數學史上的第一次大危機。 分數=有限小數+無限循環小數,無限不循環小數是無理數
分數=有限小數+無限循環小數,無限不循環小數是無理數
 分數=有限小數+無限循環小數,無限不循環小數是無理數
分數=有限小數+無限循環小數,無限不循環小數是無理數證明方法
證明: √2是無理數
假設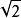 不是無理數
不是無理數
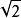
∴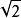 是有理數
是有理數
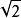
令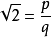 (
(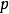 、
、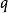 互質且
互質且 ,
,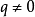 )
)
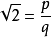
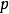
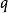

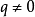
兩邊平方得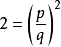
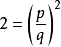
即

通過移項,得到: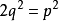
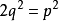
∵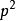 必為偶數
必為偶數
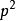
∴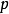 必為偶數
必為偶數
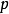
令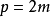
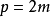
則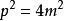
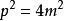
∴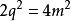
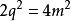
化簡得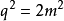
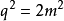
∵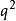 必為偶數
必為偶數
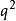
∴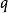 必為偶數
必為偶數
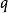
綜上,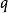 和
和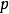 都是偶數
都是偶數
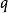
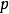
∵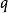 、
、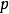 互質,且
互質,且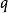 、
、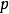 為偶數
為偶數
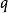
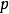
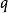
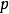
矛盾 原假設不成立
∴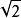 為無理數
為無理數
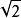
拓展
證明 是無理數(整數
是無理數(整數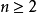 )
) ,
,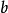 互素。
互素。

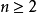

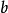
假設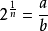 則存在
則存在
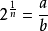
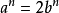
則a為偶數,設 ,
,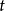 為正整數 代入上式有
為正整數 代入上式有

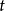

那么假設是不成立的
則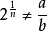
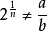
成立,那么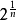 必為無理數。
必為無理數。
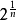
實例
如果正整數N不是完全平方數,那么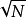 不是有理數(是無理數)。
不是有理數(是無理數)。
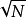
證明:若假設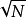 是有理數,不妨設
是有理數,不妨設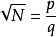 ,其中p與q都是正整數(不一定互質。若假定p、q互質則證法稍有變動)。
,其中p與q都是正整數(不一定互質。若假定p、q互質則證法稍有變動)。
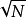
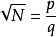
設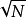 的整數部分為a,則有不等式
的整數部分為a,則有不等式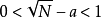 成立。兩邊乘以q,得
成立。兩邊乘以q,得
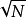
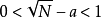

因p、q、a都是整數,p-aq也是一個正整數。
再在上述不等式的兩邊乘以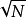 ,得
,得
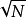
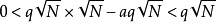
即:
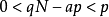
顯然,qN-ap也是一個正整數。
於是我們找到了兩個新的正整數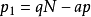 和
和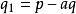 ,它們滿足
,它們滿足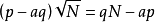 ,即
,即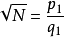 ,並且有
,並且有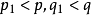 。
。
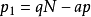
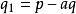
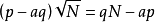
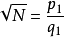
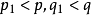
重複上述步驟,可以找到一系列的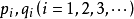 使得
使得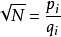 且
且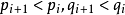 。因該步驟可以無限重複,意味著
。因該步驟可以無限重複,意味著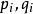 均可無限減小,但這與正整數最小為1矛盾。
均可無限減小,但這與正整數最小為1矛盾。
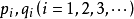
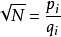
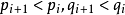
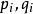
因此假設錯誤,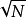 不是有理數。
不是有理數。