基本介紹
- 中文名:Warshall算法
- 提出者:Warshall
- 提出時間:1962年
- 性質:算法
算法思想
 算法
算法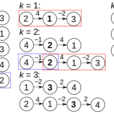
 算法
算法Warshall在1962年提出了一個求關係的傳遞閉包的有效算法。其具體過程如下,設在n個元素的有限集上關係R的關係矩陣為M:...
Floyd-Warshall算法是解決任意兩點間的最短路徑的一種算法。通常可以在任何圖中使用,包括有向圖、帶負權邊的圖。...
該算法也稱為Floyd算法,Roy-Warshall算法,Roy-Floyd算法或WFI算法。 [2] Floyd算法核心思路 編輯 Floyd算法路徑矩陣 通過一個圖的權值矩陣求出它的每兩點間的最...
Floyd-Warshall算法(Floyd-Warshall algorithm)是解決任意兩點間的最短路徑的一種算法,可以正確處理有向圖或負權的最短路徑問題。Floyd-Warshall算法的時間複雜度為O...
)是為解決最短路徑問題的算法,常見的有迪傑斯特拉算法(Dijkstra算法)(可進行堆最佳化),Bellman-Ford算法,SPFA算法(佇列最佳化的Bellma-Ford算法)和Floyd-Warshall算法。...
《算法設計與分析(第二版)》是西安電子科技大學出版社出版的一本圖書。作 者...7.3 Dijkstra算法 1757.4 Bellman Ford算法 1827.5 Floyd Warshall算法 184...
2.3.3 Dijkstra算法 2.3.4 Bellman-Ford-Moore算法 2.3.5 Floyd-Warshall算法 2.4 半徑、出半徑和直徑之間的不等式 2.4.1 強有向圖的半徑和直徑 ...
3、warshall算法:通過轉移矩陣的方式計算出可達矩陣4、疊代warshall算法對每個要素進行warshall操作後,記錄其狀態,下個要素疊代時候是以當前狀態為基礎進行疊代...
24.3 dijkstra算法24.4 差分約束與最短路徑24.5 最短路徑性質的證明第25章 每對頂點間的最短路徑25.1 最短路徑與矩陣乘法25.2 floyd-warshall算法...
在圖論中,可達性是指在圖中從一個頂點到另一個頂點的容易程度。在無向圖中,可以通過識別圖的連線分量來確定所有頂點對之間的可達性。 常用算法為:Floyd-Warshall...
warshell,沃舍爾算法的英文名。用來求有向圖的傳遞閉包。...... Warshall 算法(時間複雜度O(n^3))思想:動態規劃(記憶式)用動態規劃求關係的傳遞閉包...
Floyd算法\Floyd-Warshall算法Johnson算法A*算法所謂單源最短路徑問題是指:已知圖G=(V,E),我們希望找出從某給定的源結點S∈V到V中的每個結點的最短路徑。 [1...
Floyd-Warshall算法(英語:Floyd-Warshall algorithm),中文亦稱弗洛伊德算法,是解決任意兩點間的最短路徑的一種算法,可以正確處理有向圖或負權(但不可存在負權迴路)...
計算圖的傳遞閉包的有效算法可見於 here。最簡單的技術是Floyd-Warshall算法。 [3] 傳遞閉包Floyd-Warshall算法 單獨一條邊的路徑也不一定是最佳路徑。 從任意一條...
SPFA算法Bellman-Ford算法Floyd-Warshall算法Johnson算法V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近更新: 創建者:百科ROBOT...
