Q函式

標準常態分配的右尾函式，又叫（標準常態分配的）互補累計分布函式

基本介紹

• 中文名：Q函式
• 外文名：Q-function; Q function;
• 對比：誤差函式、互補誤差函式
• 性質：3條
• 別名：互補累計分布函式
• matlab函式：Q函式、Q反函式

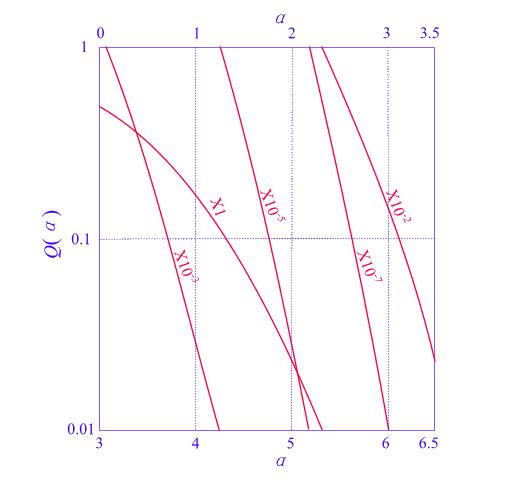
計算公式

其它函式關係

誤差函式

互補誤差函式

關係

性質

圖1 函式曲線

函式曲線示於圖1，圖1中各條曲線上的箭頭指向，是用來表示橫軸坐標的刻度在圖的上面還是下面。曲線上標註的乘因子用來與由該條曲線查得的縱軸坐標值相乘。例如，a=4.75，由下面的橫軸查得對應的縱軸值為0.103，曲線上的乘因子為10^-5，因此，Q（4.75）=0.103*10^-5=1.03*10^-4。

matlab函式

Matlab中本身有Q函式，即qfunc()

其反函式是

qfuncinv()

y = qfuncinv(x)

返回q函式的值為x的q函式的參數。輸入x必須是一個實數數組，包含0到1之間的元素。

下面的例子說明了qfunc和qfuncinv之間的反比關係。

x1 = [0 1 2; 3 4 5];

y1 = qfuncinv(qfunc(x1))

x2 = 0:.2:1;

y2 = qfunc(qfuncinv(x2))

輸出如下：

y1 = 0 1 2 3 4 5

y2 = 0 0.2000 0.4000 0.6000 0.8000 1.0000