定義
任何一個(n,k)分組碼,如果其信息元與監督元之間的關係是線性的,即能用一個線性方程來描述的,就稱為
線性分組碼。
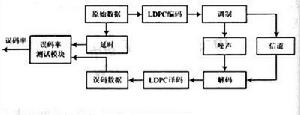
低密度奇偶校驗碼圖(LDPC碼)本質上是一種線形分組碼,它通過一個生成矩陣G將信息序列映射成傳送序列,也就是碼字序列。對於生成矩陣G,完全等效地存在一個奇偶校驗矩陣H,所有的碼字序列C構成了H的零空間 (null space),即
。
LDPC仿真系統圖LDPC 碼的奇偶校驗矩陣H是一個稀疏矩陣,相對於行與列的長度,校驗矩陣每行、列中非零元素的數目(我們習慣稱作行重、列重)非常小,這也是LDPC碼之所以稱為低密度碼的原因。由於校驗矩陣H的稀疏性以及構造時所使用的不同規則,使得不同LDPC碼的編碼二分圖(Taner圖)具有不同的閉合環路分布。而二分圖中閉合環路是影響LDPC碼性能的重要因素,它使得LDPC碼在類似可信度傳播(Belief ProPagation)算法的一類疊代解碼算法下,表現出完全不同的解碼性能。
LDPC碼
當H的行重和列重保持不變或儘可能的保持均勻時,我們稱這樣的LDPC碼為正則LDPC碼,反之如果列、行重變化差異較大時,稱為非正則的LDPC碼。研究結果表明正確設計的非正則LDPC碼的性能要優於正則LDPC。根據校驗矩陣H中的元素是屬於GF(2)還是GF(q)(q=2p),我們還可以將LDPC碼分為二元域或多元域的LDPC碼。研究表明多元域LDPC碼的性能要比二元域的好。
發展現狀
LDPC碼
LDPC碼
LDPC ( Low-density Parity-check,低密度奇偶校驗)碼是由 Gallager 在1963 年提出的一類具有稀疏校驗
矩陣的
線性分組碼 (linear block codes),然而在接下來的 30 年來由於計算能力的不足,它一直被人們忽視。1996年,D MacKay、M Neal 等人對它重新進行了研究,發現 LDPC 碼具有逼近香農極限的優異性能。並且具有解碼複雜度低、可並行解碼以及解碼錯誤的可檢測性等特點,從而成為了信道編碼理論新的研究熱點。
Mckay ,Luby 提出的非正則 LDPC 碼將 LDPC 碼的概念推廣。非正則LDPC碼 的性能不僅優於正則 LDPC 碼,甚至還優於 Turbo 碼的性能,是目前己知的最接近香農限的碼。
Richardson 和 Urbank 也為 LDPC 碼的發展做出了巨大的貢獻。首先,他們提出了一種新的編碼算法,在很大程度上減輕了隨機構造的 LDPC 碼在編碼上的巨大運算量需求和存儲量需求。其次,他們發明了密度演進理論,能夠有效的分析出一大類 LDPC 解碼算法的解碼門限。仿真結果表明,這是一個緊緻的解碼門限。最後,密度演進理論還可以用於指導非正則 LDPC碼 的設計,以獲得儘可能優秀的性能。
LDPC水印系統結構框圖LDPC碼具有巨大的套用潛力,將在深空通信、光纖通信、衛星數字視頻、數字水印、磁/光/全息存儲、移動和固定無線通信、電纜調製/解調器和
數字用戶線(DSL)中得到廣泛套用。
LDPC碼
M.Chiain 等對 LDPC 碼用於有記憶衰落信道時的性能進行了評估。B.Myher 提出一種速率自適應 LDPC 編碼調製的方案用於慢變化平坦衰落信道,經推廣還可用於 FEC-ARQ 系統。
Flarino 開發的集成了 V-DLPC 的 flash-OFDM 移動無線晶片組己可用於基於 IP 的移動寬頻網。VOCAL Technologies.Ltd 提出了一種用於 WLAN 的LDPC/Turbo 不對稱解決方案,即下行鏈路採用 LDPC 碼,上行鏈路採用 Turbo碼。研究表明採用該方案後用於IEEE802.11 a/b/gWLAN移動終端的電池壽命可延長至原來的4倍。
工業界也己經有 LDPC 編解碼晶片問世。其中,處於領先地位的 Flarion公司 推出的基於 ASIC 的 Vector-LDPC 解決方案使用了約 260 萬門,最高可以支持 50000的碼長,0.9 的碼率,最大疊代次數為 10,解碼器可以達到 10Gbps 的吞吐量,其性能己經非常接近香農限,可以滿足目前大多數通信業務的需求。AHA 公司、Digital Fountain公司也都推出了自己的編解碼解決方案。
優勢劣勢
和另一種近Shannon限的碼-Turbo碼相比較,LDPC碼主要有以下幾個優勢:
1. LDPC碼的解碼算法,是一種基於稀疏矩陣的並行疊代解碼算法,運算量要低於Turbo碼解碼算法,並且由於結構並行的特點,在硬體實現上比較容易。因此在
大容量通信套用中,LDPC碼更具有優勢。
2. LDPC碼的碼率可以任意構造,有更大的靈活性。而Turbo碼只能通過打孔來達到高碼率,這樣打孔圖案的選擇就需要十分慎重的考慮,否則會造成性能上較大的損失。
3. LDPC碼具有更低的錯誤平層,可以套用於有線通信、深空通信以及磁碟存儲工業等對誤碼率要求更加苛刻的場合。而Turbo碼的錯誤平層在10量級上,套用於類似場合中,一般需要和外碼級聯才能達到要求。
Turbo碼
4. LDPC碼是上個世紀六十年代發明的,現在,在理論和概念上不再有什麼秘密,因此在智慧財產權和專利上不再有麻煩。這一點給進入通信領域較晚的國家和公司,提供了一個很好的發展機會。
而LDPC碼的劣勢在於:
1. 硬體資源需求比較大。全並行的解碼結構對計算單元和存儲單元的需求都很大。
2. 編碼比較複雜,更好的編碼算法還有待研究。同時,由於需要在碼長比較長的情況才能充分體現性能上的優勢,所以編碼時延也比較大。
3. 相對而言出現比較晚,工業界支持還不夠。
圖表分析
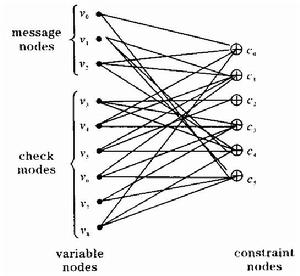
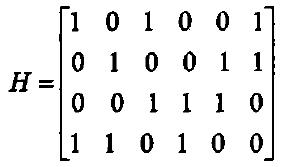
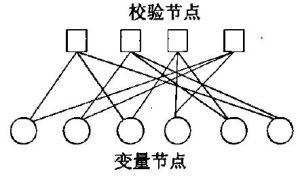
為了分析方便,我們一般用因子圖來表示一個LDPC碼。因子圖上所有的代碼點可以分成互不相關的兩類,我們稱之為信息點和校驗點。因子圖上的邊以一定的規律把它們連線起來,但是同一類中的代碼點不能用邊連線起來。事實上因子圖與用來定義碼字的奇偶校驗矩陣H是相對應的,即因子圖上的變數節點對應矩陣H的行向量,校驗節點對應因子圖上的列向量,而矩陣中非零元素就對應因子圖上的每一條邊。在定義新的碼字時,每一次構造的碼字在二進制矢量域中定義為x=(x1,x2,…,xn)。若且唯若方程Hx=0時為一碼字,也就是說,若且唯若每一個校驗點的相鄰變數節點的異或值為0時,對應的二進制矢量x=(x1,x2,…,xn)才是一個碼字。假設因子圖上每一個變數節點的度數是Y,每一個校驗點的度數是P,節點的次數為與該節點相聯邊的個數。如果Y,P相對於碼字總長n來說很小,則該因子圖對應的奇偶校驗矩陣是稀疏矩陣。
一個碼長n=6,碼率r=1/3,列重Y=2,行重P=3的校驗矩陣H和其對應的因子圖如下:
校驗矩陣 因子圖
LDPC碼
LDPC碼
校驗矩陣
因子圖
非正規與正規LDPC碼
在LDPC碼的校驗矩陣中,如果行列重量固定為(P,Y),即每個校驗節點有Y個變數節點參與校驗,每個變數節點參與P個校驗節點,我們稱之為正則LDPC碼。Gallager最初提出的Gallager碼就具有這種性質。從編碼二分圖的角度來看,這種LDPC碼的變數節點度數全部為P,而校驗節點的度數都為Y。我們還可以適當放寬上述正則LDPC碼的條件,行列重量的均值可以不是一個整數,但行列重量儘量服從均勻分布。另外為了保證LDPC碼的二分圖上不存在長度為4的圈。我們通常要求行與行以及列與列之間的交疊部分重量不超過1,所謂交疊部分即任意兩列或兩行的相同部分。我們可以將正則LDPC碼校驗矩陣H的特徵概括如下:
1. H的每行行重固定為P,每列列重固定為Y。
2. 任意兩行(列)之間同為1的列(行)數(稱為重疊數)不超過1,即H矩陣中不含四角為1 的小方陣,也即無4線循環。
3. 行重P和列重Y相對於H的行數M、列數N很小,H是個稀疏矩陣。
在正則LDPC碼的校驗矩陣中。行重和列重的均值保持不變,所以校驗矩陣中1的個數隨著碼長的增加而線性增長,整個校驗矩陣的元素個數則成平方增長。當碼長達到一定長度時,校驗矩陣H是非常稀疏的低密度矩陣。對於正則的LDPC碼,MacKay給出了以下兩個結論:
1. 對於任意給定列重大於3的LDPC碼,存在某個小於信道傳輸容量且大於零的速率r ,當碼長足夠長時,可以實現以小於r且不為零的速率無差錯的傳輸。也就是說任意給定一個不為零的傳輸速率r,存在一個小於相應香農限的噪聲門限,當信道噪聲低於該門限且碼長足夠長的時候,可以實現以r速率無差錯的傳輸。
2. 當LDPC碼的校驗矩陣H的列重Y不固定,而是根據信道特性和傳輸速率來確定時,則一定可以找到一個最佳碼,實現在任意小於信道傳輸容量的速率下無差錯的傳輸。
對於LDPC 碼的每個變數節點來說,當它參與的校驗式越多,即度數Y越大,則它可以從更多的校驗節點獲取信息,也就可以更加準確的判斷出它的正確值。對於H的每個校驗節點來說,當它涉及的變數節點越少,即度數P越小,則它可以更準確的估計相關變數節點的狀態。這種情況對於正則LDPc碼來說是一對不可克服的矛盾,於是Luby,Mitzemnacher等人就引入了非正則LDPC碼的概念。
在非正則LDPC碼的編碼二分圖中,兩個集合內部的節點度數不再保持相同,即每個變數節點參與的校驗式數目或每個校驗式中含有的變數節點數目不再保持均勻,而是有意設定部分突出的變數節點和校驗節點。在解碼過程中,那些參與較多校驗式的變數節點迅速得到它們的正確解碼信息,這樣它們就可以給相鄰的校驗節點更加有效的機率信息,而這些校驗節點又可以給與它們相鄰的次數少的變數節點更多的信息。整個解碼的過程呈現出一種波狀效應,次數越高的變數節點首先獲得正確信息,然後是次數較低的節點,然後依次往下,直到次數最低的變數節點。正是這種波狀效應,使得非正則LDPC碼獲得比正則LDPC更好的解碼性能。
二元域與多元域LDPC碼
對LDPC碼的定義都是在二元域基礎上的,MaKcay對上述二元域的LDPC碼又進行了推廣。如果定義中的域不限於二元域就可以得到多元域GF(q)上的LDPC碼。多元域上的LDPC碼具有較二進制LDPC碼更好的性能,而且實踐表明在越大的域上構造的LDPC碼,解碼性能就越好,比如在GF(16)上構造的正則碼性能己經和Turbo碼相差無幾。多元域LDPC碼之所以擁有如此優異的性能,是因為它有比二元域LDPC碼更重的列重,同時還有和二元域LDPC碼相似的二分圖結構。
假設在域GF(2)和域GF(q)(q=2p)上構造的LDCP碼所對應的校驗矩陣分別是H2和Hq。H2中的元素是0或1,而Hq是由元素0,1,…,q-1構成,Hq中的每個元素都是H2中p個元素的合成。如果設域GF(q)(q=2p)上的一個值a與一個1*p的二進制向量相關聯,那么把這個向量代入Hq中,就可以得到Hq的二進制表示。對於二進制LDPC碼來說,如果它的校驗矩陣H的列重量足夠大,那么它可以任意地接近香農限,但是如果增加列重量會使得二分圖中節點之間短圈的數H急劇增加從而使BP算法的性能下降。而在GF(q)域上構造的LDPC可以解決這個矛盾,它的檢驗矩陣H。可以增加與之對應的二進制校驗矩陣HZ中列的平均重量,且它的二分圖結構並沒有改變,不會造成節點之間短圈數目的增加,從而使得解碼性能得到顯著的提高。這種多元域上的編碼構造會增加解碼複雜度,但是相對於解碼性能的提高來說這種增加是值得的。
碼的構造
對LDPC碼來說,不考慮碼長和次數分布的情況下,校驗矩陣的結構就成了影響其性能的重要因素,反映在二分圖上對編碼性能有重要影響的就是圖中環的長度分布,需要採用一定的方法對校驗矩陣進行構造,獲得好的編碼。
目前LDPC碼的構造方法主要可以分為兩大類:隨機或偽隨機構造方法和代數的構造方法。
隨機或偽隨機的構造方法主要考慮的是碼的性能,在碼長比較長(接近或超過10000) 時,性能非常接近香農限。代數的構造方法通常考慮的是降低編解碼的複雜度,在碼長比較短的時候更有優勢。
1. Gallager LDPC碼
用和乘積算法(SPA:Sum-pordcuct algorithm)進行解碼取得最大後驗機率的解碼性能的條件是二分圖中沒有小的環,即girth為4的環,無4環的條件反映到二分圖中就是任意兩行中1的交迭數目不超過1個。無4環的二元高比特率LDPc碼可以通過隨機生成行構成,一般來說,這種方法不能生成固定行重量的矩陣。
Gallaegr提出了一種替代的方法:採用隨機置換的方法來構造規則LDPC碼。對於碼長為N的(j,k)正則碼,將M*N矩陣H通過j個大小為(M/j)*N的子矩陣構成,每個子矩陣本身也是LDPC矩陣,列重量為1,行重量為k,第一個子矩陣為階梯型,即第1行的k個1的列號是從(i-1)*k l到1*k,而其他子矩陣都是第一個子矩陣的隨機列置換,這樣每個子矩陣每行都有k個1,每列都有1個1。這種構造方法要求M必須是j的整數倍。
(20,3,4)LDPC碼的校驗矩陣
Gallager曾給出了一個碼長為20的規則(3,4)LDPC碼的校驗矩陣,如下所示。圖中的第一個子矩陣就是一個
階梯型矩陣,而第2個和第3個矩陣都是第一個子矩陣的列置換。

LDPC碼
Gallager同時證明了隨機置換得到的GaHager LDPC碼的最小漢明距離能夠隨著碼長的增加而線性增加,而且在對稱無記憶信道中,採用最大似然解碼時,其誤碼率隨著碼長的增加而呈指數形式下降,這說明隨機置換得到的Gallager LDPC碼是一類相當好的碼。
但是,Gallager在構造LDPC碼時採用的是隨機置換,這就給實現帶來了麻煩,就需要大量的存儲單元來存儲校驗矩陣中這些1的位置。
2. 確定性結構的LDPC碼
確定性結構的LDPC碼也稱為準循環LDPC碼。相對於隨機結構的矩陣是很容易獲得的確定性結構的矩陣,這種矩陣可以通過更少的參數來定義LDPC碼。確定性結構的LDPC碼的構造方法基於“陣列碼”(Array Code)。陣列碼是用來檢測和糾正突發差錯的二維碼。
通過三個參數定義LDPC碼。一個基本參數p和兩個整數j和k。令H為jp*kp的矩陣,定義為:
LDPC碼

LDPC碼
其中這裡的I是p*p的單位陣,Bi.j是Ip*p的左循環移位Bm.n或右循環移位Bm.n的置換矩陣。顯然,H矩陣中1的分布就只與循環位數Bm.n有關。對LDPC碼的分析就可以轉換為對Bm.n的分析。
將各小矩陣的循環移動位數寫成一個矩陣為
LDPC碼

LDPC碼
上面的校驗矩陣提供了一個可以用於SAP解碼的稀疏矩陣。而且,這個校驗矩陣結構上沒有四線循環。
解碼算法
LDPC碼編碼是在通信系統的傳送端進行的,在接收端進行相應的解碼,這樣才能實現編碼的糾錯。LDPC 碼由於其奇偶校驗矩陣的稀疏性,使其存在高效的解碼算法,其複雜度與碼長成線性關係,克服了分組碼在碼長很大時,所面臨的巨大解碼算法複雜度問題,使長碼分組的套用成為可能。而且由於校驗矩陣稀疏,使得在長碼時,相距很遠的信息比特參與統一校驗,這使得連續的突發差錯對解碼的影響不大,編碼本身就具有抗突發錯誤的特性。
LDPC碼的解碼算法種類很多,其中大部分可以被歸結到信息傳遞(Mesaseg Propagation,MP)算法集中。這一類解碼算法由於具有良好的性能和嚴格的數學結構,使得解碼性能的定量分析成為可能,因此特別受到關注。MP算法集中的置信傳播(BP)算法是Gallager提出的一種軟輸入疊代解碼算法,具有最好的性能。如果我們首先理解並掌握了一些很簡單的硬判決算法後,對BP算法的理解會更加容易。同時,通過一些常用的數學手段,我們可以對BP解碼算法作一些簡化,從而在一定的性能損失內獲得對運算量和存儲量需求的降低。
發展前景
LDPC碼具有很好的性能,解碼也十分方便。特別是在GF(q)域上的非規則碼,在非規則雙向圖中,當各變數節點與校驗節點的度數選擇合適時,其性能非常接近香農限。今後,LDPC碼的研究方向主要有:
(1)碼的設計;
(2)選擇合適的硬體(以降低編解碼的運算複雜性);
(3)LDPC碼套用於下一代通信系統。目前,LDPC碼已成為
第四代移動通信編碼技術中的首選。