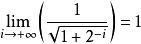CORDIC 理論,1.1、坐標旋轉數字計算機CORDIC,1.2、CORDIC原理,1.3、三角函式的計算,1.4、CORDIC的MATLAB 運算,現實意義,
CORDIC 理論
1.1、坐標旋轉數字計算機CORDIC 坐標旋轉數字計算機CORDIC(COordinate Rotation DIgital Computer)算法,通過移位和加減運算,能遞歸計算常用函式值,如Sin,Cos,Sinh,Cosh等函式,由J. Volder於1959年提出,首先用於導航系統,使得矢量的旋轉和定向運算不需要做查三角函式表、乘法、開方及反三角函式等複雜運算。J. Walther在1974年用它研究了一種能計算出多種超越函式的統一算法。
1.2、CORDIC原理 如圖所示,初始向量(X0,Y0)旋轉θ角度之後得到向量(X1,Y1),此向量有如下關係:X1=X0*cos(θ)-Y0*sin(θ)=cos(θ)(X0-Y0*tan(θ))
CORDIC算法 Y1=Y0*cos(θ)+X0*sin(θ)=cos(θ)(Y0+X0*tan(θ))
註:θ為待求角
假設初始向量經過N次旋轉之後得到新向量,且每次旋轉角度δ正切值都為2的冪,則第i次旋轉角度為δ=arctan(2^(-i)),即cosδ=(1/(1+2^(-2i)))^0.5。
容易得到角度θ≈∑S(i)●δ(i),其中S(i)=1或-1,表示旋轉角度的方向,
第i步旋轉可以表示為:
X(i+1)=((1/(1+2^(-2i)))^0.5)●(X(i)-S(i)Y(i)2^(-i))
Y(i+1)=((1/(1+2^(-2i)))^0.5)●(Y(i)+S(i)X(i)2^(-i))
其中(1/(1+2^(-2i)))^0.5)稱為校模因子 ,當旋轉次數一定時,趨於一個常數,Π(1/(1+2^(-2i)))^0.5)≈0.6073
X(i+1)=X(i)-S(i)Y(i)2^(-i)
Y(i+1)=Y(i)+S(i)X(i)2^(-i)
從而可以看出,對於移動的角度θ,現在只需要硬體加減法器和移位器就可以算出結果。引入Z,表示i次旋轉後相位累加的部分和,則:
Z(i+1)=Z(i)-S(i)arctan(2^(-i))
經過n次旋轉之後,Z→0,即與目標角重合,即:
X(n)=X1=X0*cos(θ)-Y0*sin(θ)
Y(n)=Y1=Y0*cos(θ)+X0*sin(θ)
1.3、三角函式的計算 以sin/cos計算為例,可利用正/餘弦的和角公式
遞歸 進行:
cos(a+b) = cos(a)cos(b) – sin(a)sin(b) = cos(a) [cos(b) – tan(a)sin(b)]
sin(a+b) = sin(a)cos(b) + cos(a)sin(b) = cos(a) [tan(a)cos(b) +sin(b)]
取a=arctan(2^-k), 即tan(a)=2^-k, 則cos(b) – tan(a)sin(b) 可通過移位和減法來實現。
如果角度z可以表示為z = s0 arctan(2^0) + s1 arctan(2^-1) + ... + sn arctan(2^-n), 其中s0, s1, ..., sn取+1或-1(+1可以理解為逆時針轉角,即加上一個角度; -1則相反) ,那么角度z的sin/cos計算可以通過一系列的移位和加減運算來實現。注意到cos(sk arctan(2^-k))=cos(arctan(2^-k)) 與轉角方向無關。此外,z應取第一項限角度(收斂域),對於其他項限角度,可由其第一項限對應角度變換得到。
相類似地,sinh/cosh的計算利用以下公式:
cosh(a+b) = cosh(a)cosh(b) + sinh(a)sinh(b) = cosh(a) [cosh(b) + tanh(a)sinh(b)]
sinh(a+b) = sinh(a)cosh(b) + cosh(a)sinh(b) = cosh(a) [tanh(a)cosh(b) + sinh(b)]
取a=arctanh(2^-k), 即tanh(a)=2^-k, 則cosh(b) + tanh(a)sinh(b) 可通過移位和減法來實現。如果參數z可以表示為z = s1 arctanh(2^-1) + s2 arctanh(2^-2) + ... + sn arctanh(2^-n), 其中s1, s2, ..., sn取+1或-1 ,那么z的sinh/cosh計算可以通過一系列的移位和加減運算來實現。
z應取[-ln2, ln2]範圍內的值,否則應先預處理 z = z’– pln2, 求得cosh(z’)/sinh(z’)的值,則
cosh(z) = cosh(z’)cosh(pln2) + sinh(z’)sinh(pln2) = ½[cosh(z’) + sinh(z’)]2^p + ½[cosh(z’) – sinh(z’)]2^-p
sinh(z) = sinh(z’)cosh(pln2) + cosh(z’)sinh(pln2) = ½[cosh(z’) + sinh(z’)]2^p + ½[sinh(z’) – cosh(z’)]2^-p 。
sin/cos和sinh/cosh的計算是CORDIC算法的兩個特例,CORDIC算法可描述如下:
給定初始值x(0), y(0), z(0),
x(k+1) = x(k) – ms(k)y(k)2^-q(m,k), y(k+1) = y(k) + s(k)x(k) 2^-q(m,k), z(k+1) = z(k) – s(k)d(k),
其中m表示模式,q(m,k) 為移位序列,s(k) 取+1或-1表示旋轉方向,d(k) 為遞進角度。
1.4、CORDIC的MATLAB 運算 以cos(a)/sin(a)計算為例,m = 1, x(0) = 1, y(0) = 0, z(0) = a, s(k) = sign(z(k)),移位序列q(1,k): 0, 1, 2, ..., 遞進角度為d(k)=arctan(2^-q(1,k)) 。
下面是實現的Matlab程式(保存為m檔案):
function [sin,cos] =cordic(angle);
% 初始化
x = 1;
y = 0;
z = angle;
a = 0;
d = 1;
k = 0.6073; %K 增益
x = k*x;
while a<100 %此處不能判斷d的符號控制循環,會死循環.套用a次數控制.
if z >=0
d=1;
else
d=-1;
end
xNew=x;
x=xNew-(y*d*(1/2^a));
y=y+(xNew*d*(1/2^a));
z=z-(d*(atan(1/2^a)));
a=a+1;
end
cos= x
sin= y
k值為cos(arctan(1)), cos(arctan(2^-1)), ..., cos(arctan(2^-K) 的連積值,收斂為0.6072529350。
以cosh(a)/sinh(a)計算為例,m = -1, x(0) = 1, y(0) = 0, z(0) = a, s(k) = sign(z(k)),移位序列q(-1,k): 1, 2, 3, 4, 4, 5, ... (3n+1重複兩次以保證收斂, 4, 13, 40, ...), 遞進角度為d(k)=arctanh(2^-q(-1,k)) 。
通過對初始值和旋轉方向s(k) 的選擇,模式m=0可以計算乘法和除法; 模式m=1可以計算sin/cos/arcsin/arccos/arctan; 模式m=-1可直接計算sinh/cosh/exp/arctanh/ln/sqrt, 間接計算arcsinh/arccosh,參見。
MATLAB 代碼實現2:
m=1;
u=1;
K=1.6468;
a=[0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ];
y0=0;
x0=1/K;
angle = 30;
z0=angle*pi/180;
for i=1:length(a)
x=x0-m*u*y0*2^(-a(i));
y=y0+u*x0*2^(-a(i));
z=z0-u*atan(2^(-a(i)));
x0=x;
y0=y;
z0=z;
u=sign(z0);
end
cosine = x;
sine = y;
MATLAB 代碼實現3:
function [cordic_x,cordic_y,cordic_z]=cordic(x,y,z,m,rotation,iterate)
%% [cordic_x,cordic_y,cordic_z]=cordic(x,y,z,m,rotation,iterate)
%% iterate: iterate times
%% rotation: set to 1 with rotation mode; otherwise set to 0 with vector mode.
%% cordic Algorithm for rotation:Z->0
%% m = 1 :(x,y,z)=(1,0,z); x = cos(z) ;y =sin(z)
%% m = 0 :(x,y,z)=(x,0,z);y = x*z
%% m = -1 :(x,y,z)=(1,0,z); x = cosh(z) ; y = sinh(z) ;
%% exp(z) = cosh(z) + sinh(z)
%%-------------------------------------------------------------------------
%% cordic Algorithm for Vector:y->0
%% m = 1 :(x,y,z)=(x,y,0); z = atan(y/x) ; x = (x^2+y^2)^(1/2)/scale
%% m = 0 :(x,y,z)=(x,y,0); z = y/z
%% m = -1 : (y<x),(x,y,z)=(x,y,0); z =atanh(y/x) ; x = (x^2-y^2)^(1/2)/scale
if(m==-1) %% hyperbolic
k_initial = 1; %% in hyperbolic mode , the k's initial value should be "1"
scale = 1.2075 ;
elseif(m==1) %% circyle
k_initial = 0;
scale = 0.6073;
else %% line
k_initial = 0;
scale = 1;
end
x=x*scale;
for k = k_initial : iterate
if(m==-1)&&(mod(k,3)==1)&&( k~=1) %% in hyperbolic mode ,should iterate twice while k == 3N+1
for i = 1:2
if(m == 1)
u=atan(2^(-k))*180/pi;
elseif(m == 0)
u=2^(-k);
elseif(m == -1)
u=atanh(2^(-k));
end
xpre=x;
ypre=y;
zpre=z;
upre=u;
if(rotation) d = sign(zpre);
else d = -sign(ypre);
end
x=xpre-m*d*ypre*2^(-k);
y=ypre+d*xpre*2^(-k);
z=zpre-d*upre;
end
else
if(m == 1)
u=atan(2^(-k))*180/pi;
elseif(m == 0)
u=2^(-k);
elseif(m == -1)
u=atanh(2^(-k));
end
xpre=x;
ypre=y;
zpre=z;
upre=u;
if(rotation) d = sign(zpre);
else d = -sign(ypre);
end
x=xpre-m*d*ypre*2^(-k);
y=ypre+d*xpre*2^(-k);
z=zpre-d*upre;
end
end
cordic_x=x;
cordic_y=y;
cordic_z=z;
現實意義 由於具有頻率精度高、轉換時間短、頻譜純度高以及頻率相位易編程等特點,數控振盪器(NCO)被廣泛套用於軟體
無線電 數字上、下變頻以及各種頻率和相位數字
調製解調 系統中。NCO傳統的實現方法主要有查表法、多項式展開法或近似法,但這些方法在速度、精度、資源方面難以兼顧。而採用CORDIC算法來實現超函式時,則無需使用乘法器,它只需要一個最小的
查找表 (LUT),利用簡單的移位和相加運算,即可產生高精度的正餘弦波形,尤其適合於FPGA的實現。
數字控制 振盪器(NCO,numerical controlled oscillator)是軟體無線電、直接數據頻率合成器(DDS,Direct digital synthesizer)、快速傅立葉變換(FFT,Fast Fourier Transform)等的重要組成部分,同時也是決定其性能的主要因素之一,隨著晶片集成度的提高、在
信號處理 、數字通信領域、
調製解調 、變頻調速、制導控制、電力電子等方面得到越來越廣泛的套用。
 CORDIC算法
CORDIC算法