Decimation Filter

軟體無線電的設計思想之一是將A/D 轉換器儘可能靠近天線，即把A/D從基帶移到中頻甚至射頻，把接收到的模擬信號儘早數位化。由於數位訊號處理器（DSP）的處理速度有限，往往難以對 A/D採樣得到的高速率數位訊號直接進行各種類別的實時處理。為了解決這一矛盾，需要採用數字下變頻（DDC）技術，將採樣得到的高速率信號變成低速率基帶信號，以便進行下一步的信號處理。

基本介紹

• 中文名：抽取濾波器
• 外文名：Decimation Filter
• 原理：轉變頻率
• 設計思想：將A/D 轉換器儘可能靠近天線

引言

數字下變頻技術在軟體無線電和各類數位化接收機中得到了廣泛套用。因此建立軟體無線電的通用數字下變頻器是非常必要的。

下變頻器的結構與組成

我們要設計數字下變頻器如圖1所示。

量化的中頻數位訊號進入數字下變頻器後，先與數字控制振盪器產生的本地數字載波混頻，經過CIC抽取濾波器，HBF抽取濾波器，FIR低通濾波對信號進行D倍抽取後得到正交基帶信號，這是下變頻過程。虛線框內為數字下變頻部分是我們設計和討論的重點。

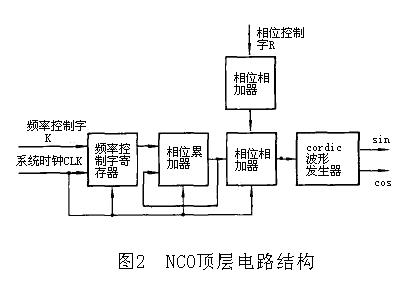
數字控制振盪器振盪器

如圖1所示。正交數字下變頻器前端包括兩部分一是乘法器；一是NCO。乘法器設計很簡單，NCO的目標是產生一個理想的正弦和餘弦波。更確切地說是產生一個可變頻率的正弦波樣本如公式：其中為本地振盪頻率； 為DDC輸入信號的採樣頻率。正弦波樣木可以用實時計算的方法產生，但這隻適用信號採樣頻率很低的情況。在軟體無線電高速信號採樣頻率的情況下，NCO實時計算的方法是不可取的。NCO產生正弦波樣本通常採用查表法，通過輸入的相位數據來定址查表輸出相應的正弦波幅值。對於一個相位位數為n，輸出信號幅度位數為M的數控振盪器，這就需要耗費大量的ROM資源(2nX Mbit)。為了避免使用大容量的存儲器。可採用了一種基於CORDIC( Coordinate Rotation Digital Computer)算法來產生正/餘弦樣本。該算法有線性的收斂域和序列特性。只要疊代次數足夠，即可保證結果有足夠的精度。並且用於混頻的乘法器也可以省掉。從而還節省了大量的邏輯硬體資源。使得數字下變頻更易於用FPGA來實現。

3.1、CORDIC算法

CORDIC算法基本原理是：設初始向量x0+jy0經旋轉角度後得到的向量 xn+jyn即， ，設旋轉基本角度θi，令 ，那么初始向量可通過一系列的基本角度θi的旋轉，逐漸逼近目標向量。在旋轉模式下，如果設Z0=θ ，根據J，S，WALTER的推導有：

（1）

其中

δi代表向量旋轉方向

經過n 次旋轉疊代後的結果為：

其中，，稱為模校正因子。如果令 ， y0=0，則，由上述推導可知：若已知角度Z0 和初始向量的 x0，y0 可由式(1)疊代運算得到角度Z0的正餘弦值，而式(3)中的疊代運算用硬體實現時非常方便，只有加（減）和移位操作。

3.2、基於CORDIC算法實現NCO

我們設計的NCO頂層結構為圖2所示。我們可以看到，頻率控制字暫存器將接收到的頻率控制字K送入相位累加器，累加器對系統時鐘進行累加計數，當到達輸入頻率控制字的值時對相位進行累加，隨後將累加值送入相位相加器，與相位控制字暫存器接收到的初始相位相加，得到當前的相位值。經過上述相位處理之後，即可獲得相位的正/餘弦相位序列，將此序列送入基於CORDIC算法的波形發生器，最終獲得兩路正交的正/餘弦輸出序列。

採用了流水線型實現結構，它用n級相似的算法單元在同一個時鐘周期內並行工作，每級算法單元的具體實現結構如圖3所示。圖中的三個累加器分別完成了該級中xi，yi，zi的疊代，累加器的加/減控制信號為上一級算法單元中的di信號，兩個i位的右移暫存器(註：圖中的>>i表示右移i位)完成了疊代等式中的乘2-i運算，而該級的基本旋轉角度值(2-i)可以採用直接硬連線。

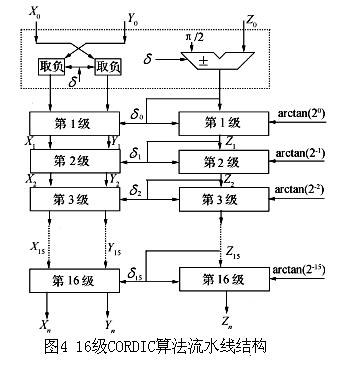
流水線結構的最大優點在於它的運算速度很快在任何一個時鐘周期，n級算法單元都同時工作，如在輸入端連續不斷地送入數據，那么在n個時鐘周期的延遲之後，輸出端將連續得到相應的下變頻後的數據與傳統的串列結構相比，流水線結構的運算速提高了n倍。圖4給出了16級流水線算法

的實現結構虛線框中部分是個初始化旋轉單元，是因為。由此可見，當疊代的次數n趨近於無窮大時，所被 覆蓋的角度只能是在-99.9度~99.9度之間，若想讓的覆蓋範圍擴展到，必須在疊代之前再增加一個初始化旋轉，將輸入向量先旋轉 ，之後是16級流水線算法單元，最右邊的是級的基本旋轉角度值(2-i)，di為各級累加器加/減控制信號"X0，Y0，Z0為下變頻模組的數據輸連線埠，Xn，Yn，Zn是三個輸出連線埠"。

3.3、初始化旋轉單元代碼

輸入為x_in y_in z_in 輸出為 phi，eps，r 定義信號為x，y，z

---Test for x_in<0 rotate 0，+90，or -90 degrees

IF x_in>o THEN

x <=x_in

y<=y_in

z<=z_in

ELSEIF y_in>0 THEN

x<=y_in

y<=-x_in

z<=z_in+90

ELSE

x<=-y_in

y<=x_in

z<=z_in-90

END IF

積分梳狀(CIC)濾波器的FPGA設計

CIC濾波器由兩部分組成，積分器和梳狀濾波器的級聯其衝擊回響為

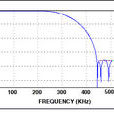
圖5顯示的是它的頻譜圖。CIC所有係數都為1，實現起來極其簡單，它不需要任何乘法運算，不需要存儲濾波器係數。為了加大阻帶衰減，通常採用N級CIC濾波器如圖6所示。

半帶抽取濾波器(HBF)的FPGA設計

HBF濾波器特別適合於實現2的冪次方倍的抽取，且計算效率高、實時性強。其頻譜如圖7所示。半帶濾波器是頻率回響滿足阻頻寬度與通頻寬度相等，當抽取率為2的冪次方時實現如圖8所示。