基本介紹
- 中文名:Burgers方程
- 外文名:Burgers equation
- 領域:數理科學
- 性質:非線性偏微分方程
- 作用:模擬衝擊波的傳播和反射
- 相關名詞:偏微分方程
簡介
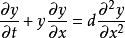
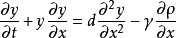
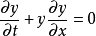
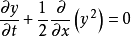
求解
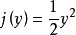
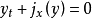


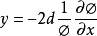
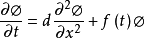
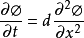
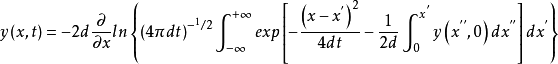
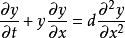
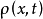
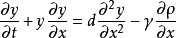
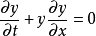
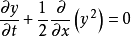
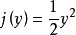
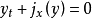


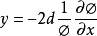
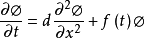
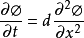
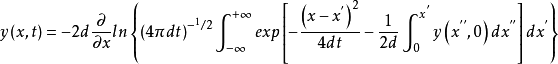
伯格斯方程(Burgers equation) 是一個模擬衝擊波的傳播和反射的非線性偏微分方程。伯格斯方程是套用數學的各個領域的基本偏微分方程,如流體力學,非線性聲學,氣體動力...
KdV-Burgers也稱Burgers-KdV方程是一個非線性偏微分方程.人們在研究含氣泡的液體流動以及彈性管道中的液體流動問題時,相繼提出了KdV-burgers方程,也有人將它用於湍流...
非線性偏微分方程的在物理學、氣動力學、流體力學、大氣物理、海洋物理、爆炸...KdV-Burgers KdV-Burgers方程 Modified KdV-Burgers 變形KdV-Burgers方程 Fifth...
3.3非線性偏微分方程的並行MOL方法 3.3.1Burgers方程的初邊值問題求解 3.3.2數值模擬 3.4本章小結 參考文獻 第4章二維偏微分方程的數值算法及套用 ...
8.7Burgers方程168 第9章吸收邊界條件與其他人工邊界條件172 9.1擬微分運算元172 9.2吸收邊界條件173 9.3一些近似式175 9.4Bayliss—Turkel輻射邊界條件179 ...
Burgers方程組的強Feller性奇異核的Dunkl變換向量值熱方程的全局估計熱流形變及不定號橢圓方程一個房屋市場價格系統的可控可觀性分析...
4.4 Levy過程驅動的非Lipschitz係數的隨機發展方程4.5 Levy過程驅動的隨機Burgers方程的動力學4.6 Levy時空白噪聲驅動的分數階偏微分方程...
4.在1996年首先提出了利用混合元方法對RLW方程、Burgers方程以及非飽和水流方程等非線性發展方程進行理論研究和數值模擬,這些結果已經在SIAM J.Numer. Anlysis和國內...
7. 廣義變係數Burgers方程的顯示精確解,《河南大學學報》2011;8. 兩類變係數KDV方程的顯示精確解,《河南師範大學學報》2011;9. AN EXTENDED (G/G)-EXPANSION ...
11.1Burgers方程與KdV方程 11.2Rossby孤立波 11.3Rossby包絡孤立波 11.4Rossby偶極子(modon) 11.5Rossby代數孤立波 11.6強迫Rossby孤立波 思考題 ...
第七節 Burgers方程的解析解 第八節 KdV方程之解的性質與相似規律第七章 孤立波的典型方程解 第一節 非線性效應 第二節 擴散波 第三節 KdV方程的孤立波解 ...
14.2Burgers方程與衝擊波第三篇積分變換第15章傅立葉變換15.1傅立葉變換的定義及其基本性質15.2用傅立葉變換解數理方程舉例習題15...
