KdV-Burgers方程

KdV-Burgers也稱Burgers-KdV方程是一個非線性偏微分方程.

人們在研究含氣泡的液體流動以及彈性管道中的液體流動問題時，相繼提出了KdV-burgers方程，也有人將它用於湍流的研究中，其形式為：

u_t+u*u_x-α*u_xx-β*u_xxx=0

其中參數α、β分別表示耗散和色散係數，這個方程可看作是最簡單的耗散方程。（李志斌《非線性數學物理方程的行波解》）

非線性偏微分方程

KdV-Burgers也稱Burgers-KdV方程是一個非線性偏微分方程：

行波解

KdV-Burgers方程有三角函式、雙曲函式行波解：

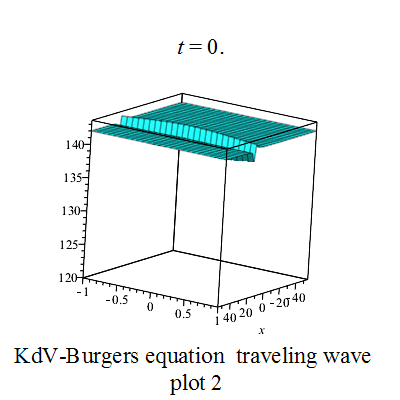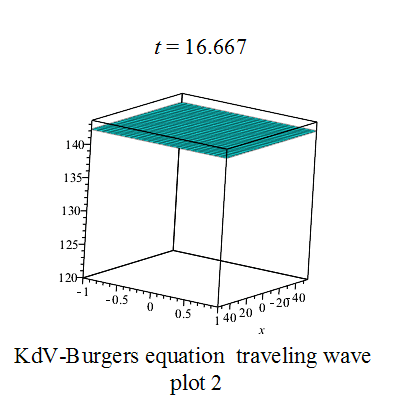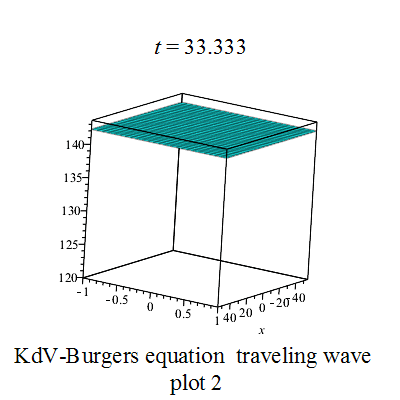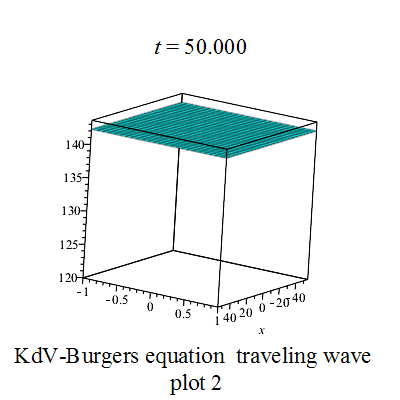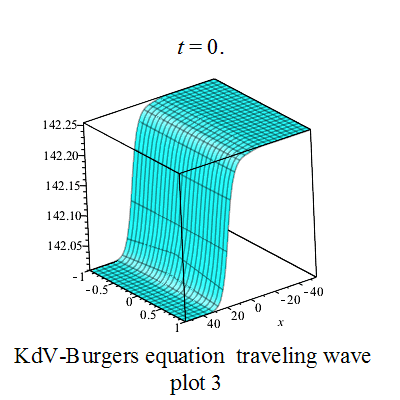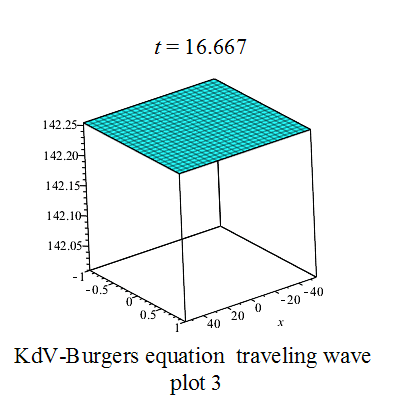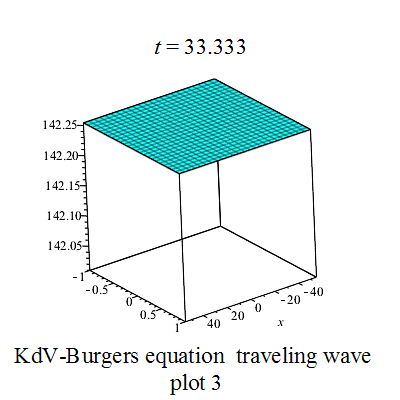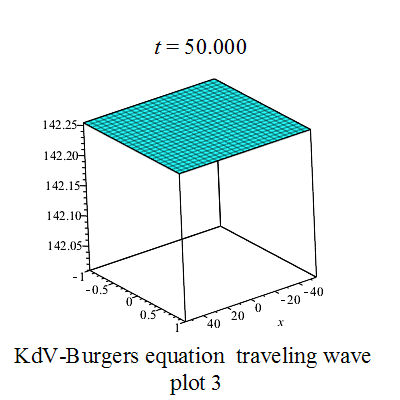行波圖

行波圖