基本介紹
定理內容






物理套用
矢量分析



靜電學







磁場

靜電場與磁場
數學中
高斯定理2


高斯公式一般指本詞條




















高斯公式用散度表示為:其中Σ是空間閉區域Ω的邊界曲面,而 是曲面Σ上的朝外的單位法向量。用向量表示 令V代表有一間單閉曲面S為邊界的體積,是定義在V中和S上連續可微的向量場。如果 是外法向向量面元,則 推論 對於標量函式g和向量場F的積,套用高斯公式可得:對於兩個向量場 的向量積,套用高斯公式可得:...
Gauss–Bonnet theorem)成立於偶數維數的閉黎曼流形。在偶數維數的閉黎曼流形,歐拉示性數仍然可以表達為曲率多項式的積分。公式:這是對於高維空間的直接推廣。例如在四維空間:二維高斯-博內定理的操作式證明 陳省身大師曾給出高維里高斯-博內定理的一個內蘊證明。用指南車也能給出二維高斯-博內定理的操作式證明。
成像公式,即透鏡成像公式、高斯成像公式,其形式為1/f=1/u+1/v。其中f為焦距,凸正凹負;u為物距;v為像距,實正虛負。推導方法 凸透鏡的成像規律是1/u+1/v=1/f(即:物距的倒數與像距的倒數之和等於焦距的倒數。)一共有兩種推導方法 。分別為“幾何法”與“函式法”幾何法 【題】如圖1 ,用幾何...
等差數列求和公式:Sn=(a1+an)n/2 Sn=n(2a1+(n-1)d)/2 Sn=An2+Bn d=公差 A=d/2 B=a1-(d/2)人物介紹 約翰·卡爾·弗里德里希·高斯(Johann Carl Friedrich Gauss ,1777年4月30日-1855年2月23日)德國著名數學家、物理學家、天文學家、大地測量學家,是近代數學奠基者之一,被認為是歷史上最...
高斯—波涅公式(Gauss–Bonnet formula)也叫高斯—波涅定理(Gauss–Bonnet theorem),是微分幾何中的重要定理,它描述了內角和與高斯曲率間的關係。公式如下:推廣 陳省身推廣了高斯—波涅公式,發現了陳—高斯—波涅定理(Chern–Gauss–Bonnettheorem)。Atiyah和Singer最終又將陳—高斯—波涅定理髮展為阿蒂亞-辛格...
用高斯公式推導普通物理中的高斯定理,設S內有一點電荷Q其電場過面積元dS的通量為 E·dS=Ecosθds =Q/(4πε0r^2)* cosθds θ為(ds^r) ε0---真空中的介電常數 顯然cosθds為面元投影到以r為半徑的球面的面積,在球體內,面元dS對電荷Q所張的立體角為dΩ= cosθds/r^2 故 E·ds= Q/(...
高斯一拉蓋爾求積公式 高斯一拉蓋爾求積公式(Gauss-Laguerre quadra-)一種高斯型求積公式.指積分區間為[0,權函式
高斯擴散模型適用於均一的大氣條件,以及地面開闊平坦的地區,點源的擴散模式。排放大量污染物的煙囪、放散管、通風口等,雖然其大小不一,但是只要不是討論煙囪底部很近距離的污染問題,均可視其為點源。計算公式 在下風向任意點(X,y,Z)的污染物濃度公式如圖1:坐標系 高斯模式的坐標系如圖2所示,其原點為...
高斯混合模型就是用高斯機率密度函式(常態分配曲線)精確地量化事物,它是一個將事物分解為若干的基於高斯機率密度函式(常態分配曲線)形成的模型。定義 高斯模型就是用高斯機率密度函式(常態分配曲線)精確地量化事物,將一個事物分解為若干的基於高斯機率密度函式(常態分配曲線)形成的模型。 對圖像背景建立高斯...
在數學中,陳定理(或陳–高斯–博內定理)是:2n維黎曼流形的歐拉示性數可以從曲率計算出來。陳定理也是高斯-博內定理(n=1)的推廣,在數學和理論物理學中亦有許多套用。此定理是以陳省身、高斯、與博內命名的。它由陳省身大師於1945年證出。陳定理將全局拓撲學與局部幾何連線起來。公式 若M是2n維的黎曼流形...
高斯函式以大數學家約翰·卡爾·弗里德里希·高斯的名字命名。高斯函式套用範圍很廣,在自然科學、社會科學、數學以及工程學等領域都能看到它的身影。定義 高斯函式的形式為:其中a、b與c為實數常數,且a> 0。c= 2的高斯函式是傅立葉變換的特徵函式。這就意味著高斯函式的傅立葉變換不僅僅是另一個高斯函式,而且...
表述地磁場的一種數學理論。1839年,C.F.高斯把球諧函式分析方法套用於地磁場,得出了地磁場的數學表達形式,奠定了地磁學的數理基礎。信息介紹 按照高斯理論,磁勢W應滿足拉普拉斯方程,它的解為:由地磁場的北向強度和東向強度可得到類似的公式。因此,如已知Z和X、Y的地面分布的實測值,就可按上述公式求出各階...
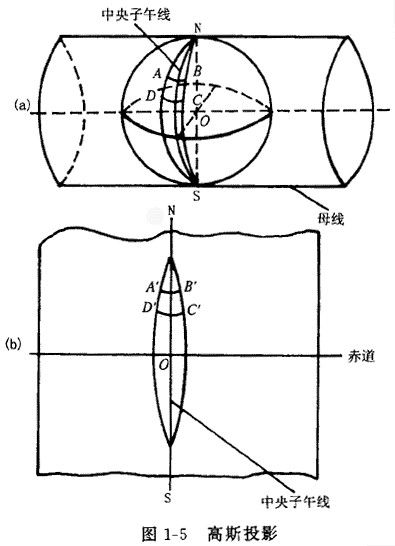
為了方便工程的規劃、設計與施工,我們需要把測區投影到平面上來,使測量計算和繪圖更加方便。而地理坐標是球面坐標,當測區範圍較大時,要建平面坐標系就不能忽略地球曲率的影響。把地球上的點位化算到平面上,稱為地圖投影。地圖投影的方法有很多,我國採用的是高斯——克呂格投影(又稱高斯正形投影),簡稱高斯...
我國各種大、中比例尺地形圖採用了不同的高斯-克呂格投影帶。其中大於1:1萬的地形圖採用3°帶;1:2.5萬至1:50萬的地形圖採用6°帶。投影與變形 地圖投影:就是將橢球面各元素(包括坐標、方向和長度)按一定的數學法則投影到平面上。研究這個問題的專門學科叫地圖投影學。可用下面兩個方程式(坐標投影公式)...
高斯公式 高斯公式的物像位置是相對於理想光學系統的主點來確定的。如圖5所示,以 表示物點A到物方主點H的距離,以 表示像點A′到像方主點H′的距離。方向規定以主點為原點,如果由H到A或由H′到A′的方向與光線的傳播方向一致,則為正;反之為負。由圖5可得 代入牛頓公式整理得 兩邊同時除以 ,有 這就是...
函式y=[x]稱為取整函式,也稱高斯函式。其中不超過實數x的最大整數稱為x的整數部分,記作[x]。該函式被廣泛套用於數論,函式繪圖和計算機領域。定義 記對應法則 為 顯然,是定義在全體實數集 的函式,而函式值是離散的。這個函式即為取整函式。為了方便,用 表示不超過 的最大整數,所以函式 又可記為 一般...
。顯然,高斯和勒讓德提出的漸進公式是等階的,實際上都等同於猜想 (不過高斯更深刻和精確),即素數定理。之後,俄國數學家切比雪夫(即帕夫努季·利沃維奇·切比雪夫,ПaфHутий Лbвович Чебышев)證明: 存在兩個正常數C₁和C₂,使不等式 對充分大的x成立,並且相當精確地定...
。該式描述為空間中某一點的電位移矢量的散度等於該處的電荷密度。微分形式的庫侖定理也被稱為電場的高斯定律,是麥克斯韋方程組的一部分。適用範圍 適用條件 在庫侖定律的常見表述中,通常會有真空和靜止,是因為庫侖定律的實驗基礎—扭秤實驗,為了排除其他因素的影響,是在亞真空中做的。另外,一般講靜電現象時,...
1)將所有的高斯核按照 ω / σ 降序排序 2)選擇滿足公式的前M個高斯核:M = arg min(ω / σ > T)3)如果當前像素點的像素值在中有一個滿足:就可以認為其為背景點。4、 更新背景圖像,用線上EM算法。EM算法 EM (Expectation Maximization)算法是由Dempster、Laind和Rubin在1977年提出的一種求參數的極...
,xₘ取為區間[α,b]上關於權函式ω(x)的m+1次正交多項式的零點,內插型求積公式即達到最高代數精度2m+1。這裡[α,b] 可以是有限或無限區間,ω(x)為取正值的權函式。許多有關數值積分的論著都列舉出各種高斯型公式的結點和係數的數值。可以證明:對每個連續函式,當結點個數趨於無窮時,高斯型公式所給出...
古典幾何的另一個重要發現就是高斯-博納特公式,它反映了曲率和彎曲空間裡的三角形三角之和的關係。 研究內蘊幾何的學科首屬黎曼幾何·黎曼在一次著名的演講中,創立了這門奠基性的理論。它首次強調了內蘊的思想,並將所有此前的幾何學對象都歸納到更一般的範疇里,內蘊地定義了諸如度量等等的幾何概念。這門幾何理論...
正弦積分是由積分定義的一種特殊函式。英文翻譯為sine integral,常用於計算正弦積分函式值,在性質上常與餘弦積分作比較。定義 正弦積分函式的定義為:,本函式採用勒讓德-高斯求積公式計算該積分。正弦積分函式表 ,函式表如圖1所示 正弦積分函式圖像 正弦積分函式圖像如圖2所示 有圖像可得正弦積分函式的性質有:(1...
勢能為能量的一種,具有能量量綱,在國際單位制下的單位是焦耳(J),另外在涉及到粒子物理時常用到電子伏特(eV),高斯單位制下為爾格(erg)。勢能一般使用“Ep”表示,也常使用“W”“U”和“V”。勢能是一個標量函式,當一個物體與多個物體共有勢能或共有多種勢能時,這個物體所具有的總勢能為所有勢能的...
求和項是超幾何項的級數稱為超幾何級數。超幾何級數亦稱高斯級數,是超幾何方程在單位圓內的第一解。定義 超幾何級數亦稱高斯級數,是超幾何方程在單位圓內的第一解。求和項是超幾何項的級數稱為超幾何級數,常用如下記號表示 其中 且 表示升階乘,即 。超幾何項 【hypergeometric term】超幾何項 定義在自然數上...
