基本介紹
- 中文名:高斯係數
- 外文名:Gaussian coefficient
- 所屬學科:數學(組合學)
- 別稱:高斯二項式係數
- 簡介:一類組合數
基本介紹

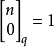
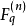
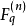
高斯係數的性質

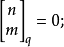




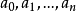

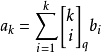




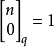
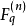
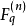

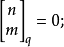




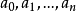

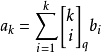


高斯係數(Gaussian coefficient)是一類組合數,設X是有限域GF(q)上的n維向量空間,X的全部k維子空間的個數稱為高斯係數,高斯係數有一系列與二項式係數相仿的等式,...
高斯整數(gaussian integer)是實數部分(實部)和虛數部分(虛部)都是整數的複數。也就是複平面中點集{a+bi|a,b 都是整數}。所有高斯整數組成了一個整環,寫作Z...
高斯引理(Gauss lemma )多項式理論的主要命題之一即任意兩個本原多項式的乘積仍是一個本原多項式。 [1] 由高斯引理可知,任一非零的整係數多項式如果能夠分解為兩...
表述地磁場的一種數學理論。1839年,C.F.高斯把球諧函式分析方法套用於地磁場,得出了地磁場的數學表達形式,奠定了地磁學的數理基礎。...
多項式的高斯引理是數論和高等代數中的一條引理,是揭示本原多項式性質的結果。指出:多個本原多項式之乘積本原。...
高斯坐標即高斯-克呂格坐標系。高斯-克呂格(Gauss-Kruger)投影簡稱“高斯投影”,又名"等角橫切橢圓柱投影”,地球橢球面和平面間正形投影的一種。...
高斯軌道(又稱高斯型軌道,英語:Gaussian type orbital,簡寫為GTO),在計算化學和理論化學中是表示原子軌道的函式,在原子軌道線性組合法中用於求算分子軌道及其性質。...
高斯—馬爾可夫定理(Gauss–Markov theory)是指在給定經典線性回歸的假定下,最小二乘估計量是具有最小方差的線性無偏估計量的這一定理。高斯--馬爾可夫定理的意義...
高斯-盧卡斯定理,又稱盧卡斯定理,該定理描述了復係數多項式的一個性質:多項式導數的根一定在原多項式的根所構成的凸包內。這一結論曾在1836被Carl Friedrich Gauss...
高斯一牛頓疊代法(Gauss-Newton iteration method)是非線性回歸模型中求回歸參數進行最小二乘的一種疊代方法,該法使用泰勒級數展開式去近似地代替非線性回歸模型,...
高斯程式(Gaussian),Gaussian是做半經驗計算和從頭計算使用最廣泛的量子化學軟體,可以研究:分子能量和結構,過渡態的能量和結構,化學鍵以及反應能量,分子軌道,偶極矩和...
數學上,高斯消元法(或譯:高斯消去法),是線性代數規劃中的一個算法,可用來為線性方程組求解。但其算法十分複雜,不常用於加減消元法,求出矩陣的秩,以及求出...
兩片新月型鏡片(meniscus-shaped)的組合,一片正一片負,這種組合就是高斯結構的...而這黏合的正鏡與負鏡使用不同色散率的係數玻璃種類(但折射率選擇約相同為1.57...
高斯-若爾當消元法(英語:Gauss-Jordan Elimination),或譯為高斯-約旦消元法,簡稱G-J消元法,是數學中的一個算法,是高斯消元法的另一個版本。它線上性代數中...
高斯-賽德爾疊代(Gauss–Seidel method)是數值線性代數中的一個疊代法,可用來求出線性方程組解的近似值。該方法以卡爾·弗里德里希·高斯和路德維希·賽德爾命名。...
這是GSM系統採用的調製方式。數字調製解調技術是數字峰窩移動通信系統空中接口的重要組成部分。GMSK調製是在MSK(最小頻移鍵控)調製器之前插入高斯低通預調製濾波器...
