基本介紹
- 中文名:離散誤差
- 外文名:discretization error
定義
誤差
減小離散誤差的方法
- 我們建立離散化模型儘可能與實際情況相符合;
- 在同一個離散化模型中,儘量避免出現剛度過分懸殊的單元,採用較密的格線分割,且注意採用較好的單元形態(儘量採用接近等邊三角形或正方形單元)。
舉例
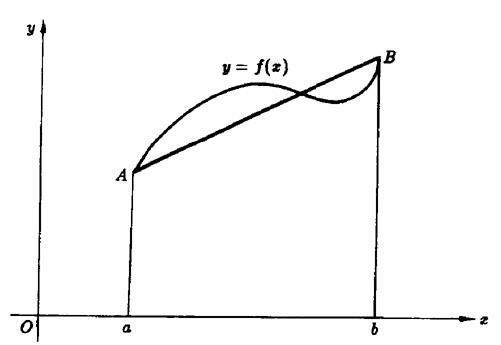


離散誤差是由於連續體被離散化模型所替代並進行近似計算所帶來的,主要是由一下兩方面引起的:一般情況下單位格線不可能精確地與連續模型的幾何形狀擬合;離散模型不能精確模擬連續體真實條件。例如在有限元分析中,離散誤差是總是存在的...
離散化誤差 離散化誤差(discretization error)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
一個量的觀測值或計算值與其真實值之差;特指統計誤差,即一個量在測量、計算或觀察過程中由於某些錯誤或通常由於某些不可控制的因素的影響而造成的變化偏離標準值或規定值的數量,誤差是不可避免的。【詳細解釋】:1.猶差錯。 漢荀悅《漢紀·文帝紀下》:“上功莫府,差六級,文吏以法繩之,陛下下之吏,削...
在構建基準模型和選定基準解的基礎上,採用熵理論建立度量誤差的模型,通過數值模擬分析各種因素對數值計算誤差的影響。構建了描述有限體積法(FVM)數值求解輻射傳輸方程(RTE)離散誤差的熵產指示因子,該方法與以往研究中選用的基於溫度場定義的誤差指示因子相比具有更好的適用性。基於信息熵理論,將RTE求解的溫升值劃分...
我們經常會碰到平均數相同的兩組數據其離散程度可以是不同的。一組數據的分布可能比較集中,差異較小,則平均數的代表性較好。另一組數據可能比較分散,差異較大,則平均數的代表性就較差。描述一組計量資料離散趨勢的常用指標有極差、四分位數間距、方差、標準差、標準誤差和變異係數等,其中方差和標準差最常用。極...
《常微分方程離散變數方法》是1985年科學出版社出版的圖書,作者是P.亨利西。內容簡介 該書共分三部分:第一部分介紹一階微分方程及高階微分方程組的單步方法,並詳細分析了這些方法的離散誤差及捨入誤差,特別是系統地闡述了捨入誤差的機率理論.第二部分討論一階及二階特殊微分方程的線性多步方法,並研究了它們的...
1 直接測量 用分軌直接表測P波的時限。誤差跟測量者讀數有關 2 計算機自動測量,能避免目測的誤差,比手工精確。臨床套用 1 P波離散度預測陣發性房顫的價值 P波離散度≥40ms時,預測房顫的敏感性達81%,特異性80%,陽性預測準確率達85%以上。其房顫的復發危險度是對照表的二倍.2 P波離散度評價抗心律失常...
誤差限是指被測物體的真實值與測量的近似值之間的最大差值的絕對值。名詞簡介 在測試過程中,無論採用何種方法,由於設備、測量方法、環境、人員的觀察等多種不可控制的偶然因素的隨機和綜合影響,總會或多或少地產生一些誤差,通常無法測出被測物體的真實值(即在某一時刻、某一位置或某一狀態下被測物體的真正...
就不確定離散系統而言,其不確定性產生的原因很多,主要包括:(1)參數的測量誤差;(2)參數的辨識誤差;(3 )參數的實際值與標稱值的偏差;(4)環境和運行條件的影響,這往往是不確定性的最重要的原因;(5)工況變動的影響;(6)人為的簡化等等。將不確定系統模型擴展到反饋控制系統設計中,控制器模型C(s)和控制...
此外,Yurkin和Maltsev在其文章中分析了DDA方法的誤差與偶極間距d的關係。作者從電磁場散射理論出發,推導出偶極離散化誤差的表達式,同時分析了正方體偶極陣列和實際散射體形狀差別造成的誤差。2007年,Penttila等人發表文章,從計算速度、記憶體消耗等方面比較了SIRRI、DDSCAT、ADDA、ZDD這4種DDA軟體各自的優劣。2007年,...
在數字計算機上對連續系統進行仿真時,首先遇到的問題是如何解決數字計算機在數值及時間上的離散性與被仿真系統數值及時間上的連續性這一基本問題。從根本意義上講,數字計算機所進行的數值計算僅僅是“數字”計算,它表示數值的精度受限於字長,這將引入捨入誤差;另一方面,這種計算是按指令一步一步進行的,因而,還...
μ的一項,稱之為人工粘性。對原偏微分方程離散後的方程稱為修正方程,通過離散數值計算得到的數值解為修正方程的精確解,但作為原偏微分方程的解,還有一定的誤差,叫為離散誤差(或截斷誤差)。人工粘性項位於修正方程中充當耗散項之前,隱含在數值解中,儘管降低了解的精度,但通常有助於提高解的穩定性。
準確度及誤差 近似解的誤差定義為近似解及解析解之間的差值。有限差分法的兩個誤差來源分別是捨入誤差及截尾誤差(或稱為離散化誤差),前者是因為電腦計算小數時四捨五入造成的誤差,後者則是計算機內數字位數限制造成的誤差。差分法是以在格點上函式的值為準 在運用有限差分法求解一問題(或是說找到問題的近似...
離散化誤差 若疊代法的數值分析算到某一程度就中止計算,或是使用一些近似的數學程式,程式所得結果和精準解不同,就會出現截尾(Truncation)誤差。將問題離散化後,由於離散化問題的解不會和原問題的解完全一様,因此會出現離散化誤差。例如用疊代法計算 3x³+4=28的解,在計算幾次後我們認為其解為1.99,...
一組數據中的最大數據與最小數據的差叫做這組數據的極差。 在統計中常用極差來刻畫一組數據的離散程度。以及表示,R=Xmax-Xmin。又稱全距或範圍誤差。反映的是變數分布的變異範圍和離散幅度,在總體中任何兩個單位的標準值之差都不能超過極差。同時,它能體現一組數據波動的範圍。例如:“早穿皮襖午穿紗”,這...
9.1離散變數法和離散誤差 9.2單步法 9.3單步法的相容性、收斂性和穩定性 9.4線性多步法 9.5線性多步法的相容性、收斂性和數值穩定性 9.6常微分方程組和高階微分方程的數值解法 第十章常微分方程邊值問題的數值解法 10.1差分方法 10.2打靶法 第十一章求線性方程組的最小二乘解的數值方法 11.1線性方程...
6.3 離散的Fourier變換 習題6 第7章 數值積分 7.1 Newton-Cotes型求積公式 7.1.1 插值求積公式 7.1.2 Newton-Cotes型求積公式 7.1.3 梯形公式和Simpson公式 7.1.4 離散誤差和數值穩定性 7.2 複合求積公式 7.2.1 複合梯形公式 7.2.2 變步長梯形公式 7.2.3 複合Simpson公式 7.3 Romberg積分法 ...
機率分布或隨機變數的標準偏差是方差的正平方根值,用符號 表示。標準偏差能反映一個數據集的離散程度,標準偏差越小,這些值偏離平均值就越少,反之亦然。機率分布反應了該隨機變數的全貌,標準偏差則表示測得值的分散性。基本概念 機率分布是機率論的基本概念之一,用以表述隨機變數取值的機率規律。為了使用的方便,...
2.1 射擊誤差分析 2.1.1 射擊精度的含義及組成 2.1.2 射擊誤差的概念 2.1.3 射擊誤差的機率密度函式 2.1.4 射擊誤差的分組 2.1.5 射擊誤差的合成與變換 2.1.6 離散誤差 2.1.7 圓機率誤差 2.2 射擊準確度分析 2.2.1 概述 2.2.2 影響射擊準確度的因素 2.2.3 射擊準確度...
標準差是方差的算術平方根。標準差能反映一個數據集的離散程度。平均數相同的兩組數據,標準差未必相同。計算公式 總體標準差:樣本標準差:標準誤差:與方差的關係:方差=標準差的平方。在實驗中單次測量總是難免會產生誤差,為此我們經常測量多次,然後用測量值的平均值表示測量的量,並用誤差條來表征數據的分布,...
離散化誤差 適合 由此可知:又因差分格式與微分方程的初值相同, 。於是可知 這說明條件 滿足時,格式(6)收斂。如果a 時,格式(11)收斂。這兩個格式稱為“迎風格式”,因為a>0時, 用向後差商代替,往上風取近似值;當a ⑤差分格式的穩定性 用一個差分格式計算 時,初值 的誤差必然要影響到以後...
標準離差與標準誤差 標準離差表示樣本數據的離散程度。標準離差就是樣本平均數方差的開平方,標準離差通常是相對於樣本數據的平均值而定的,通常用M±SD來表示,表示樣本某個數據觀察值相距平均值有多遠。從這裡可以看到,標準離差受到極值的影響。標準離差越小,表明數據越聚集;標準離差越大,表明數據越離散。標準離差...
2.3 誤差評估與格線重新劃分 2.3.1 自適應有限元格線重劃分 2.3.2 離散誤差評估 2.3.3 自適應格線改進方法 2.4 接觸與摩擦處理 2.4.1 模具系統表面的描述幾何與接觸搜尋 2.4.2 接觸力計算 2.4.3 摩擦與摩擦單元處理 3 粉末金屬成形過程中缺陷預測模型建模途徑 3.1 粉末金屬體變形特徵與粉末金屬...
相對標準偏差是一種統計度量,表明數據集相對於其平均值的離散程度。相對標準偏差是通過將數據的標準偏差除以其平均值來計算的。相對標準偏差以百分比表示,其值始終為正。相對標準偏差的解釋用於顯示數據樣本的離散度。相對標準差的值越大,數據越分散。相對標準偏差越小,數據越接近其平均值。相關概念 平均值 在日常...
主要內容為:採用基於NURBS的曲面重構方法對殼體真實的幾何缺陷點雲數據進行逆向建模,建立精確的殼體幾何模型,消除了幾何離散誤差;巧妙地結合等幾何方法研究具有精確幾何缺陷描述的殼體前、後屈曲規律以及對缺陷的敏感度;建立殼體幾何缺陷隨機場模型,結合蒙特卡洛模擬,統計屈曲載荷值的分布特徵,並進行殼體屈曲的可靠性...
2.3.2 離散卷積和離散相關 2.3.3 一些特殊序列的DFT 2.3.4 實序列DFT技術 2.4 離散正弦變換和離散餘弦變換 2.4.1 離散正弦變換 2.4.2 離散餘弦變換 2.5 離散Fourier級數 2.5.1 離散最佳平方逼近 2.5.2 離散Fourier級數 2.6 Fourier變換的離散誤差 2.6.1 離散取樣與頻譜混疊 2.6.2 有限窗寬...
《高強化柴油機結構仿真與分析》是2010年7月1日北京理工大學出版社出版的圖書,作者是左正光。內容簡介 《高強化柴油機結構仿真與分析》針對高強化柴油機結構仿真和分析中的部分關鍵問題,介紹了作者在高強化柴油機的複雜結構的功能分解與特徵建模、結構有限元計算離散誤差分析與套用、零部件模態計算建模與分析、微動作用...
精密度是指在對多個量的多次測量中,各測量值之間的離散程度。可以看出,精密度的實質在於它對數據準確度的影響,同時在很多情況下,它可以通過準確度得到體現,故常把二者結合在一起稱為精確度,簡稱精度。基本信息 對不同的規定條件,有不同的精密度的度量。最重要的精密度的度量是重複性和再現性。重複性和再現...
預測精度是指預測誤差分布的密集或離散程度,其水平取決於模型結構穩定性、外生變數預測與實際數據的精確性,以及模型設定與估計水平的精確性等。預測誤差是實際值與對應的預測值之間的離差。它的大小反映了預測的精確程度。預測誤差小,表明預測精度高;反之,表明預測精度低。既然預測會有誤差,那么怎樣判斷誤差的大小,...
本書將統計方法套用到一些較為前沿的問題中,例如離散誤差分析、模型降階等。在書中,這些統計方法還被進一步套用於一系列實際問題中,包括有限角度斷層成像、圖像去模糊、電阻抗斷層成像、生物磁學反問題等。圖書目錄 第1章反問題與對測量的詮釋 第2章經典正則化方法 第3章統計反演理論 第4章非穩態反問題 第5章...
