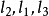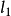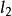雙曲型圓簇

雙曲型圓簇(hyperbolic family of circles)是圓簇的一種，指冪是正的圓簇。有公共等冪心的圓的集合叫做圓簇，又叫做共冪圓系，這公共等冪心叫做該簇的中心。等冪心對簇內每個圓的冪叫做圓簇的冪。如果圓簇的冪是正的，則稱該圓簇為雙曲線型圓簇，如果是負的，則稱該圓簇為橢圓型圓簇，如果圓簇的冪為零，則稱該圓簇為拋物線型圓簇。

基本介紹

• 中文名：雙曲型圓簇
• 外文名：hyperbolic family of circles
• 所屬學科：數學
• 所屬問題：平面幾何(圓)
• 簡介：指冪是正的圓簇

基本介紹

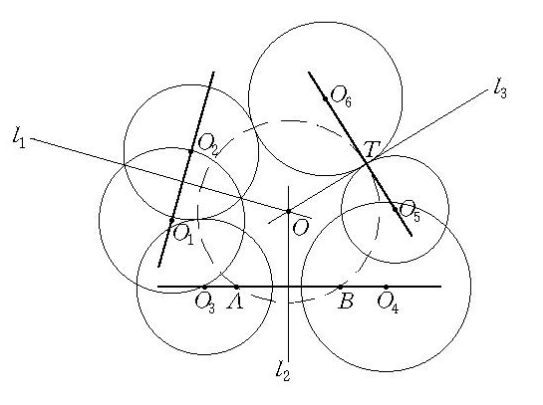
雙曲型圓簇指冪是正的圓簇。如圖1，以圓簇中心為圓心，以圓簇中心到各圓所作切線長(這些切線長均相等)為半徑的圓稱為圓簇的基圓，亦稱圓簇的根圓，它與圓簇中的所有圓都直交，圖中⊙O為該圓簇的基圓。

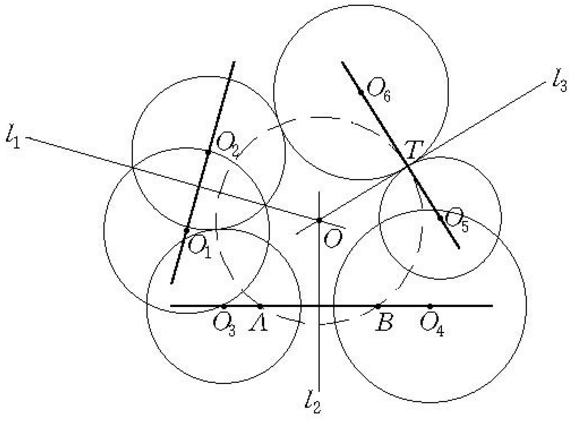圖1

雙曲型圓簇的性質

雙曲型圓簇有以下性質：

1.它的中心在圓簇中所有圓的外部.

2.圓簇中每兩個圓所確定的圓束的根軸均通過圓簇中心，形成通過這箇中心的直線束.

3.基圓與圓簇中橢圓型圓束的連心線相離.

圖中⊙O₁與⊙O₂所確定的圓束是橢圓型的，其連心線O₁O₂與基圓O相離；基圓與圓簇中雙曲型圓束的連心線相交於兩點，圖中⊙O₃與⊙O₄所確定的圓束是雙曲型的，其連心線O₃O₄與基圓O相交於A，B兩點；基圓與圓簇中拋物型圓束的連心線相切，圖中⊙O₅與⊙O₆所確定的圓束是拋物型的，其連心線O₅O₆與基圓O相切於T點。

相關介紹

在平面上存在著有公共根心的無限多的圓。根心是三個已知圓束中每兩個圓的根軸的公共交點，這個點到三已知圓的方冪相等。但因為每兩個不同的圓就確定了一個圓束， 因此三個圓心不在同一直線上的已知圓，就能確定三個不同的圓束，圓束中所有圓都有一個共同的根軸，這根軸上的點到束中所有的圓都有相等的方冪，可以想像，三個圓束的根軸的交點，它到三個圓束中所有圓都有相同的方冪。

有公共根心的圓的全體，叫做圓簇。公共的根心叫做圓簇的中心，中心對圓簇中各圓的方冪是相等的，這個值叫做圓簇的方冪。若圓簇的方冪是正的，則這個圓簇叫做雙曲型圓簇；若圓簇的方冪是負的，則叫做橢圓型圓簇；若圓簇的方冪等於0，則叫做拋物型的圓簇。

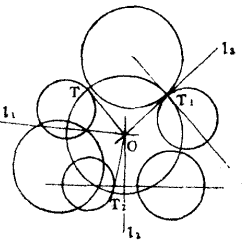圖2

對於雙曲型圓簇，簇的中心到各圓的方冪都是正的時候，就是從中心向各圓所作的切線長都等長。這樣，以中心O為圓心， 以O到各圓的切線長OT為半徑的圓，是圓簇所有圓的直交圓(圖2)，這個圓叫做圓簇的基圓。

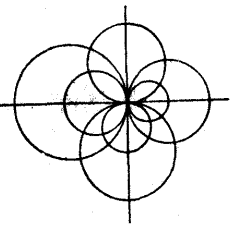圖3

我們可以推知，圓簇的中心在所有圓的外部。圓簇中每兩個圓都可以確定一個圓束，這個圓束的根軸通過中心O，形成一個通過中心的直線束。圓簇中的圓所決定的圓束可以包含雙曲、橢圓和拋物三種類型的圓束，如圖3中的根軸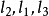就代表了這三種類型的圓束的根軸。基圓O與各圓束的連心線可以有三種關係:1)若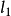是橢圓型圓束的根軸，這個圓束的公共連心線與基圓相離；2)若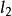是雙曲型圓束的根軸，則這個圓束的公共連心線與基圓O相交於兩個點；3)若是拋物型圓束的根軸，這個圓束的公共連心線與基圓O相切。