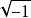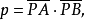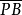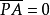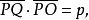基本介紹 有公共等冪心的圓的集合叫做圓簇。這公共等冪心叫做該能的中心;等冪心對於簇內每個圓的冪叫做圓簇的冪。如果圓簇的冪是正的,則該簇叫做
雙曲線 型圓簇;如果是負的,則該簇叫做
橢圓 型圓簇;如果冪等於零,則該簇叫做
拋物線 型圓族。
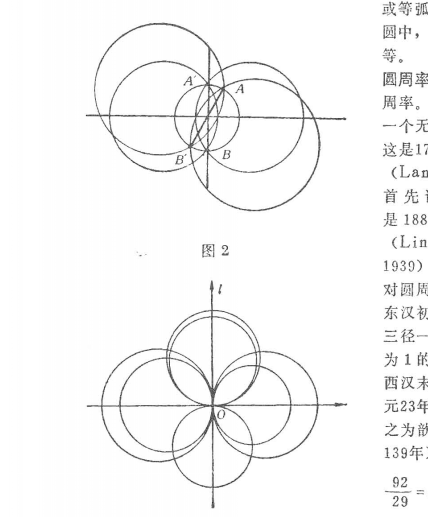
雙曲線型圓簇 圖1 圖1表示雙曲線型圓簇,圓簇的中心到簇內所有圓的切線都相等,即有一個以圖簇中心為圓心,冪的平方根為半徑的圓,圓與簇內所有圓都垂直相交,這個圓叫做雙曲線型圓簇的基圓(如圖1中的⊙O),在雙曲線型圓簇中包含著三種類型的圓束,即拋物線型圓束的等冪軸用OB表示,此圓束的連心線不與基圓相交;雙曲線型圓束的等冪軸用OC表示,此圓束的連心線與基圓相交。
橢圓型圓簇 圖2 圖2表示橢圓型圓簇,如果圓簇中心O對於所有圓的冪都是負的,則以圓簇的中心為圓心,以冪的絕對值的平方根為半徑作⊙O,於是橢圓型園簇的一切圓都交⊙O的直徑的兩端,例如AB。因此⊙O的每一直徑AB都是某種橢圓型圓束的等冪軸,而直徑的兩端是該束中所有圓的交點。由此可知,橢圓型圓簇只包括橢圓型圓束,而⊙O是圓簇中最小的圓,也是簇內各圓束所共有的圓。
拋物線型圓簇 圖3 圖3表示拋物線型圓簇,在這種情況下,簇內所有圓都應該通過簇的中心O,因為點O對於簇內所有圓的冪都等於零,所以拋物線型圈簇內有拋物線及橢圓型的圓束,而沒有雙曲線型圓束。
相關介紹 (1)設過一定點作一動直線與一定圓相交,則自定點至兩交點的兩個有向線段的積是一個常數。這是初等幾何中大家已熟知的定理,那個常數的值,我們稱它做定點對於定圓的冪;它的平方根叫做冪根,因為冪的值可為正、負或零,所以冪根的值隨著為實、虛或零,當定點在定圓的外部時,它的冪根可以用定點至定圓的切線長來表示;在圓內時,可以用過定點的極小弦的半長乘以
來表示;若在圓上,冪根的值便為零了。
上面的定義,乃係對於通常的實圓而說的,為著避免牽扯,關於虛圓的說法,我們不必去談(雖然後面也有提及虛圓的,不過只是路一提及,不去探究),以後有些地方,萬一涉及虛圓的,那就用另一方式去代替說明,除虛圓外,圓還有他種變形,譬如,半徑無窮增大而變為直線,半徑無窮減小而變為點,為著使我們的定義含義豐富,對於這些廣義的圓一直線 、無窮遠線及零圓(點)一來說,共意義仍須加以修飾一下,也可以說是規定一下;這樣對於我們以後的敘述才不會受到它們的掣肘,並且還可以使意義普遍化。
①定圓為直線,我們先這樣構想:令P為定點,自P作一直線k通過⊙O的中心而交⊙O於A,B,則P對於⊙O的冪為
而後固定點A ,使⊙O的半徑漸漸增大,即點O在k上漸趨於無窮遠,那么⊙O的極限狀態就要變成直線l的形狀,而B在k上也趨至無窮遠的位置,這時
的值便變成無窮大,這就是說,直線外的任何點對於這直線的冪是無窮大。若p在l上,即P和A相合,那么
,這時我們自然要把p看做不定值,這樣一來,當直線和圓混雜在一起而組成某某類的時候,我們就可以把直線上的點對於直線的冪看成與對於圓的冪有某種的關係(例如相等)了,這種看法在下款我們就要用到,希望讀者記著。
②定圓為無窮遠線,無論定點是通常的點或無窮遠點,一律規定它對於無窮遠線的冪是無窮大。
③定圓為零圓(點),這時定點對於零圓的冪,就用它們間的距離的平方來表示。
我們有了這些概念,直線、無窮遠線零圓和通常的圓在某種條件下的關聯便可以建立起來了。
(2)平面上兩個不同的圓,假設一個動點對於它們的冪是相等的,那么這個動點的軌跡是一條直線,這條直線就叫做那兩個圓的等冪軸.這在初等幾何中,大家一定很熟悉的了,這種特性,無論兩個圓是通常的圓抑其中有一或全是零圓,都可以適合,但若其中有一或全是直線(或有一是無窮遠線)的話,那我們仍須規定一下:
①一圓(或零圓)和一直線(或無窮遠線)的等冪軸就是那直線(或無窮遠線)的本身。
②兩直線(或有一是無窮遠線)的等冪軸是通過它們的交點的任一直線(不定)。
有了這個規定之後,那我們以後凡說圓的,都可以同時包括通常的圓、零圓、直線和無窮遠線,不再另加說明了;但有時為了使得更加明了,也不妨特別指明。
平面上許多圓,倘若它們之間兩兩的等冪鈾都相合為一,那么這許多圓所組成這樣的一群,我們就稱它做共軸圓系,這個共軸圓系的等冪軸,亦應當包括在裡面而為系中的一員,由此我們可以知道,平面上兩個不同的圓,必定完全確定一個唯一的共軸圓系。
平面上有三個不同的圓,假定它們不屬於同--的共軸圓系,那么它們便兩兩確定三個不同的共軸圓系,這三個共軸圓系的等冪軸,我們很容易知道一般都是同交於一點,只三個圓全為直線時是例外,這個點我們就稱它做那三個圓(因而也是那三個共軸圓系的全體)的等冪心;至於三條直線的等冪心我們當然認為是個不定點,現在平面上有許多圓,它們不屬於同一的共軸圓系,倘若它們之間三三的等冪心都相合為一。那么這許多圓所組成這樣的一群,我們就稱它做共冪圓系、通常地說,這個共冪圓系的等冪心對於每圓的冪必定彼此相等‘’所以我們以等冪心為圓心,等冪心對於各圓的冪根為半徑,必定作得一個唯一的圓,這個圓我們叫它做這個共冪圓系的等冪圓,再進一步說,因為冪根的值可以為實、為虛、為無窮大或為零,所以等冪圓就有實圓、虛圓、直線(或無窮遠線)或零圓等的區別。顯然,當等冪圓是實圓或直線的時候,它一定同時正交於系中的每一圓,即是它恰為系中各圓的唯一公共正交圓。
為著易於掌握共冪圓系的性質,我們要把它分成下面的幾類,如此逐類去研究,那就比較容易明了了,分類的著眼點,要從等冪圓來人手:
第一類,等冪圓為實圓,這時等冪心在系中各通常圓的外部,此類包括通常圓(圓心在等冪圓外)、零圓(等冪圓上的點)及通過等冪心的直線,也就是凡正交於一定實圓的圓,便組成第一類的共冪圓系。
第二類,等冪圓為虛圓,這時等冪心在系中各通常圓的內部,此類包括通常圓及通過等冪心的直線,設過等冪心作各圓的極小弦,則易知所得各弦都等長。而且有一個共同中點(即等冪心) ,故以各弦為直徑可作得一個唯一的圓。因此,這類共冪圓系我們也可以說是徑交於一定實圓的那些圓。
第三類,等冪圓為直線,這時等冪心為此線的垂線上的無窮遠點,此類包括通常的圓(圓心在等冪圓上)零圓(等冪圓上的點)、垂直於等冪圓的直線及無窮遠線,亦即凡正交於一定直線的圓,便組成第三類的共冪圓系。
第四類,等冪圓為零圓,這時等冪心就是等冪圓,它必定同時在系中各圓的上面,故此類共冪圓系亦即共點的一群圓,包括通常的圓、一零圓(即等冪心)及通過等冪心的直線。
第五類,等冪圓為無窮遠線,這時凡是直線及該無窮遠線的本身都屬於此類共冪圓系,這類對於上面的幾類來說,其中有一個特異的地方:把無窮遠線看做圓。圓心就不是一個固定的點。所以這類共冪圓系的等冪心應當是個不定點,因而把前幾類等冪心的唯一性的特徵消失掉了、
(3)共冪圓系經反演變換後。仍為共冪圓系。這在第一,第三。第四。第五四類來看。是很容易知道的。因為正交圓和共點圓這種屬性乃是反演不變的性質的緣故但對於第二類共冪圓 系是否也是如此呢?為要證實它一樣具有這種特性。我們可以這樣設計:假定取一點O為反演中心,設P為等冪心。P對於系中各圓的冪為p,而在OP上取一點Q,僅適合
那么通過O,Q的一群圓便組成一一個共軸圓系,這系中的每一圓顯然都屬於原來的共冪圓系,而且在後者中任取兩圓,則在前者中必有一圓與之共軸,經過反演之後,上述的那個共軸圓系的各圓便都變成共點的直線,而原共冪圓系各圓的反演圓中每兩圓的等冪軸也就不出於這些直線,於是我們的目的達到了,現在把各類共冪圓系相互間的反演變換情形列下:
①第-類經反演後,類別通常不變;但若以等冪圓上的點為反演中心,則反演為第三類。
②第二類經反演後,類別不變。
③第三類經反演後,通常變為第--類;但若以等冪圓上的點為反演中心,則類別不變。
④第四類經反演後,類別通常不變;但若以等冪心為反演中心,則反演為第五類。
⑤第五類經反演後,通常變為第四類;但若反演基圓為直線(此時等於施行線反射),則類別不變。
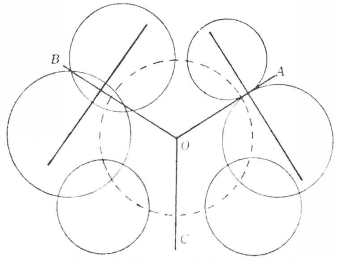 圖1
圖1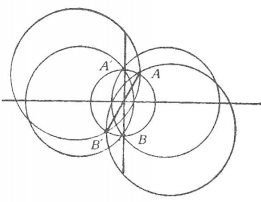 圖2
圖2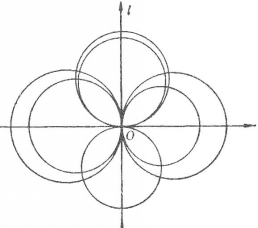 圖3
圖3