基本介紹
- 中文名:橢圓型圓簇
- 外文名:elliptic family of circles
- 所屬學科:數學
- 所屬問題:平面幾何(圓)
橢圓型圓簇的性質,橢圓型圓束,相關分析,
橢圓型圓簇的性質
橢圓型圓簇有如下性質:
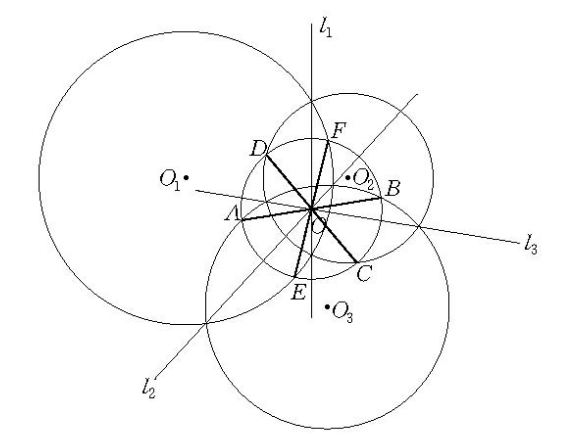
圖1
1.它的中心在圓簇中所有圓的內部。
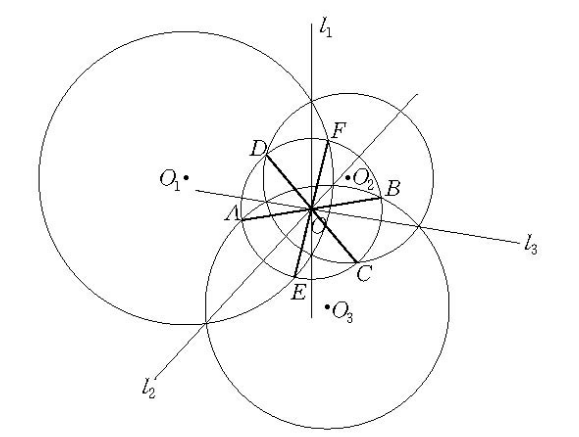
2.以中心O為圓心,以圓簇冪的絕對值的正的平方根為半徑的圓與圓簇中的所有圓相交於它的直徑的兩個端點。如圖1,它與⊙O1相交於點E,F,與⊙O2相交於點C,D,與⊙O3相交於點A,B.EF,CD,AB都是⊙O的直徑.⊙O是圓簇中最小的圓。
3.橢圓型圓簇中只包含橢圓型圓束。
橢圓型圓束
若一個圓集裡的圓兩兩的等冪軸是同一直線I,這圓集就叫做圓束,也叫做共軸圓系,l叫做圓束的等冪軸,圓束也就是同一平面內同時通過兩個定點的一族圓(這兩點可以為實點,也可以為虛點).
若已知圓束中的兩圓





若圓束中所有圓都通過其中一圓與等冪軸的兩個交點,則稱這樣的圓束為橢圓型圓束。 ·
若圓束中所有的圓都和等冪軸切於一點,則稱圓束為拋物線型圓束。
若圓束中所有的圓都和等冪軸無交點,則稱圓束為雙曲線型圓。
對於一個圓束,有無數多個圓與其中所有圓正交,這些圓之集合稱為已知圓束的共軛圓束,橢圓型圓束與雙曲線型圓束共軛,拋物線型與拋物線型圓束共軛。
利用圓束可以研究等冪軸,亦可用來解決幾何作圖問題。
相關分析
在平面上存在著有公共根心的無限多的圓。根心是三個已知圓束中每兩個圓的根軸的公共交點,這個點到三已知圓的方冪相等。但因為每兩個不同的圓就確定了一個圓束, 因此三個圓心不在同一直線上的已知圓,就能確定三個不同的圓束,圓束中所有圓都有一個共同的根軸,這根軸上的點到束中所有的圓都有相等的方冪,可以想像,三個圓束的根軸的交點,它到三個圓束中所有圓都有相同的方冪。有公共根心的圓的全體,叫做圓簇。公共的根心叫做圓簇的中心,中心對圓簇中各圓的方冪是相等的,這個值叫做圓簇的方冪。若圓簇的方冪是正的,則這個圓簇叫做雙曲型圓簇;若圓簇的方冪是負的,則叫做橢圓型圓簇;若圓簇的方冪等於0,則叫做拋物型的圓簇。
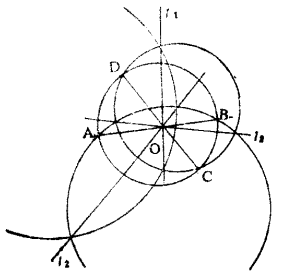
圖2
若圓簇的中心在圓簇所有圓的內部,中心O關於各圓的方冪是負的,以中心O為圓心,以圓簇的方冪的絕對值的平方根OD為半徑的圓,與圓簇中的所有圓相交於它的直徑的兩個端點,例如圖2中的點A、B或點C、D等等,點O關於所有圓的方冪都等於圓O的半徑的平方附以負號。顯然圓O每個直徑AB所在的直線,都是圓簇中兩圓所確定的一個橢圓型圓束的根軸,這直徑的兩個端點A、B是圓束中所有圓的公共交點,橢圓型圓簇只包含橢圓型圓束,圓O是圓簇中最小的圓,也是各圓所共有的圓。