基本介紹
簡介,發現者,原理,用途,二極體,相關效應,巨磁電阻效應,量子隧道效應,隧道效應套用,
簡介
由微觀粒子波動性所確定的量子效應。又稱勢壘貫穿。考慮粒子運動遇到一個高於粒子能量的勢壘，按照經典力學，粒子是不可能越過勢壘的；按照量子力學可以解出除了在勢壘處的反射外，還有透過勢壘的波函式，這表明在勢壘的另一邊，粒子具有一定的機率，粒子貫穿勢壘。理論計算表明，對於能量為幾電子伏的電子，方勢壘的能量也是幾電子伏 ，當勢壘寬度為1埃時 ， 粒子的透射機率達零點幾 ；而當勢壘寬度為10埃時，粒子透射機率減小到10^-10 ，已微乎其微。可見隧道效應是一種微觀世界的量子效應，對於巨觀現象，實際上不可能發生。在勢壘一邊平動的粒子，當動能小於勢壘高度時，按經典力學，粒子是不可能穿過勢壘的。對於微觀粒子，量子力學卻證明它仍有一定的機率穿過勢壘，實際也正是如此，這種現象稱為隧道效應。對於諧振子，按經典力學，由核間距所決定的位能決不可能超過總能量。量子力學卻證明這種核間距仍有一定的機率存在，此現象也是一種隧道效應。
隧道效應
隧道效應隧道效應是理解許多自然現象的基礎。
在兩層金屬導體之間夾一薄絕緣層，就構成一個電子的隧道結。實驗發現電子可以通過隧道結，即電子可以穿過絕緣層，這便是隧道效應。使電子從金屬中逸出需要逸出功，這說明金屬中電子勢能比空氣或絕緣層中低．於是電子隧道結對電子的作用可用一個勢壘來表示，為了簡化運算，把勢壘簡化成一個一維方勢壘。
所謂隧道效應，是指在兩片金屬間夾有極薄的絕緣層（厚度大約為幾個nm（10^-6m），如氧化薄膜），當兩端施加勢能形成勢壘V時，導體中有動能E的部分微粒子在E<V的條件下，可以從絕緣層一側通過勢壘V而達到另一側的物理現象。
hλ=-√2mE
隧道效應
隧道效應（其中，h——普朗克常數24x；m——電子質量；E——電子的動能），在勢壘V前：若E>V，它進入勢壘V區時，將波長改變為
hλ’=-√2m（E-V）
若E<V時，雖不能形成有一定波長的波動，但電子仍能進入V區的一定深度。當該勢壘區很窄時，即使是動能E小於勢壘V，也會有一部分電子穿透V區而自身動能E不變。換言之，在E<V時，電子入射勢壘就一定有反射電子波存在，但也有透射波存在。
發現者
1957年，受僱於索尼公司的江崎玲於奈（Leo Esaki，1940～）在改良高頻電晶體2T7的過程中發現，當增加PN結兩端的電壓時電流反而減少，江崎玲於奈將這種反常的負電阻現象解釋為隧道效應。此後，江崎利用這一效應製成了隧道二極體（也稱江崎二極體）。 1960年，美裔挪威籍科學家加埃沃（Ivan Giaever，1929～）通過實驗證明了在超導體隧道結中存在單電子隧道效應。在此之前的1956年出現的“庫珀對”及BCS理論被公認為是對超導現象的完美解釋，單電子隧道效應無疑是對超導理論的一個重要補充。 1962年，年僅20歲的英國劍橋大學實驗物理學研究生約瑟夫森（Brian David Josephson，1940～）預言，當兩個超導體之間設定一個絕緣薄層構成SIS（Superconductor-Insulator- Superconductor）時，電子可以穿過絕緣體從一個超導體到達另一個超導體。約瑟夫森的這一預言不久就為P.W.安德森和J.M.羅厄耳的實驗觀測所證實——電子對通過兩塊超導金屬間的薄絕緣層（厚度約為10埃）時發生了隧道效應，於是稱之為“約瑟夫森效應”。巨觀量子隧道效應確立了微電子器件進一步微型化的極限，電子就通過隧道效應而穿透絕緣層，使器件無法正常工作。因此，巨觀量子隧道效應已成為微電子學、光電子學中的重要理論。
隧道效應
隧道效應原理
經典物理學認為，物體越過勢壘，有一閾值能量；粒子能量小於此能量則不能越過，大於此能量則可以越過。例如騎腳踏車過小坡，先用力騎，如果坡很低，不蹬腳踏車也能靠慣性過去。如果坡很高，不蹬腳踏車，車到一半就停住，然後退回去。
隧道效應
隧道效應量子力學則認為，即使粒子能量小於閾值能量，很多粒子沖向勢壘，一部分粒子反彈，還會有一些粒子能過去，好像有一個隧道，故名隧道效應（quantum tunneling）。可見，巨觀上的確定性在微觀上往往就具有不確定性。雖然在通常的情況下，隧道效應並不影響經典的巨觀效應，因為隧穿幾率極小，但在某些特定的條件下巨觀的隧道效應也會出現。
用途
隧道效應本質上是量子躍遷，電子迅速穿越勢壘。隧道效應有很多用途。如製成分辨力為0.1nm（1A）量級的掃描隧道顯微鏡，可以觀察到Si的（111）面上的大元胞。但它適用於半導體樣品的觀察，不適於絕緣體樣品的觀測。在掃描隧道顯微鏡（STM）的啟發下，1986年開發了原子力顯微鏡（AFM）。利用金剛石針尖製成以SiO2膜或Si3N4膜懸臂樑（其橫向截面尺寸為100μm×1μm，彈性係數為0.1～1N/m），樑上有雷射鏡面反射鏡。當針尖金剛石的原子與樣品的表面原子間距離足夠小時，原子間的相互作用力使懸臂樑在垂直表面方向上產生位移偏轉，使入射激光的反射光束發生偏轉，被光電位移感測器靈敏地探測出來。原子力顯微鏡對導體和絕緣體樣品都適用，且其分辨力達到0.01nm（0.1A），可以測出原子間的微作用力，實現原子級表面觀測。
隧道效應
隧道效應根據光隧道效應原理，利用光纖探測頭、壓電陶瓷、光電倍增管、掃描控制跟蹤系統和微機，可以構成光隧道顯微鏡。它可以探測樣品的表面形貌。在經典物理中，光在光纖內部全反射，在量子物理中，雷射可以從一根光纖內通過隧道效應進入相距很近的另一個光纖內部，分光器就是利用量子隧道效應而製成的。
二極體
隧道二極體是一種具有負阻特性的半導體二極體。隧道二極體是採用砷化鎵（GaAs）和銻化鎵（GaSb）等材料混合製成的半導體二極體。其電流和電壓間的變化關係與一般半導體二極體不同。當某一個極上加正電壓時，通過管的電流先將隨電壓的增加而很快變大，但在電壓達到某一值後，忽而變小，小到一定值後又急劇變大；如果所加的電壓與前相反，電流則隨電壓的增加而急劇變大。因為這種變化關係只能用量子力學中的“隧道效應”加以說明，故稱隧道二極體。由於“江崎二極體”具有負電阻，並且隧道效應發生速度異常迅速，可用於高頻振盪、放大以及開關等電路元件，尤其可以用來提高電子計算機的運算速度。
隧道效應
隧道效應相關效應
巨磁電阻效應
超導隧道結的發現在理論和實驗上均有重要的價值。受此啟發Julliere對Fe/Ge/Co磁性隧道結輸運性質的研究作了開拓性的研究，發現隧道阻抗隨鐵磁層的磁化狀態而變化，低溫下電導的相對變化可達14%。1975年後人們對類似結構中的磁電阻效應進行了研究，但在室溫下均不能獲得較大的磁電阻效應。在GMR效應全球研究浪潮推動下，1994年在“磁性金屬/非磁絕緣體/磁性金屬”（FM/I/FM）型隧道結Fe/Al2O3/Fe中獲得了突破性進展。4.2K低溫下，磁電阻變化率高達30%，室溫下達18%。在這種結構中如果兩鐵磁層的磁化方向平行，一個鐵磁層中多數自旋子帶的電子將進入另一個電極中的多數自旋子帶的空態，同時少數自旋子帶的電子也從一電極進入另一電極的少數自旋子帶的空態；如果兩電極的磁化方向反平行，則一個電極中的多數子帶的自旋與另一個電極的少數自旋子帶電子的自旋平行，這樣，隧道電導過程中一個電極中多數自旋子帶的電子必須在另一個電極中尋找少數自旋子帶的空態，因而其隧道電導必須與兩極的磁化方向平行時的電導有所差別，將隧道電導與鐵磁電極的磁化方向相關的現象稱為磁隧道閥效應（magnetic valve effect）。理論上假定電子穿越絕緣體勢壘時保持其自旋方向不變，在實際製備過程中由於氧化層生成時難免導致相鄰鐵磁層氧化，致使反鐵磁性的氧化薄層的出現影響磁電電阻效應。所以實驗的結果比理論上的預計要小。
因為Fe和Co的ρ值分別為40%和34%，故Julliere模型可得Fe/I/Co的24%，但Fe/Ge/Co的實驗值與理論值有一定差距。在磁隧道閥中，磁場克服的鐵磁層的矯頑力就可使它們的磁化方向轉至磁場方向而趨於一致，這時TMR（即隧道磁電阻）為極小值；若將磁場減小至負，矯頑力小的鐵磁層的磁化方向首先反轉，兩鐵磁層的磁化方向相反，隧道電阻為極大值。由於只需反轉一個單純的鐵磁層，因而只需一個非常小的外場便可實現TMR極大值，所以其磁場靈敏度極高。Fe/Al2O3/Fe 和CoFe/Al2O3的磁場靈敏度分別為8%/Oe和5%/Oe。這些結果是多層膜的GMR及氧化物的CMR遠所難及的。另外，在磁隧道結中可以通過改變氧化層的厚度來改變零場下的電阻值，而磁隧道結電阻值並不因此而改變的。這在金屬多層膜中是很難實現的。這樣根據不同的器件的驅動電壓不同可以設計出不同的磁隧道結。今後如能解決氧化層的穩定製備和製備過程中鐵磁層的氧化問題，其工業套用前景非常可觀。此外如果技術手段可以保證的話，製備多層氧化隧道結也許可以獲得更為豐富的物理效應和套用價值。隧道結的磁電阻效應取得了突破之後，人們受顆粒膜的啟發又在Ni-SiO2， Co-SiO2， Fe-MgF2以及Fe-SiO2的鐵磁絕緣物顆粒膜中發現了高的磁電阻效應。實驗表明該體系中磁電阻效應與磁性顆粒的大小有關，數值不大，飽和場較高，套用的前景可能不大。
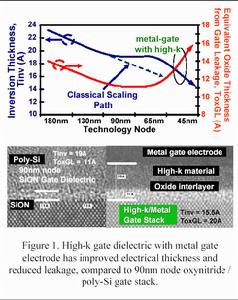隧道效應
隧道效應量子隧道效應
各種元素的原子具有特定的光譜線，如鈉原子具有黃色的光譜線。原子模型與量子力學已用能級的概念進行了合理的解釋，由無數的原子構成固體時，單獨原子的能級就併合成能帶，由於電子數目很多，能帶中能級的間距很小，因此可以看作是連續的，從能帶理論出發成功地解釋了大塊金屬、半導體、絕緣體之間的聯繫與區別，對介於原子、分子與大塊固體之間的超微顆粒而言，大塊材料中連續的能帶將分裂為分立的能級；能級間的間距隨顆粒尺寸減小而增大。當熱能、電場能或者磁場能比平均的能級間距還小時，就會呈現一系列與巨觀物體截然不同的反常特性，稱之為量子尺寸效應。例如，導電的金屬在超微顆粒時可以變成絕緣體，磁矩的大小和顆粒中電子是奇數還是偶數有關，比熱亦會反常變化，光譜線會產生向短波長方向的移動，這就是量子尺寸效應的巨觀表現。因此，對超微顆粒在低溫條件下必須考慮量子效應，原有巨觀規律已不再成立。些巨觀物理量，如微顆粒的磁化強度、量子相干器件中的磁通量等亦顯示出隧道效應，稱之為巨觀的量子隧道效應。量子尺寸效應、巨觀量子隧道效應將會是未來微電子、光電子器件的基礎，或者它確立了現存微電子器件進一步微型化的極限，當微電子器件進一步微型化時必須要考慮上述的量子效應。例如，在製造半導體積體電路時，當電路的尺寸接近電子波長時，電子就通過隧道效應而溢出器件，使器件無法正常工作，經典電路的極限尺寸大概在0．25微米。研製的量子共振隧穿電晶體就是利用量子效應製成的新一代器件電子具有粒子性又具有波動性，因此存在隧道效應。
隧道效應
隧道效應
隧道效應隧道效應套用
隧道效應──微觀粒子能透入按經典力學規律它不可能進入的勢壘區，是反映微觀粒子的波動性的一種基本效應。可以把半導體（或絕緣體）中的電子遷移現象理解為在外電場下，束縛在一個原子中的電子，通過隧道穿透勢壘，到另一個原子中。不過，通常說的半導體中的隧道效應指的不是這種對原子勢場的量子隧道效應。而是指電子對半導體中巨觀勢壘的穿透，這個巨觀勢壘是半導體的禁帶造成的。C.齊納在1934年最先提出，在外電場下,價帶的電子可以穿過禁帶進入導帶。在禁帶中電子波函式指數衰減（波矢是複數的），就和穿過勢壘時相似；齊納認為這是強場下半導體(或絕緣體)電擊穿的一種原因。但實驗表明，通常半導體電擊穿過程中，這種原因（稱齊納擊穿）只起很次要的作用。只有在某些特殊類型的PN結的反向擊穿中，才有以齊納擊穿為主的情況。這種類型的PN結稱齊納二極體，或按其用途叫穩壓二極體。通常是矽二極體。1957年江崎玲於奈發明了隧道二極體。它是高摻雜半導體形成的窄的PN結；當它加上前向偏壓時，N區電子可以通過隧道效應，穿過禁帶進入P區中價帶的空狀態。隨所加的偏壓增大，開始時隧道電流變大（可以進入的空狀態增多）；隨後到達極大值然後逐漸下降（可以進入的空狀態減少），最後下降到零（可以進入的空狀態沒有了）。隧道二極體伏安特性曲線]是隧道二極體的伏安特性曲線，以及對應各部分的PN結能帶圖。隧道二極體正向伏安特性中有一段負阻區，而且它還是一種多數載流子效應,沒有渡越時間的限制，所以隧道二極體可用作低噪聲的放大器、振盪器或高速開關器件，頻率可達毫米波段。它作為器件的缺點是功率容量太小。隧道過程中,常常有電子－聲子相互作用或電子-雜質相互作用參加。從隧道二極體的伏安特性上可分析出參與隧道過程的某些聲子的頻率。在勢壘區中的光吸收或發射中，隧道效應也起著作用，這稱夫蘭克－凱爾德什效應。雜質的束縛電子態和能帶中電子態之間的隧道也觀察到。
江崎玲於奈的發明開創了研究固體中隧道效應的新階段。因此，他和發現超導體中隧道現象的I.加埃沃、B.D.約瑟夫森一起獲得了1973年諾貝爾物理學獎。金屬半導體接觸勢壘（肖特基勢壘）中的隧道現象也很有趣。1932年，A.H.威耳孫、約飛和夫倫克耳企圖用隧道電流來解釋肖特基勢壘的整流效應，但發現所預言的整流方向是錯誤的。不過，卻發現有些高摻雜的肖特基勢壘在小的前向偏壓下，隧道電流是主要的電流機制。金屬－絕緣體－半導體系統中隧道效應的研究也是有意義的。
經濟學家Shleifer提出的“隧道效應”
Laffont他們研究的同時，Shleifer等從法律經濟學的視角出發，提出了公司治理中的“隧道效應”理論。他們的分析認為：隧道效應即控股股東為了自己的利益從公司轉移資產和利潤的行為，這一理論比較好的解釋了控股股東侵害中小股東的利益的現象。1997～1998年的亞洲金融危機提供了控股股東掠奪公司資源、侵害中小股東權益的許多案例。事實上，隧道效應不僅僅發生在新興市場，有著完善的民法的已開發國家同樣有掠奪行為，而且這些掠奪行為可能還是合法的行為；而在新興市場，隧道行為有時採取偷竊和欺詐的方式。這些理論的提出，使得合謀理論從組織間的研究，進一步拓展深入到公司治理領域；而轉型經濟中的公司治理，為合謀理論的理論和實證研究提供了一片沃土；此後的一系列相關實證研究更是進一步推動和驗證了合謀理論。
隧道效應理論主要從控股股東掠奪中小股東權益的發生機制、掠奪的手段以及司法的介入的作用等方面做了理論和案例分析，當然也有許多實證和經驗研究。但隧道效應理論在討論控股股東掠奪的時候，一般比較少涉及到管理層，特別是控股股東和管理層的合謀侵害（掠奪）中小股東權益的情形。本來，現實中，掠奪得以進行，就必然需要管理層的合謀（或者說是協助）。此外，隧道效應理論也比較少的考慮信息的作用和交易成本的影響，而是比較多的考慮了法律的作用，這也是隧道效應理論的局限所在。但是，隧道效應理論對於公司治理、特別是新興轉型國家的公司治理還是很有開創性的理論意義與實際意義的。
