超導體的單電子隧道效應，人們曾用這個方法研究了墹 隨溫度的變化關係,證明BCS理論預言的這個關係是正確的。
正文,參考書目,
正文
電子-內部結構模型圖通常把兩塊金屬電極中間夾一層很薄的絕緣層(厚度為10厘米的數量級)的結構叫做隧道結。根據量子力學原理，電子可以通過這樣薄的絕緣層。在隧道結兩端有電壓()時，能夠產生足夠大的可觀測的電流()。這是隧道效應的一種。隧道電流的大小除與絕緣層的厚度有很大關係外，還與兩個電極中電子態密度有關。電子態密度的特徵會影響隧道結的伏安特性曲線()的形狀。
當兩個電極都是正常金屬N時,在不太高的電壓（低於 1伏）範圍內（如圖中N-I-N情況）,()是一條直線。它說明，在這個範圍內，正常金屬的電子態密度是一個與能量無關的常量。
超導體的單電子隧道效應 若電極是超導體，()曲線就複雜些。超導微觀理論預言，超導體中單電子的態密度。這裡 2墹是超導體的能隙寬度。當溫度遠低於超導體的臨界溫度時，對於一個電極是超導體S的隧道結,當<墹時除了在能隙上的激發電子可以通過結外，在能隙下的大量電子都不能通過結，因而電流很小；而當塼墹時能隙下的電子可以通過結，故電流陡然上升（如圖中S-I-N 情況）。對於二個電極都是超導體的隧道結，()曲線在處有一個極大值，在處有一個極小值，而在後電流陡然上升(如圖S-I-S情況）。利用這些特點，可以很準確地測量超導體的能隙值。人們曾用這個方法研究了墹 隨溫度的變化關係,證明BCS理論預言的這個關係是正確的。
當一個電極是正常金屬而溫度接近0K時，根據理論可以證明，隧道結()曲線的微商正比於另一個電極的態密度。人們用這個原理成功地測定了幾十種超導體的態密度。實驗表明,BCS理論的態密度公式基本上是正確的。但同時發現，對於某些超導體,特別是鉛,實驗的態密度曲線上有一些很小但不容忽視的附加結構。這在BCS理論的態密度公式中是不存在的（見超導微觀理論）。
進一步的超導理論證明，當電子－聲子耦合較強時，電子態密度曲線上就會出現有效聲子態密度(ω)引起的附加結構（見強耦合超導體）。由這種具有聲子結構的電子態密度曲線可以計算出有效聲子譜(ω)。這裡，是電子－聲子耦合強度，(ω)是聲子態密度。到目前為止，人們已測定了數十種超導體的(ω)。這對於檢驗超導理論以及研究超導體臨界溫度問題都有重要的意義。
由於超導體單電子隧道效應的重要性，它的創始人I.加埃沃和半導體隧道二極體的發明者江崎玲於奈以及超導體約瑟夫森效應的發現者共同獲得了1973年的諾貝爾物理學獎。
在上述隧道效應中，電子的能量並不改變，屬於彈性隧道過程。在穿越絕緣層時，電子也可以與其他粒子相互作用而改變能量,這就是非彈性隧道過程。當絕緣層表面存在某些雜質分子時，電子可以激發它們的轉動能級或振動能級。此時,在隧道電流中,能量高於激發能的電子數會減少，使()曲線在=處產生很微小的轉折。這種轉折在()的二次微商曲線上表現為一個尖峰──譜線,人們將它稱為非彈性電子隧道譜(IETS)。為了減小熱運動所造成的譜線寬度以及提高靈敏度，IETS通常都是在4.2K以下的溫區內測得的。利用超導體作電極，可進一步提高靈敏度。IETS與紅外光譜和喇曼光譜同樣可用來辨認分子的種類，比較起來，它的靈敏度更高些，可對極微量的雜質分子進行檢測。空氣污染分析和痕量物質分析是它的重要套用領域。
電子-內部結構模型圖
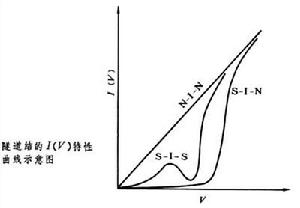超導體的單電子隧道效應
超導體的單電子隧道效應
超導體的單電子隧道效應
超導體的單電子隧道效應
超導體的單電子隧道效應
當兩個電極都是正常金屬N時,在不太高的電壓（低於 1伏）範圍內（如圖中N-I-N情況）,()是一條直線。它說明，在這個範圍內，正常金屬的電子態密度是一個與能量無關的常量。
超導體的單電子隧道效應 若電極是超導體，()曲線就複雜些。超導微觀理論預言，超導體中單電子的態密度。這裡 2墹是超導體的能隙寬度。當溫度遠低於超導體的臨界溫度時，對於一個電極是超導體S的隧道結,當<墹時除了在能隙上的激發電子可以通過結外，在能隙下的大量電子都不能通過結，因而電流很小；而當塼墹時能隙下的電子可以通過結，故電流陡然上升（如圖中S-I-N 情況）。對於二個電極都是超導體的隧道結，()曲線在處有一個極大值，在處有一個極小值，而在後電流陡然上升(如圖S-I-S情況）。利用這些特點，可以很準確地測量超導體的能隙值。人們曾用這個方法研究了墹 隨溫度的變化關係,證明BCS理論預言的這個關係是正確的。
當一個電極是正常金屬而溫度接近0K時，根據理論可以證明，隧道結()曲線的微商正比於另一個電極的態密度。人們用這個原理成功地測定了幾十種超導體的態密度。實驗表明,BCS理論的態密度公式基本上是正確的。但同時發現，對於某些超導體,特別是鉛,實驗的態密度曲線上有一些很小但不容忽視的附加結構。這在BCS理論的態密度公式中是不存在的（見超導微觀理論）。
進一步的超導理論證明，當電子－聲子耦合較強時，電子態密度曲線上就會出現有效聲子態密度(ω)引起的附加結構（見強耦合超導體）。由這種具有聲子結構的電子態密度曲線可以計算出有效聲子譜(ω)。這裡，是電子－聲子耦合強度，(ω)是聲子態密度。到目前為止，人們已測定了數十種超導體的(ω)。這對於檢驗超導理論以及研究超導體臨界溫度問題都有重要的意義。
由於超導體單電子隧道效應的重要性，它的創始人I.加埃沃和半導體隧道二極體的發明者江崎玲於奈以及超導體約瑟夫森效應的發現者共同獲得了1973年的諾貝爾物理學獎。
在上述隧道效應中，電子的能量並不改變，屬於彈性隧道過程。在穿越絕緣層時，電子也可以與其他粒子相互作用而改變能量,這就是非彈性隧道過程。當絕緣層表面存在某些雜質分子時，電子可以激發它們的轉動能級或振動能級。此時,在隧道電流中,能量高於激發能的電子數會減少，使()曲線在=處產生很微小的轉折。這種轉折在()的二次微商曲線上表現為一個尖峰──譜線,人們將它稱為非彈性電子隧道譜(IETS)。為了減小熱運動所造成的譜線寬度以及提高靈敏度，IETS通常都是在4.2K以下的溫區內測得的。利用超導體作電極，可進一步提高靈敏度。IETS與紅外光譜和喇曼光譜同樣可用來辨認分子的種類，比較起來，它的靈敏度更高些，可對極微量的雜質分子進行檢測。空氣污染分析和痕量物質分析是它的重要套用領域。
電子-內部結構模型圖超導體的單電子隧道效應超導體的單電子隧道效應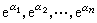超導體的單電子隧道效應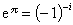超導體的單電子隧道效應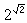超導體的單電子隧道效應參考書目
L.Solymar,Chapman & Hall, London, 1972.
管惟炎、李宏成、蔡建華、吳杭生等著:《超導電性·物理基礎》，科學出版社，北京，1981。
