基本介紹
- 中文名:除環
- 外文名:Division ring
- 領域:數學
- 別稱:斜體
- 屬性:非零環
- 相關名詞:四元數
基本信息

關係
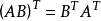
舉例



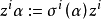


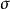

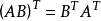



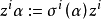


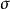
取環是指當放入子宮的環已經到了規定的年限,需要去醫院及時取出,以免環在子宮內變形或失效。取環前應先進行一次X線透視或“B”型超音波檢查。避孕環的作用就是...
在抽象代數中,除環(也稱為斜體)是一個非零環,其中每個非零元素a都具有乘法逆,即具有x·a=a·x的元素x。換句話說,一個環若且唯若單位組等於所有非零元素...
無痛取環主要是指無痛取節育環,是在麻醉下取環,具有無痛苦,起效快,無痛取環術中平穩無記憶,無痛取節育環術後清醒等特點。...
節育環是一种放置在子宮腔內的避孕裝置,由於初期使用的裝置多是環狀的,通常叫節育環,又稱宮內節育器,簡稱節育器,通常以不鏽鋼、塑膠、矽橡膠等材料製成,不帶藥...
但為使子宮內膜很好地修復,取環後,應先用其它方法避孕l~3個月後再懷孕。帶環懷孕怎么辦?以前認為帶環懷孕,環對胎兒並沒有影響,不會引起胎兒畸形,此時不必終止...
除環(division ring),又譯反稱域(skew field)、體,是如下定義的一個環: 至少有一個非零元素,這些非零元素稱為單位(Unit) 非零元素都存在逆元素(左逆元素...
稠密環(dense ring)是一類特殊環。它是除環上右向量空間的全線性變換環的一個子環,在雅各布森拓撲下,它的閉集等於全線性變換環。對並與差運算封閉的集類,測度...
線上性代數中,迪厄多內行列式是矩陣與除環和局部環上矩陣的行列式的推廣。 它是在1943年由迪厄多內提出的。...
無尾絲的節育環取出,鉗夾宮頸前唇,用探針探測宮腔深度、方向及節育器的位置,用取環鉤的鉤尖朝前,後傾、後屈位則將鉤尖朝後,鉤住節育環的下緣輕輕牽出。取...
無尾絲的節育環取出,鉗夾宮頸前唇,用探針探測宮腔深度、方向及節育器的位置,用取環鉤的鉤尖朝前,後傾、後屈位則將鉤尖朝後,鉤住節育環的下緣輕輕牽出。取...
抽象代數中,布勞威耳-加當-華定理是個有關除環的定理,以德國數學家 Richard Brauer、法國數學家埃利·嘉當、以及中國數學家華羅庚命名。...
節育環是指植入女性生殖器內的節制生育的金屬或者其它材質的環,主要是把輸卵管用節育環扎住。...
嘉當一布饒爾一華羅庚定理(Cartan-Brauer-Huatheorem)關於除環的一個著名定理.該定理斷言:除環D在它的所有內自同構下不變的子除環僅有D本身和D的中心中.嘉當(...
環路濾波器是鎖相環路中的重要組成部分, 除了濾除高頻分量外,還具有調整環路參數的作用,對於環路的捕獲特性和穩定性都具有重要作用。因取樣鑒相器鑒相增益較低, ...
顎胃動物是一類無體腔的動物,體型很小,生活在淺海細砂間,可忍受極低氧的環境,一直未被發現,是動物界至今除環口動物門以外最後被發現的一個門(1956年)。由於...
