基本介紹
設A為含n個元素的集合,A1,A2,…,Am是A的m個子集。從這m個子集中各取一元素:
ai∈Ai,i=1,2,...,m,
若排列a1,a2,…,am中無重複元素出現,則稱這樣的排列為A上的(A1,A2,…,Am)—限位排列,簡稱一個限位排列;其總個數稱為限位排列數。
限位排列實質上是對元素出現的位置加上限制的無重複排列。例如, A={1,2,3,4}的取3個元素的無重複排列,限制1不出現在第1位和第3位,2,3,4不出現在第2位。為做出這樣的排列,先做集合
所要求的排列就是(A
1,A
2,A
3)—限位排列。若取
就可做出一個(A
1,A
2,A
3)—限位排列:2 1 4。
限位排列的解法
只有一個位置或元素有限制簡稱“一限”問題,有兩個位置或元素有限制簡稱“二限”問題,“二限問題”分為混合型,無關型和影響型。
“一限”問題
方法概述
(1)解限位排列題時一般這樣分步:先排有限制的位置(或元素),再排沒有限制的位置(或元素);
(2)畫個示意圖很有益,可以分清哪個位置(或元素)有限制?這個有限制的位置上允許(不允許)安排哪些元素?這個有限制的元素允許(不允許)安排到哪些位置上?
(3)“一限”問題,先比較元素與位置的個數,一般從個數較少者著眼解題,一般有正反兩種解法,其實,從對應角度看,元素、位置並沒有區別。
例題解析
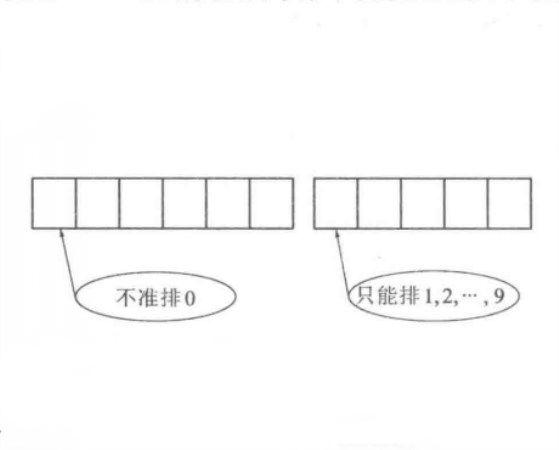
【例1】用0~9這10個數字,可以組成多少個沒有重複數字的五位數?
解:畫出下列示意圖(如圖1),首位有限制:不準排0。
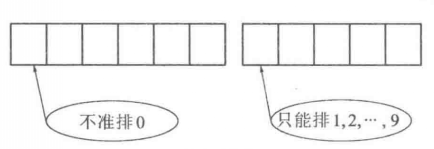
圖1
方法1:(正面解)先排首位,有
種方法,假定首位排1,再排後面4個位置,有2,3,…,9,0這9個元素.因此有
種方法。(假定首位排2,或者3,4,…,後面4個位置,都同樣有
種方法)。於是,根據分步的乘法原理,總共有
×
=27216(種)方法。
方法2:(反面扣除)首位排0總共有
種方法,但這是不合要求的,予以扣除,所以共有
-
=27216(種)方法。
【例2】有3封不同的信件甲、乙、丙,現要將它們分別投人五個編號分別為1、2、3、4、5的信箱,其中甲信件不能投入1號信箱,且每個信箱最多投入一封信件,共有多少種不同的投法?
分析 上例是從元素和位置的個數來講,供選擇的元素個數(10個)多於所需填空的位置數量(5個),因此我們比較推薦從位置著眼,本例中信件作為元素(3個),信箱作為位置(5個),有限制的元素是甲信件,有限制的位置是編號為1的信箱,在數量上元素少於位置,此時如果從位置著眼的話就涉及到先分類,再分步,因此我們這裡推薦從元素著眼:先將甲信件投入編號為2,3,4,5的四個信箱中的一個,有
種投法;再將乙、丙兩封信件分別投入剩下的四個信箱中的兩個,有
種投法,如圖2,根據乘法原理,總共有
×
(種)投法。
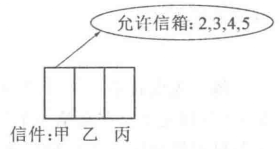
圖2
“二限”問題
方法概述
“二限”問題可以有三種情況:無關型,影響型,混合型。
(2)建議還是先畫示意圖,構造出這兩個位置上分別允許排的元素的集合,再考察這兩個集合間的關係,如果交集為空集,則是無關型;如果有包含關係,則是影響型;如果是部分交叉關係,則是混合型。
(3)無關型的二限排列題,先安排哪個有限制的位置都可以;影響型的題,則先安排包含關係里的子集相應的位置較合適,如果反之,則把該題當作混合型來解了,把問題複雜化了;混合型的題,可以先分類:把該題分拆為一個無關型和一個影響型的題來解,次序上沒有關係。
(4)“二限”問題不建議從反面解。
例題解析
【例3】在6000到9000之間有多少個沒有重複數字的5的倍數?
分析 限制條件是千位上只能安排元素6,7,8;個位上只能安排元素0,5。

圖3
畫出示意圖(如圖3),注意到個位和千位有限制,是所謂的“二限”問題,並且注意到個位、千位上允許排的元素不重複(集合{6,7,8}∩{0,5}≠∅)。先安排千位,再安排個位(這個順序可以倒過來),最後安排中間兩位。
解 千位上的排法是
,個位的排法是
,所以總共有
(種)排法。
【例4】從A、B、c、D、E、F、G 7位歌手中選4位表演獨唱,規定每位歌手最多只能出場一次,而且第一個節目不能排A、B,第二個節目不能排A、B、C、D。問:有幾種排法?
分析 這題目有兩個限制條件:第一個節目和第二個節目,第一個節目不能排A、B,能夠排的是C、D、E、F、G,第二個節目不能排的是A、B、C、D,能夠排的是E、F、G。
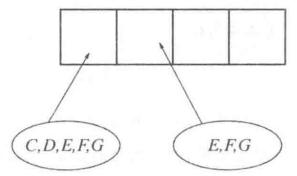
圖4
畫示意圖(如圖4),可知第一個節目允許安排的歌手組成集合{C,D,E,F,G},第二個節目允許安排的歌手組成集合{E,F,G},它們之間有包含關係:{E,F,G}⊊{C,D,E,F,G}。
解 先安排第二個節目,有3種可能;再安排第一個節目,不管第二個節目裡安排的是誰(譬如是E),那么第一個節目只有4種可能(C、D、F、G),注意:不是5種可能,受第二個節目安排的影響了!(此類是影響型。)最後餘下的5個歌手中選2個安排在第三、四個節目就行了,即3×4×
(種)。