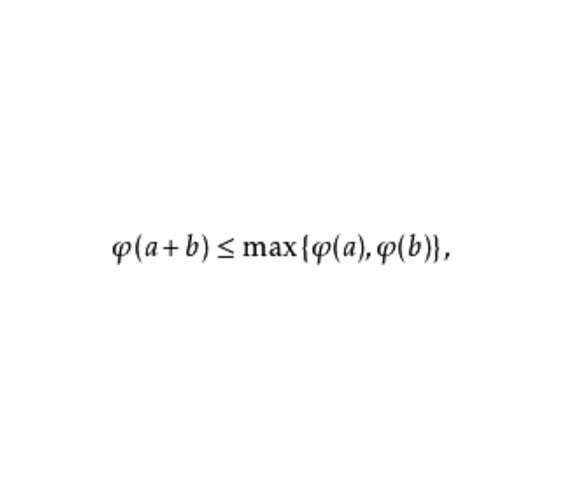阿基米德絕對值

概念基礎

賦值論

域論的一個重要分支，它是研究交換代數的一個墓元工具，特別是在代數數論、分歧理論、類域論和代數幾何中有極為估喇再重要的套用。通常的賦值可分為加法與乘法賦值兩類，有時簡去趨悼拘稱賦值。從賦值出發，可以給原來的域一個拓撲結構，使之成為拓撲域。賦值理論肇始於屈爾沙克於1913年發表的論文。賦值、賦值域這些名詞都是他首先引入的。氣候，經過奧斯特洛夫斯基（Ostrowski，A.M.）等人的工作，解決了屈爾沙克在論文中提出的問題，並發展了這一理論。1932年，克魯爾（Krull，W.）發表了題為《一般賦值理論》的基本論文，從而奠定了賦值論這一分支的基礎。時至今日，賦值理論已逐漸越出了“域”的界限，在許多代數結構上，例如群、環、向量空間等，也用多種方式引進賦值，並由此對屑說捉這些結構作算術理論的研究。此外，賦值論還滲入泛函分析的領域，發展了所謂非阿基米德泛函分析。

絕對值

一個域到實數域內的一種映射。它是通常絕對值的推廣。若φ是由域F到實數域R的映射，稱φ為F上的一個絕對值，若φ滿足條件：

1、φ(a)≥0，φ(a)=0，若且唯若a=0（F的零元）；

2、φ(ab)=φ(a)φ(b)；

3、φ(a+b)≤Cmax{φ(a),φ(b)}，其中a，b∈F，C為一常數，滿足0<C≤2；

注意由條件1,2,3可推出三角不等式，即

4、φ(a+b)≤φ(a)+φ(b)；

並且條件1,2,3與條件1,2,4是等價的。最常見的絕對值有：通常實數域的絕對值|·|，複數域上的模。