基本介紹
- 中文名:門限回歸模型
- 外文名:Threshold Regressive Model
- 簡稱:TR模型或TRM
- 提出者:湯家豪
- 所屬學科:數學(統計學)
門限回歸模型的基本思想
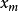
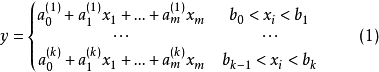

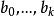
門限回歸模型的建模方法

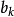
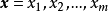
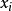
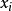
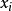

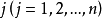
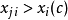
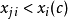

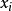

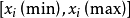
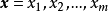
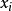
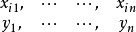
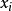
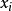
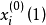
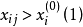
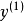
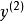
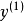
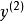

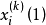

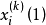

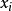

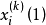
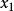
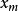
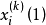

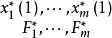
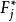
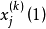


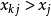
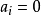
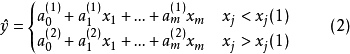
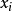


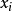
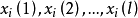
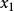
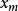



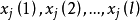
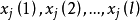

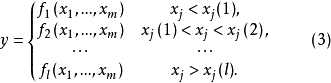



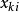


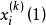

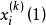


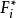

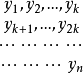
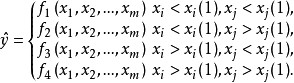
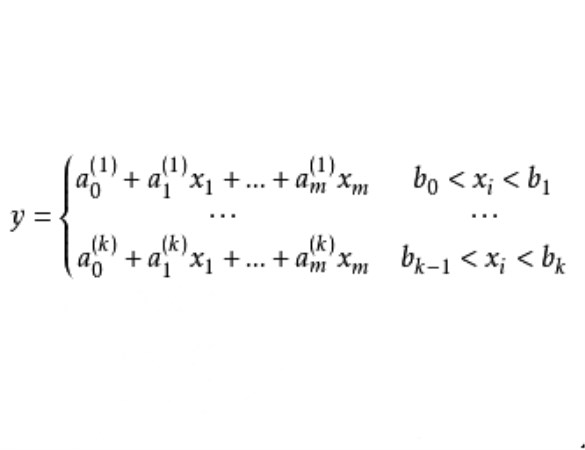
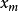
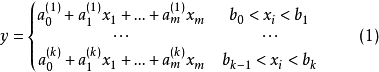

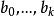

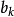
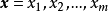
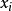
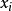
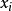

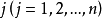
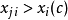
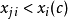

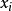

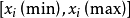
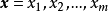
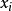
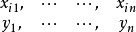
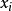
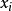
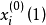
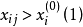
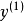
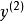
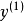
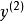

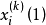

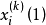

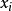

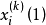
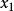
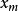
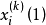

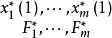
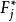
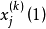


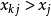
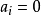
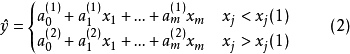
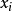


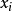
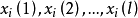
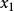
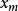



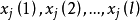
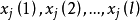

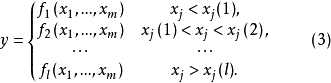



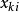


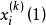

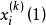


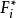

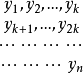
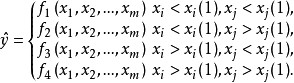
門限回歸模型(Threshold Regressive Model,簡稱TR模型或TRM)是湯家豪於1978年提出了門限自回歸模型後進一步將這一思想擴展到回歸模型中。門限回歸模型的基本思想是...
門限自回歸模型(threshold autoregressive model),又稱閾模型,簡稱TAR模型,它是一種非線性模型。門限自回歸模型由湯家豪(Tong)1978年提出,用來解決一類非線性問題。...
拐點則是指時間序列從上升趨勢突然變為下降趨勢的點。如果存在拐點,則在建模時必須用不同的模型去分段擬合該時間序列,例如採用門限回歸模型。...
如果存在拐點,則在建模時必須用不同的模型去分段擬合該時間序列,例如採用門限回歸模型。③辨識合適的隨機模型,進行曲線擬合,即用通用隨機模型去擬合時間序列的觀測...
如果存在拐點,則在建模時必須用不同的模型去分段擬合該時間序列,例如採用門限回歸模型。 辨識合適的隨機模型,進行曲線擬合,即用通用隨機模型去擬合時間序列的觀測...
擴展內容,包括多元時序的ARMAV模型,非平穩時序的各種模型非線性時序模型中的門限自回歸模型和雙線性模型,非高斯時序的各種模型,時間序列的狀態模型以及這些模型的工程...
選擇STAR模型對中國實際匯率非線性態勢進行實證預測研究的原因是:平滑轉移自回歸模型不用像馬爾可夫機制轉換模型那樣需要提出預先假設、捕捉不到狀態的變化;同時門限模型...
附錄A 估計波動率模型的一些RATS程式練習題參考文獻第4章 非線性模型及其套用4.1 非線性模型4.1.1 雙線性模型4.1.2 門限自回歸模型...
第一步,進行協整回歸(OLS法),檢驗變數間的協整關係,估計協整向量(長期均衡關係...基於門限向量誤差修正模型的中國與國際有色金屬期貨價格關聯性研究[J]. 系統...
結合貝葉斯分位回歸方法對面板門限協整模型進行參數估計,得到條件分位函式後驗估計量的解析表達式,同時,利用MCMC算法對協整模型的參數進行估計,計算出協整檢驗的後驗...
參數估計、模型診斷、預測、季節模型、時間序列回歸模型、異方差時間序列模型、譜分析入門、譜估計、門限模型.對所有的思想和方法,都用真實數據集和模擬數據集進行了...
異方差模型;第七章是向量自回歸模型;第八章是其它回歸模型,包括排序選擇模型、二元離散選擇模型、審查回歸模型、“截斷”問題的計量經濟學模型、門限回歸模型、轉換...
10. 李玉潔,繆柏其,葉五一,套用門限分位點回歸模型估計VPIN條件下CVaR,中國科學技術大學學報,2013,43(12):997-10039.葉五一,繆柏其,吳遵,套用匹配方法分析“兩職...
、協整)、自然實驗、重複截面數據、GMM、自助法、蒙特卡羅法、分位數回歸、門限回歸、非參數估計、處理效應、空間計量、久期分析、貝葉斯估計等均做了較深入的分析...
1.3.5arima模型1.4 什麼是非線性時間序列?1.5 非線性時間序列模型1.5.1一個簡單例子1.5.2arch模型1.5.3門限模型1.5.4非參數自回歸模型...
如今的湯家豪依然很忙。他一邊繼續完善門限自回歸模型,一邊還和年輕人一起研究時間序列分析的“半參數方法”。對湯家豪來說,從事數理統計的研究已經成為一種樂趣。...
第六節 門限自回歸模型參考文獻第六篇 地理模糊問題第十四章 模糊數學方法第一節 模糊聚類分析第二節 模糊綜合評判方法第三節 模糊模式識別...
為了解決這個問題,在過去的十多年中,一些學者提出了適用於非線性時間序列的分析、預測方法。如H.Tong於1978年提出的門限自回歸模型等,即首先辨識出各數據間的關係...
10.1.5 ARIMA模型的R語言實現 36710.1.6 R語言forecast包的套用 37310.2 門限自回歸模型 37610.2.1 TAR模型的基本原理 37610.2.2 TAR模型的R語言實現 ...
第20章 似不相關回歸第21章 聯立方程模型第22章 非線性回歸與門限回歸第23章 分位數回歸第24章 非參數與半參數估計第25章 貝葉斯估計簡介...
