門傑空間是規定了三角範數且滿足門傑廣義三角不等式的機率度量空間。
基本介紹
- 中文名：門傑空間
- 外文名：Menger space
- 適用範圍：數理科學
簡介,三角範數,機率度量空間,
簡介
門傑空間是規定了三角範數且滿足門傑廣義三角不等式的機率度量空間。
設(E,F)是機率度量空間，△是一個三角範數。若成立下述傑廣義三角不等式，即：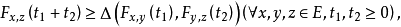
則稱(E,F,△)為門傑機率度量空間，簡稱門傑空間。
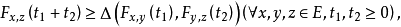
三角範數
三角範數亦稱t範數，是一種定義在正方形上在單位閉區間中取值的具有特殊性質的函式，它是研究機率度量的三角不等式的重要工具。
三角範數指的是滿足下述條件的函式△:[0,1]×[0,1]→[0,1]：
1.△(a,1)=a，△(0,0)=0。
2.△(a,b)=△(b,a)。
3.△(c,d)≥△(a,6)，當c≥a,d≥b。
4.△(△(a,b),c)=△(a,△(b,c))，其中a,b,c,d∈[0,1]。
機率度量空間
（probabilistic metric space，簡記為PM-空間）
機率度量空間亦稱門傑機率度量空間，它是度量空間的一種重要推廣，是指度量空間把兩點間距離用一個統計量描述的一種空間。
通常的度量取值於非負實數集，而機率度量取值於分布函式集。1942年，K.Menger提出PM-空間以來，一直進展很慢，直到20世紀60年代，B.Schwweizer、A.sklar等研究了其拓撲結構，才使得這一理論有了較快的發展，但目前仍有大量的問題有待研究。
