基本介紹
- 中文名:量子位
- 外文名:qubit
- 性質:基本單位
- 類型:雙態量子系統
- 基於:矽材料內的單個原子製成量子位
簡介
定義
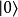
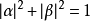


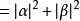

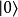
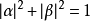


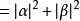

量子信息學中,基本單位是量子比特或稱為量子位,量子位是一個雙態量子系統,這裡的雙態指的是兩個線性獨立態。...
量子位能,即量子勢能(Quantum Potential)是德布羅意量子力學的中心概念型式,在1952年首度由戴維·玻姆(David Bohm)所提出。隨後在1975年由Bohm和Basil Hiley詮釋為...
量子計算是一種遵循量子力學規律調控量子信息單元進行計算的新型計算模式。對照於傳統的通用計算機,其理論模型是通用圖靈機;通用的量子計算機,其理論模型是用量子力學...
《多量子位量子糾纏及套用 》是由惠小強著,岳瑞宏指導的論文。...... 《多量子位量子糾纏及套用 》是由惠小強著,岳瑞宏指導的論文。副題名外文題名...
概念介紹量子線路或沿用古典稱呼而稱作量子電路,是在抽象概念下,對於量子信息儲存單元(例如量子位元)進行操作的線路。組成包括了於量子資訊儲存單元、線路(時間線),...
在IBM的龍華實驗室里,班奈特(Charles Bennett)是位知名而優秀的理論學家,也是量子計算這個新領域的創始者之一。就像其他多數理論學家一樣,他待在實驗室的經驗並...
在量子計算,特別是量子線路的計算模型裡面,一個量子門 (Quantum gate,或量子邏輯門)是一個基本的,操作一個小數量量子比特的量子線路 。它是量子線路的基礎,就像...
《量子計算機研究》是2011年科學出版社出版出版的圖書,作者是李承祖。本書主要介紹了包含學科主要基礎理論,又系統介紹了當前該領域前沿主要研究方向和動態。...
量子線路受控反閘(controlled-NOT gate, CNOT)出現在量子線路,是量子版本的邏輯門的一種,牽涉到兩個量子位元間的運算。...
通過測量或與其它物體發生相互作用而呈現出“ 0” 態或 “ 1” 態.任何兩態的量子系統都可用來實現量子位,例如氫原子中的電子的基態(gro und state)和第 1 ...
《量子計算機研究(上):原理和物理實現》為上冊,內容包括計算機從經典到量子、量子位和量子邏輯門、量子算法、量子計算機動力學模型、離子阱量子計算機、基於半導體量子...
在量子力學中,量子信息(quantum information)是關於量子系統“狀態”所帶有的物理信息。通過量子系統的各種相干特性(如量子並行、量子糾纏和量子不可克隆等),進行計算...
量子導航定位系統(QPS),是英國國防科學與技術實驗室(DSTL)正在研究的一種以超冷原子為基礎的加速計,它能前所未有地精確跟蹤人體移動的位置。...
全息原理是 “一個系統原則上可以由它的邊界上的一些自由度完全描述”,是基於黑洞的量子性質提出的一個新的基本原理。其實這個基本原理是聯繫量子元和量子位結合的...
全息原理,“一個系統原則上可以由它的邊界上的一些自由度完全描述”,是基於黑洞的量子性質提出的一個新的基本原理。其實這個基本原理是聯繫量子元和量子位結合的量子...
其次,類似N數量子元和N數量子位的二元排列,與N數行和N數列的行列式或矩陣類似的二元排列,其中有一個不相同,是行列式或矩陣比N數量子元和N數量子位的二元排列少...
量子力學中,以自旋物理與核磁共振專家費利克斯·布洛赫(Felix Bloch)姓氏命名的布洛赫球面是一種對於雙態系統中純態空間的幾何表示法。在討論量子位元的場合上常常...
Qubit,即量子位 (量子計算器中的最小信息單位),出處計算機量子物理。在量子信息理論中,量子信息的基本單位是量子bit(qubit,複數qubits),稱為量子位。一個qubit是...
全息原理是“一個系統原則上可以由它的邊界上的一些自由度完全描述”,是基於黑洞的量子性質提出的一個新的基本原理。其實這個基本原理是聯繫量子元和量子位結合的...
