簡介
套用
斯托克斯理論研究地球形狀。需要知道大地水準面上的重力異常△g,即要求把地球表面上觀測的重力歸算到大地水準面上,而且要求大地水準面外不存在物質。這就需要對地球進行調整,使其全部質量都歸入到大地水準面內部去,然後將實測重力值歸算到大地水準面上。顯然,質量的移動將使重力值和大地水準面形狀都發生變化。人們要求在質量移動時,地球的總質量、質心位置和大地水準面形狀都保持不變。直到目前為止,還沒有全面徹底的解決方法,只是各個學者從不同的觀點出發,提出了各人的歸算方法,而這些方法又都有各自的優缺點。下面簡述幾種常用的歸算方法。
歸算方法
空間改正
空間改正是將海拔高程為h的重力點P上的重力值g歸算為大地水準面上P
0點的重力值g
0(圖1)。歸算時不考慮地球表面和大地水準面之間的質量,只考慮高程h對重力的影響。設重力在沒有質量的自由空間的垂直梯度為∂g/∂h,則把地面上的重力值g歸算為大地水準面上P
0點的重力值g
0的空間改正為:
 圖1
圖1 由於實際重力垂直梯度並不知道,通常用φ=45°處的正常重力垂直梯度∂g/∂h=-0.3086mGal/m,於是:
式中h以m為單位。
將地麵點的重力觀測值g加上空間改正△1g後,再與正常橢球面上的正常重力值γ,相減,得:
稱為空間重力異常,它的數值與地面重力異常相差極其微小,但兩者概念不同。
布格改正
空間改正沒有顧及地面和大地水準面之間的質量對重力的影響。這一層間質量對地麵點P的重力影響的改正,稱為層間改正。現在要把這一層間質量去掉;沒有這一層質量,地麵點的重力值顯然要減小,故層間改正為負值。
 圖2
圖2現在推導地麵點P的水平面與大地水準面之間的質量對P點的引力。因為遠離P點的地區對P點的引力影響不大,而在P點的鄰近,地球的曲率可不考慮。因此,可以假設這一質量層不是球層,而是密度為δ的均質圓柱層(圖2)。在此圓柱層中取一質元dm,它對P點的引力在重力方向上的分量為:
;對於厚度為h、半徑為a的整個圓柱體的質量來說,它對P點的引力為:
地球表面上的重力值,可以近似地看成是一個半徑為R的均質圓球的引力,即:
取g=980 000mGal,R=6371km,
=5.52 g/cm
3,則得F
z=0.0418
hδ。由於層間改正是去掉這一部分引力。故:
式中δ以g/cm3為單位,h以m為單位,Δ2g以mGal為單位。δ通常採用2.67g/cm3,則層間改正為:
通常將層間改正和空間改正之和稱為布格改正,即:
局部地形改正
在進行布格改正時,認為計算點P的周圍是平坦的,且物質的密度相同。實際情況並非如此,特別是在丘陵區和山區。設P點周圍的地形分布如圖3所示,若視該點周圍地形是平坦的,只加層間改正,則質量m1和m3對P點的引力就沒有去掉,而原來不存在的質量m2和m4卻被認為對P點有引力,並把它們扣除了。這樣就必然引起誤差。為此,必須先扣除質量m1和m3的引力,並補上質量m2和m4的引力,然後再加層間改正。這種去掉高出P點水平面的質量和補上P點水平面之下缺少的質量所應加入的改正,稱為局部地形改正,以Δ
3g表示。由於高出P點水平面的質量對P點的引力(例如F1)向上,它使P點的重力減小,而去掉這些質量應使P點的重力增大;P點水平面下沒有質量的地方要填進質量,它對P的引力(例如F4)向下,使重力增大。所以不論周圍地形是高出P或低於P,局部地形改正總是正值。
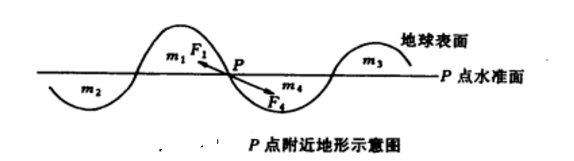 圖3
圖3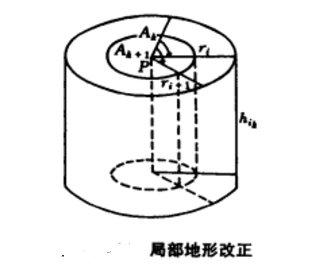 圖4
圖4如圖4,以計算點P為中心,以不同的半徑ri作圓柱面,將周圍地形質量劃分為圓環柱體。又過P作一些輻射線,將每個圓環柱體等分為n塊梯形柱體。第i個圓環第k個梯形柱體引起的局部地形改正為:
式中A
k和A
k+1為該梯形兩側輻射線的方位角,而:
r
i和r
i+1為梯形柱體的內、外半徑,h
ik為該梯形柱體相對於計算點P的平均高差。積分上式得:
n
i為第 i 環等分的梯形數。總的局部地形改正為:
將局部地形改正與布格異常相加,即得“精化的”布格異常。局部地形改正在平坦地區可達0.1~1.0mGal,在高山地區則可達10~100mGal。
如果地面觀測的重力值g只加入空間改正和局部地形改正,再減去正常橢球面上相應的正常重力值,則得出法耶異常:
地殼均衡改正
現有三種地殼均衡模型,其中以普拉特-海福德模型比較簡單,適用於重力歸算。這一模型認為,海面以下某一深度D處有一等壓面,稱為抵償面;若將地殼分割成許多截面相等的柱體(圖5),各柱體的質量是相等的。各柱體海面以上的部分,物質密度是地殼平均密度δ;海面以下的部分,物質密度小於δ,假設為
稱為抵償密度。
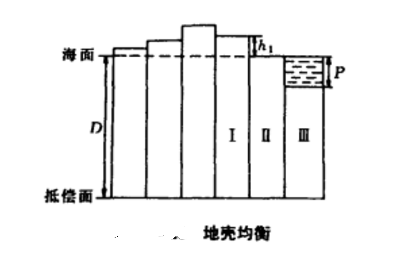 圖5
圖5容易看出,對觀測重力值加入均衡改正,就是求出各個柱體的抵償密度為δ0的質量對計算點的引力;因此,只要在第i個圓環第k個梯形柱體引起的局部地形改正公式中將z的積分限從0到hik換為從h到h+D,h為計算點P的高程。將地殼的平均密度δ換成抵償密度δ0,則可直接得出大陸地區的均衡改正公式:
式中n
i為第 i 環等分的梯形數;h
ik為第 i 環第 k 個梯形柱體高出海面的平均高程。
對於大陸來說,均衡改正是將海面以外的質量移到海面至抵償面之間,使之成為均質厚層,所以應該在觀測重力值中加上它。對於海洋地區來說,均衡改正計算公式相同,僅抵償密度不同。
觀測重力值加入空間改正、局部地形改正、層間改正和均衡改正,再減去正常橢球面上相應的正常重力值,即得均衡異常:
算法比較
現在比較上述4種重力歸算方法的優缺點,看哪一種方法最能符合前面所提出的調整後地球的以下要求:
(1)大地水準面外沒有質量;
(2)不改變地球質心位置;
(3)地球總質量不變;
(4)不改變大地水準面形狀。
下列符號表示歸算後的重力值:
觀測重力:g;
經空間改正後的重力: g空=g+Δ1g;
經法耶改正後的重力: g掛=g+Δ1g+Δ3g;
經布格改正後的重力: g布=g+Δ1g+Δ2g或g布=g+Δ1g+Δ2g+Δ3g;
經均衡改正後的重力: g均=g+Δ1g+Δ2g+Δ3g+Δ4g;
4種歸算方法的物理意義:如圖6所示,其中(a)表示P點的觀測重力值;將此值加上空間改正後,相當於將P點下降到海面MM上,但不改變影響P點的地殼質量引力,這就好像把高出海面的質量按原來的狀態壓入海面內。(b)是與g
空相應的圖;在g
空再加上局部地形改正後,相當於將P點周圍地形除去凸出部分和填平凹下部分,使得P點周圍形成平坦地形,所以g
法相當於圖中的(c)。當重力點離開平面層的距離和平面層的半徑比起來很小時,平面層的引力與重力點到層面的距離無關,因此可將厚度為h的平面層分為無限薄的許多層,並將它們全部壓縮成一片無限薄的平面層,這樣對P點的引力作用不變,這就相當於圖中的(d),所以(c)和(d)的意義是一樣的。重力觀測值加上布格改正,相當於將高出大地水準面的平面層的質量移開,即相當於圖(e),再經過均衡改正後,相當於地球自然表面和海面相合;將地形質量填補在海面與抵償面之間,使地殼構造均勻,這時P點在海面上的重力為g
均,如圖(f)。
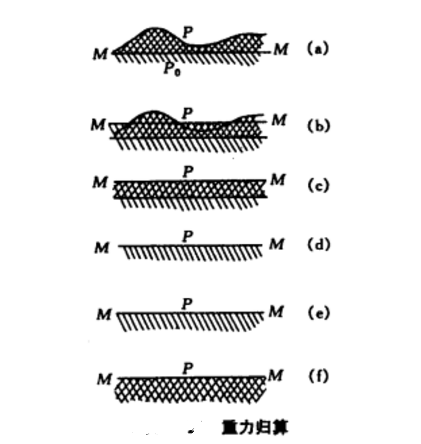 圖6
圖6現在比較上述4種歸算方法。法耶改正(空間改正加上局部地形改正)相當於將外部質量壓縮到大地水準面上,成為平面層。布格改正相當於將這個平面層的質量去掉,不作任何抵償,這樣顯然會使地殼質量不足,因而經過布格改正後的重力異常大多是負值。均衡改正是將海面以外的質量壓入海面下,而且調整地殼內部的密度以抵償大陸的質量,一般使重力異常減小,而且變化比較均勻。由於這幾種歸算都是將地球質量作了一些調整,因此大地水準面都有變化;其中布格改正是將大地水準面外的質量去掉,不作任何抵償;均衡改正較大地調整了地球的質量分布;所以這兩種改正使大地水準面有很大形變。利用法耶改正和均衡改正,地球總質量不變;布格改正則改變了地球總質量。最後,不論哪一種歸算方法都使地球質心位移。關於調整後的大地水準面位移,已作了粗略估算,結果表明。經過空間改正的重力異常引起的大地水準面形變最小,計算也簡單,適用於地球形狀和重力場的研究;缺點是和地形明顯相關,重力異常內插和外推都有困難。布格異常和均衡異常由於對地球質量作了較大的調整,引起大地水準面的明顯畸變,不適用於地球形狀及其重力場的研究;但它們對於研究地殼構造具有重要意義,而且由於顧及了地形影響,變化比較平緩,適用於計算平均異常以及重力異常的內插和外推,可用於大地測量。
 圖1
圖1



 圖2
圖2












 圖3
圖3 圖4
圖4





 圖5
圖5

 圖6
圖6
