空間改正是將海拔高程為h的重力點上的重力值g歸算成大地水準面上P0點的重力值g0。歸算時不考慮地球表面和大地水準面之間的質量，只考慮高程h對重力的影響。
由於微重力測量完全是相對於一任意參考高程(基點的高程或甚至是在大地水準面的或平均海平面的高程)的，而且只需要相對於參考高程的測點高程。所以，空間校正公式為： △gZFA=±308.55Δh(微伽) ，式中Δh為需要校正的測點和參考高程之間的高程差，以米作單位，“+”號是用於比參考高程高的測點，而“-”號則用於低的測點。
基本介紹
- 中文名：空間改正
- 外文名：Spatial correction
- 作用：重力歸算所加的改正
- 重力場：按地面重力觀測點高程考慮
簡介,空間改正的推導,自由空間改正,
簡介
在確定大地水準面形狀的基本原理中，有兩個前提，一個是大地水準面外部必須沒有質量，另一個是所用的實測重力值g應當是大地水準面上的數值g0，但事實上大地水準面外部有大陸存在，而觀測也是在地面上進行的。為了滿足上述要求，必須將地球進行一些調整，使得全部質量都包含在大地水準面內部；同時將重力值歸算到大地水準面上，然後再來確定大地水準面形狀。由於進行了調整，因此可稱這樣確定出來的大池水準面為調整後的大地水準面形狀，或調整後地球形狀。
調整後地球與真正地球的區別就是將所有高出大地水準面的質量去掉，將它們移到大地水準面內部或大地水準面下面某一位置。但是在移動質量的時候應考慮到不要改變地球的總質量、質心位置以及大地水準面的形狀。目前雖然歸算方法很多，但沒有一種歸算能符合所有要求。
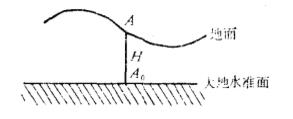
空間改正是將海拔高程為H的重力點上的重力觀測值g歸算成大地水準面上A0點的重力值g0，歸算時不去考慮地面和大地水準面之間的質量，只考慮高度對重力的改正，如下圖：
空間改正的推導
為了簡便起見，在推導改正值時，可以把大地水準面看成是半徑為R的不旋轉的均質圓球，即在重力中不顧及離心力。由於空間改正值很小，這樣假設對結果不會產生什麼影響。
假設在下圖中，A為地面上一點，A0為大地水準面上相應的投影點，A點的高程為H，我們要將A點的重力加以改正歸算到大地水準面上，求出A0點的重力值。現求其改正數。
我們知道，均質圓球是對稱於球心的，故其重心就在球心O上，均質圓球的引力為：
對於地麵點A：
；
對於大地水準面A0點：
；
這裡我們只顧及改正數的絕對值，暫不顧及其符號，將上兩式相減可求得由地面A點歸算到大地水準面上A0點的重力改正值為：
上式右邊
亦可用正常重力γ0來表示，而在方括弧內，因為R是地球的平均半徑，近似地等於6371公里，H是重力點的高程，最高不會超過9公里，所以
是一個微小量，我們可以把上式中的
展成級數，並取至二次項，得
這就是將地面重力值歸算到大地水準面上應加的改正值，稱為空間改正。將地球的平均重力值γ和地球的平均半徑R代入上式，最後求得：
式中高程H以米為單位，Δ1g以毫伽為單位。顯然高程愈高，重力值就愈小，當高程相差3米，空間改正約為1毫伽。第二項在一般情況下可以不必考慮，但在高程特別大的地區（）例如珠穆朗瑪峰地區）必須顧及，因此通常可以將上式寫成：
自由空間改正
經過地形改正和中間層改正後，重力測點仍然位於距離總基點垂直高度為△h的空間。為了消除測點距離地心遠近的影響而進行的改正，稱為“高度改正”或“重力高度改正”。地球正常重力場隨高度變化的改正，常用的近似改正公式為Δg高=0.308Ah(毫伽)。式中△h為測點與總基點的高程差，單位為米。測點高於總基點時，△h取正值；反之，取負值。
如果重力的測定是在船上進行的，並且船是在大地水準面上（平均海平面）航行，那么就不需要作自由空間改正。實際上由於受氣壓或海流等影響，海面與大地水準面是不同的，但其變化不大，從現在海上測定的精度來看，不考慮這項改正也沒關係。
