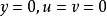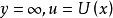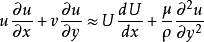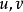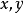流體在大雷諾數下作繞流流動時，在離固體壁面較遠處，粘性力比慣性力小得多，可以忽略；但在固體壁面附近的薄層中，粘性力的影響則不能忽略，沿壁面法線方向存在相當大的速度梯度，這一薄層叫做邊界層。流體的雷諾數越大，邊界層越薄。從邊界層內的流動過渡到外部流動是漸變的，所以邊界層的厚度δ通常定義為從物面到約等於99%的外部流動速度處的垂直距離，它隨著離物體前緣的距離增加而增大。根據雷諾數的大小，邊界層內的流動有層流與湍流兩種形態。一般上游為層流邊界層，下游從某處以後轉變為湍流，且邊界層急劇增厚。層流和湍流之間有一過渡區。當所繞流的物體被加熱（或冷卻）或高速氣流掠過物體時，在鄰近物面的薄層區域有很大的溫度梯度，這一薄層稱為熱邊界層。
基本介紹
- 中文名：邊界層理論
- 外文名：boundary layer theory
- 拼音：biān jiè céng lǐ lùn
- 提出者：路德維希·普朗特
- 時間：1904年
理論提出,基本特徵,分析方法,邊界層方程組,分離和轉捩,分離,轉捩,歷史和發展,背景,提出,發展,
理論提出
邊界層的概念是1904年德國著名的力學家普朗特在海德爾堡第三屆國際數學家學會上宣讀的“關於摩擦極小的流體運動”的論文中首先提出的。他根據理論研究和實際觀察，證實了對於水和空氣等粘性係數很小的流體，在大雷諾數下繞物體流動時，粘性對流動的影響僅限於緊貼物體壁面的薄層中，而在這一薄層外粘性的影響很小，完全可以忽略不計。普朗特把這薄層稱為邊界層，或稱附面層。
右圖所示大雷諾數下粘性流體繞流翼型的二維流動，在極狹窄的邊界層內流體的速度由壁面上的零值急劇地增加到與來流速度同量級的數值，於是在壁面法線方向上的速度梯度很大，即使流體的動力粘性係數很小，但粘性力仍然可達到很大的數值，所以在邊界層內的粘性力和慣性力具有同一數量級。由於速度梯度很大，流體內有相當大的旋渦強度，所以邊界層內是有旋流動。當邊界層內的有旋流動與壁面分離時，在物體後形成一個速度梯度仍較顯著的尾跡區域，由於粘性影響，尾跡中旋渦逐漸擴散，旋渦的動能逐漸變成熱能而耗散掉。
在邊界層和尾跡流以外的區域內，速度梯度很小，因此粘性力比慣性力要小得多，可以忽略不計，而且流動基本上是無旋的，所以可看作是無旋勢流。由此可見，在大雷諾數情況下，粘性流體繞物體流動的流場可劃分為兩個區域：在邊界層和尾跡區內的粘性流休有旋流動區域和在邊界層和尾跡區外的理想流體無旋勢流區域。由於邊界層內的流動是漸近地趨於外部主流，所以邊界層內外區域的分界線是不明顯的，具有一定的任愈性。一般規定與外部勢流速度相差1%處作為邊界層的外邊界，即離壁面達到外勢流速度的99%處的垂直距離，定義為邊界層的厚度。但要注意的是，邊界層的外邊界並不是流線，流線是伸入邊界層內，與外邊界相交的。由實際測量可知，實際上邊界層很薄，以機翼為例，通常邊界層厚度僅為弦長的幾百分之一，可見邊界層的厚度大大小於物體的特徵長度。
定義的邊界層厚度並不是確切的物理量，在實際套用時，可能會由於速度的測量或計算誤差的不同而使數值有較大的差異。所以在工程上常採用以下三種與邊界層內速度分布有關的、並具有一定物理意義的邊界層厚度，它們分別為位移厚度、動量損失厚度和能量損失厚度。
邊界層厚度
邊界層厚度基本特徵
⑴ 與物體的特徵長度相比，邊界層的厚度很小。
⑵ 邊界層內沿厚度方向，存在很大的速度梯度。
⑶ 邊界層厚度沿流體流動方向是增加的，由於邊界層內流體質點受到粘性力的作用，流動速度降低，所以要達到外部勢流速度，邊界層厚度必然逐漸增加。
⑷ 山於邊界層很薄，可以近似認為邊界層中各截面上的壓強等於同一截面上邊界層外邊界上的壓強值。
⑸ 在邊界層內，粘性力與慣性力同一數量級。
分析方法
大雷諾數的繞流流動可分為兩個區，即很薄的一層邊界層區和邊界層以外的無粘性流動區。因此，處理粘性流體的方法是：略去粘性和熱傳導，把流場計算出來，然後用這樣的初次近似求得的物體表面上的壓力、速度和溫度分布作為邊界層外邊界條件去解這一物體的邊界層問題。算出邊界層就可算出物面上的阻力和傳熱量。如此的疊代程式使問題求解大為簡化，這就是經典的普朗特邊界層理論的基本方法。
邊界層方程組
不可壓縮流體在大雷諾數的層流情況下繞過平滑壁面的情況（見圖）。在此考慮二維定常不可壓縮流動。規定沿物體壁面的方向為x軸，垂直於壁面的方向為y軸。由於邊界層厚度δ比物面特徵尺寸L小得多，因此對二維的忽略重力的納維－斯托克斯方程逐項進行數量級分析，在忽略數量級小的各項後，可近似認為邊界層垂直方向的壓力不變，從而得到層流邊界層方程組為：
方程組邊界條件
分離和轉捩
分離
邊界層脫離物面並在物面附近出現回流的現象。當邊界層外流壓力沿流動方向增加得足夠快時，與流動方向相反的壓差作用力和壁面粘性阻力使邊界層內流體的動量減少，從而在物面某處開始產生分離，形成回流區或漩渦，導致很大的能量耗散。繞流過圓柱、圓球等鈍頭物體後的流動，角度大的錐形擴散管內的流動是這種分離的典型例子。分離區沿物面的壓力分布與按無粘性流體計算的結果有很大出入，常由實驗決定。邊界層分離區域大的繞流物體，由於物面壓力發生大的變化，物體前後壓力明顯不平衡，一般存在著比粘性摩擦阻力大得多的壓差阻力（又稱形阻）。當層流邊界層在到達分離點前已轉變為湍流時，由於湍流的強烈混合效應，分離點會後移。這樣，雖然增大了摩擦阻力，但壓差阻力大為降低，從而減少能量損失。
在定常流動中，邊界層分離是逆壓梯度和壁面粘性力阻滯的綜合作用的結果。粘性流體在順壓梯度區域內流動時，決不會發生邊界層分離。只有在逆壓梯度區域內，當逆壓梯度有足夠大時才能發生邊界層分離。邊界層分離後，邊界層的厚度大大增加，推導邊界層方程的基本條件已不成立，量級關係也發生了根本變化，所以邊界層理論已不再適用。
層流邊界層和紊流邊界層都能發生分離，但由於紊流內脈動運動引起的動量交換，使邊界層內的速度剖面均勻化，增大壁面附近流體的動能，所以紊流邊界層比層流邊界層承受較大的逆壓梯度，而不易分離。
轉捩
邊界層內的流動狀態，在低雷諾數時是層流，在高雷諾數時是紊流。當粘性流體繞流物體時，在物體前緣附近是層流。隨著離前緣的距離的不斷增加，雷諾數也逐漸加大，層流邊界層流動隨雷諾數增加會出現不穩定現象。流體中不可避免地存在著擾動，使層流發生變化，向紊流過渡，最終完全變成了紊流。層流向紊流的過渡稱為轉捩。
歷史和發展
背景
1755年由歐拉（1707-1783）建立的理想流體的運動方程奠定了流體力學的基礎，後經拉格朗日（1736-1813）、拉普拉斯（1749~1827）等在數學解析方法上進一步的發展和完善，形成了流體力學的一個重要分支——理論流體力學。它是運用嚴密的數學工具研究無粘性的理想流體流動問題，但由於忽略了流體實際存在的粘性作用，所以根據理論流體力學純數學分析得到的理論計算與實際結果不盡相符，甚至差別很大。例如與歐拉同一時期的達朗貝爾（1717-1783）用理論確定物體在理想流休中運動的阻力等於零這個出乎意料的結果，被稱為達朗貝爾疑題。由此可見，在研究阻力問題時。理想流體理論已無能為力。
19世紀中，隨著航海、水利工程等的迅速發展，流體力學的另一個重要分支，研究不可壓縮粘性流體流動的水力學得到很大的發展。它是建立在大量實驗測量的基礎上。當時如哈根、泊肅葉、雷諾等用實驗研究水和其他粘性流體在管道和槽渠中流動時的阻力和壓強損失問題、得到的有關粘性流體的實驗研究成果，有助於解決某些工程實際問題。但由於水力學在理論指導上的不足，由實驗成果得出的經驗公式和半經驗理論公式有一定的局限性。於是在19世紀中葉產生了粘性流體運動的理論，1827年，納維爾在歐拉運動微分方程中加上粘性項，第一個得到粘性流體運動微分方程。1846年，斯托克斯嚴格地導出了這個方程，稱為納維爾-斯托克斯方程，簡稱N-S方程。雖然N-S方程對粘性流體流動問題的研究分析有所幫助，但對這個方程數學上的求解是十分複雜和困難的。1851年，斯托克斯對N-S方程作了某些簡化，略去方程中的慣性項，也就是在非常緩慢的流體流動條件下，計算出球體在流動的粘性流體中所受到的阻力。
提出
到20世紀初，航空工業的發展，需要解決粘性流體中較大速度的物體運動問題，促使粘性流體運動的理論大大地向前推進。1904年普朗特（1875-1953）在德國海德爾堡第三屆國際數學家學會上宣讀題為“關於摩擦極小的流體運動”的論文，建立了邊界層理論。他根據對水槽中水流實驗的觀察分析，提出邊界層的概念：粘性極小的流體繞物體流動時，在緊靠物體附近存在著一層極薄的邊界層，其中粘性起著很大的影響。而在邊界層外，流體中的粘性可以忽略不計，可認為是理想流體。由於邊界層極薄，經簡化N-S方程得出普朗特邊界層方程，對過去不可理解和難以解答的現象，如流體阻力問題，給予明確的解答。普朗特建立的邊界層理論，改變了長期以來理論流體力學和水力學相互脫節的狀況，將理論與實踐緊密地聯繫在一起，形成了理論與實驗並重的現代流體力學。
發展
1907年，布拉修斯成功地套用邊界層理論計算在流體中運動物體的摩擦阻力。1921年，卡門和波耳豪森提出了邊界層動能積分方程，以計算邊界層問題，這個方程經霍爾斯坦-博倫（1940）和瓦茨進行簡化和改進，到現在還被廣泛套用。另外邊界層動能積分方程和熱能積分方程分別由萊本森和弗蘭克爾提出。這三個邊界層的近似計算方法使邊界層理論在工程界中很快地推廣開來。1925年，普朗特提出的混合長度理論和1930年卡門提出的相似性理論，將邊界層理論推廣到紊流邊界層、射流和物體後的尾跡流中去。從層流向紊流的轉捩現象是流體動力學中的基本現象。早在19世紀末，雷諾就首先對轉捩現象進行了研究。1914年，普朗特做了著名的圓球實驗，正確地指出：邊界層中的流動可以是層流的，也可以是紊流的，還指出邊界層分離的問題，因此計算阻力的問題是受這種轉捩支配的。從層流向紊流的轉捩過程的理論研究，是以雷諾的假設為基礎的，即承認紊流是由於層流邊界層產生不穩定性的結果。1921年，普朗特開始進行轉捩的理論研究，1929年獲得成功。當時托爾明從理論上算出零沖角平板轉捩的臨界雷諾數，後被別人所進行非常仔細的實驗所證實。穩定性理論能夠考慮到對轉捩有影響的壓強梯度、抽吸、馬赫數和傳熱等許多因素。這個理論已得到很多重要的套用，如設計阻力非常小的層流翼型。
1904年，普朗特發表邊界層理論，除解決了定常平面邊界層問題外。還解決了最簡單的旋轉軸對稱的空間邊界層問題，而一般的空間三維邊界層問題雖然列維-齊維他在1929年早已提出，但長期以來還是靠實驗方法進行研究。塞爾斯、莫爾、施里希廷、柯克-哈爾相繼發表了關於三維邊界層的綜述文章，柯姆普斯迪-海特研究了三維紊流邊界層的問題，但由於許多三維邊界層流動的圖像和物理特性太複雜，長期以來難以進行數值處理。目前所有的三維邊界層的理論方法距離實際套用還很遠。
在20世紀的初期和中期，隨著航空用渦輪機械製造以及現代的火箭和人造衛星噴氣推進技術發展，可壓縮流動中的邊界層理論也得到了迅速的發展。在可壓縮流邊界層中除速度邊界層外，還有溫度邊界層。1910年，普朗特把邊界層的概念套用於熱傳遞，1921年，波耳豪森首先求得平板層流溫度邊界層的近似解，後來奧斯特勒克作出更精確的計算。由於可壓縮流邊界層方程組是非線性偏微分方程，求解仍很困難。密塞斯、卡門-錢學森、克羅柯等設法通過坐標變換，把可壓縮層流邊界層方程變換成為與不可壓縮層流邊界層相近似的形式，以後伊林沃思、霍華斯和史土瓦遜作了某些改進，致使可壓縮層流邊界層問題較易進行數值計算。而對於可壓縮紊流邊界層的研究還限制在普朗特混合長度理論等的半經驗理論基礎上，並對壓縮性的影響作某些假設，德律斯特首先在這方面作了研究。以上這些研究作對可壓縮邊界層理論的進一步發展起了很大的推動作用。
