基本介紹
定義
定義方式
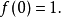
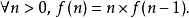
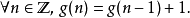
構成
舉例
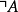
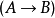
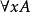
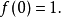
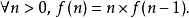
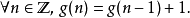
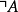
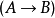
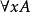
遞歸定義是數理邏輯和計算機科學用到的一種定義方式,使用被定義對象的自身來為其下定義(簡單說就是自我複製的定義)。遞歸定義(recursive definition)亦稱歸納定義,一...
程式調用自身的編程技巧稱為遞歸( recursion)。遞歸做為一種算法在程式設計語言中廣泛套用。 一個過程或函式在其定義或說明中有直接或間接調用自身的一種方法,它...
遞歸算法(英語:recursion algorithm)在計算機科學中是指一種通過重複將問題分解為同類的子問題而解決問題的方法。遞歸式方法可以被用於解決很多的計算機科學問題,因此它...
程式語言中,函式Func(Type a,……)直接或間接調用函式本身,則該函式稱為遞歸函式。遞歸函式不能定義為內聯函式。在數學上,關於遞歸函式的定義如下:對於某一函式...
遞歸法是設計和描述算法的一種有力的工具,由於它在複雜算法的描述中被經常採用,為此在進一步介紹其他算法設計方法之前先討論它。...
設(a0,a1,...,ar,...)是一個序列,把該序列中的ar和它前面的幾個ai(0≤i<r)關聯起來的方程稱做一個遞歸關係。如關係式:ar=3ar-1 (r≥1)和錯排數...
在計算機程式語言,一個遞歸類型(也被稱為遞歸定義,電感定義或感應數據類型)是一種數據類型,選擇那些包含相同類型的其它值的值。遞歸類型的數據通常被視為有向圖。...
所謂遞歸 ,籠統地說 ,是指運用收集到的知識作為行動的基礎去獲得更多的知識。由於這裡所涉及的往往是多個、甚至是無窮多個未知量 ,因此 ,所謂的遞歸事實上也就...
一個直接調用自己或通過一系列的過程語句間接地調用自己的過程,稱做遞歸過程。棧的另一個重要套用是在程式設計語言中實現遞歸過程,遞歸是程式設計中一個強有力的...
遞歸調用是一種特殊的嵌套調用,是某個函式調用自己或者是調用其他函式後再次調用自己的,只要函式之間互相調用能產生循環的則一定是遞歸調用,遞歸調用一種解決方案,一...
當遞推式中只含數列中的項,而無常數項或其它項時,就叫做遞歸公式。遞歸程式設計的公式化方法是一種簡單而有效的設計思想,它把程式設計和程式理解的難點都集中到...
問題如下。我們需要給予程式如階乘函式的定義以語義function factorial(n:Nat):Nat ≡ if (n==0)then 1 else n*factorial(n-1)。 這個階乘程式的意義應當是...
遞歸性(recursiveness),也可相近地理解為層次性或有機性。是機體或系統的共性,是系統得以存在,運作和發展的基本手段。遞歸性不僅是轉換生成語法中的一種語法屬性,...
遞歸做為一種算法在程式設計語言中廣泛套用。是指函式/過程/子程式在運行過程中直接或間接調用自身而產生的重入現象。遞歸是計算機科學的一個重要概念,遞歸的方法是...
在數學、邏輯和計算機科學中,遞歸語言或遞迴語言是也叫做可判定語言或圖靈可判定語言的形式語言類型。所有遞歸語言的類經常被稱為 R。這種語言類型在喬姆斯基層級中...
一種計算過程,如果其中每一步都要用到前一步或前幾步的結果,稱為遞歸的。用遞歸過程定義的函式,稱為遞歸函式,例如連加、連乘及階乘等。凡是遞歸的函式,都是可...
共遞歸在計算機科學重視一類操作,與遞歸在範疇論上對偶。...... 共遞歸定義 編輯 共遞歸在計算機科學重視一類操作,與遞歸在範疇論上對偶。因而遞歸是分析地工作,把...
遞歸方法,是降格策略反映到數學思維中的一種方法,指從初始條件出發,利用遞推關係而求得一般結果的方法,例如降維法。...
遞歸定理(recursion theorem)亦稱不動點定理。反映部分遞歸函式類基本性質的重要定理。最初是由美國邏輯學家、數學家克林(Kleene, S. C.)於1938年證明的,克林所...
遞歸指的是,一個函式不斷引用自身,直到引用的唯一已知對象時止的過程。...... 遞歸指的是,一個函式不斷引用自身,直到引用的唯一已知對象時止的過程。...
遞歸數列 (recursive sequence ):一種給定A1後,用給定遞歸公式An+1=f(An)由前項定義後項所得到的數列。...
遞歸查詢是最常見的查詢方式,域名伺服器將代替提出請求的客戶機(下級DNS伺服器)進行域名查詢,若域名伺服器不能直接回答,則域名伺服器會在域各樹中的各分支的上下...
遞歸論(Recursion theory)是數理邏輯的重要分支之一,研究解決問題的可行的計算方法和計算的複雜程度的一門學科,尤其是研究遞歸函式及其推廣。遞歸論研究的函式主要包括...
