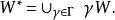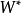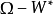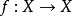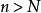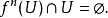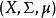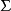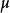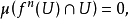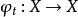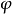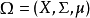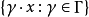遊蕩集

在動力系統及遍歷理論等數學的分支里，遊蕩集此一概念公式化了此系統中運動和混合的某些概念。當一個動力系統存在一非零測度的遊蕩集時，即代表此系統為一耗散結構。這和使用始態復現定理概念的保守系統極為不同。直覺上，遊蕩集和耗散結構之間的關係是很容易了解的：若一部分相空間在此系統正常的時間演化下會“遊蕩開來”，且不再接近，則此系統即是耗散的。使用遊蕩集的語言可以使耗散結構的概念有一個精確、數學的定義。

基本介紹

• 中文名：遊蕩集
• 外文名：Wandering set
• 分類：遍歷理論
• 領域：數理科學

遊蕩點

遊蕩集的一普通且離散時間的定義開始於一拓撲空間X本身的映射。X內的x被稱為遊蕩點若存在一x的鄰域U及一正整數N使得對所有的，其和其疊代函式都不會相交：

另有一個較方便的定義，只需要其交集為零測度即可。更精確地說，此一定義需要X為一測度空間，即部分的三元組，其中為博雷爾集合，測度會使得

類似地，一連續時間的系統有一映射，其定義了此系統的時間演化或稱為此系統的流量，其中時間演化算符為一於X上的一元連續阿貝爾群作用：

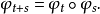
在此情況下，一個於X內的遊蕩點x會有一個x的鄰域U及一時間T，使得對所有時間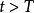，其時間演化映射為零測度：

此一較簡單的定義可以完全地被廣義化至一般的群作用上。設為一測度空間，即一具有定義於其博雷爾集合上之測度的集合。再設Γ為作用在此集合上的群。給定一於Ω內的點x，此集合稱做點x的軌跡或軌道。

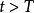
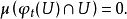
於Ω內的一元素x被稱為一遊蕩點，若存在一x的鄰域U及Γ單位元的鄰域V，使得對所有的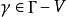

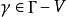
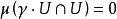
非遊蕩點

非遊蕩點的定義在感覺上剛好相反。在離散的例子裡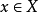，為非遊蕩點，若對每一包含x的開集合U，都可以找到在一些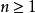中，

相類的定義也可以被使用在連續時間及離散與連續群作用里。

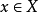
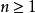
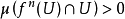
遊蕩集和耗散系統

一個遊蕩集為遊蕩點的聚合。更精確地說，Ω的子集W為一在一離散群Γ的群作用下的遊蕩集，若W為可測度的且對任一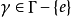，交集

為一零測度的集點。

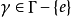
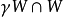
遊蕩集的概念在感覺上是和始態復現定理內所表示出來的概念互為正反。若存在一正測度的遊蕩集，Γ的群作用便被稱為耗散的，且此一動力系統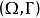則被稱為耗散結構。若不存在如此的遊蕩集，此一群作用則被稱為保守的，且此一系統稱為保守系統。例如，任何遵守始態復現定理的系統在定義上不可能存在正測度的遊蕩集；且因此為保守系統的例子。

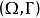
一遊蕩集W軌跡的定義為

Γ的作用稱為完全耗散的，若存在一正測度的遊蕩集W，使得軌道幾乎處處相等於Ω，即若

為一零測度的集合。