通徑(latus rectum) 亦稱“正通徑”、“首通徑”、“直焦弦”、“主焦弦”、“正焦弦”。過圓錐曲線的焦點且與過焦點的軸垂直的弦稱為通徑,清代明安圖《割環密率捷法》中,稱圓的直徑為通徑。
基本介紹
- 中文名:通徑
- 外文名:latus rectum
- 屬性:圓錐曲線的參數
- 別稱:正通徑、直焦弦、正焦弦等
橢圓的通徑
定義
 圖1
圖1橢圓的參數方程與離心率


橢圓的焦準距

拋物線的通徑
 圖2
圖2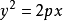






雙曲線的通徑






 圖3
圖3
通徑(latus rectum) 亦稱“正通徑”、“首通徑”、“直焦弦”、“主焦弦”、“正焦弦”。過圓錐曲線的焦點且與過焦點的軸垂直的弦稱為通徑,清代明安圖《割環密率捷法》中,稱圓的直徑為通徑。
 圖1
圖1


 圖2
圖2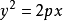












 圖3
圖3通徑(latus rectum) 亦稱“正通徑”、“首通徑”、“直焦弦”、“主焦弦”、“正焦弦”。過圓錐曲線的焦點且與過焦點的軸垂直的弦稱為通徑,清代明安圖《割...
公稱通徑是管路系統中所有管路附屬檔案用數字表示的尺寸,公稱通徑是供參考用的一個方便的圓整數,與加工尺寸僅呈不嚴格的關係。公稱通徑用字母“DN”後面緊跟一個數字...
通徑分析(path analysis)可用於分析多個自變數與因變數之間的線性關係,是回歸分析的拓展,可以處理較為複雜的變數關係。...
橢圓通徑長定理,指的是橢圓的通徑AB就是過焦點垂直於長軸的直線與橢圓相交所得的線段AB。可以由勾股定理推導。橢圓中的通徑是通過焦點最短的弦。...
通徑規,井下作業常用的檢測工具,套管通徑規和油管、鑽桿通徑規。...... 主要用於檢測套管、油管、鑽桿等內孔的通徑尺寸是否符合標準,是井下作業常用的檢測工具。 [...
結構套管通徑規由接頭與本體兩部分組成。上下兩端均加工有連線螺紋,上端與鑽具相連線,下端備用。操作方法(1)將套管通徑規連線在下井管柱下入井內,通徑規應能順利...
特殊連線埠和通徑抗靜電裝置閥桿能緊急處理油脂閥座潤滑劑和緊急密封劑設備金屬對金屬閥座密封雙切斷和排放雙活塞作用閥座帶有石墨墊圈的安全防火設計...
通徑收縮即如果一個閥體內的通道直徑不一樣,往往都是閥座處的通徑小於法蘭連線處的通徑。...
中通徑閥門:公稱通徑DN為50~300mm的閥門。 ...... 中通徑閥門:公稱通徑DN為50~300mm的閥門。V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最...
特大通徑閥門:公稱通徑DN≥1400mm的閥門。 ...... 特大通徑閥門:公稱通徑DN≥1400mm的閥門。詞條標籤: 科技產品 , 科學 V百科往期回顧 詞條統計 瀏覽次數:次 ...
通徑係數編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!中文名稱 通徑係數 英文名稱 path coefficient 定義 表示...
大通徑閥門:公稱閥門DN為350~1200mm的閥門。 ...... 大通徑閥門 大通徑閥門:公稱閥門DN為350~1200mm的閥門。詞條標籤: 科技產品 , 科學 V百科往期回顧 詞條...
圖集 朱光潛-從迷途到通徑圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:5次歷史版本 最近更新: 創建者:杏仁茶丶392猜你喜歡...
ZCZP大通徑電磁閥編輯 鎖定 本閥是有副閥和主閥兩大部件構成的先導式二次開闊的電磁閥。是 靠副閥的啟閉來控制主閥的通斷。根據斷電時所處開關狀態的不同,...
大通徑電磁閥用於各種常溫、高溫、常壓、高壓場合,適用於自來水、熱水、超淨流體、腐蝕性流體、尤其是過熱蒸汽、飽和蒸汽及導熱油管路的自動控制。...
公稱通徑是管路系統中所有管路附屬檔案用數字表示的尺寸,公稱通徑是供參考用的一個方便的圓整數,與加工尺寸僅呈不嚴格的關係。公稱通徑用字母“DN”後面緊跟一個數字...
