定義
第二宇宙速度--當物體(太空飛行器)飛行速度達到11.2千米/秒時,就可以擺脫地球引力的束縛,飛離地球進入環繞太陽運行的軌道,不再繞地球運行。這個脫離地球引力的最小速度就是第二宇宙速度。各種行星或衛星探測器的起始飛行速度都高於第二宇宙速度。
第二宇宙速度v當太空飛行器超過第一宇宙速度v達到一定值時,它就會脫離地球的引力場而成為圍繞太陽運行的人造行星,這個速度就叫做第二宇宙速度,亦稱逃逸速度。按照力學理論可以計算出第二宇宙速度v=11.2km/s。
第二宇宙速度即逃逸速度,一物體的
動能等於該物體的
重力勢能的大小時的該物體的
速率。逃逸速度一般描述為擺脫一
重力場的引力束縛飛離那重力場所需的最低速率。
決定因素
逃逸速度取決與星球的質量。如果一個星球的質量大,其引力就強,逃逸速度值就高。反之一個較輕的星球將會有較小的逃逸速度。逃逸速度還取決於物體與星球中心的距離。距離越近,逃逸速度越大。地球的逃逸速度是11.2公里/秒,太陽的逃逸速度為617.7公里/秒。如果一個天體的質量與表面引力很大,使得逃逸速度達到甚至超過了光速,該天體就是
黑洞。黑洞的逃逸速度達30萬千米/秒。一般認為宇宙沒有邊界,說宇宙中的物質逃離到別的地方去這樣的問題沒有意義,因此,說宇宙的逃逸速度也似乎沒有意義。
 逃逸速度
逃逸速度不過,宇宙正在膨脹,即星系都在向遠處運動(相互遠離),這就存在這樣一個問題:如果宇宙的膨脹速度足夠大,星系就會克服宇宙的總引力而永遠膨脹下去。這就好像星系在逃離一樣。這裡,膨脹速度也就等同逃離速度了。當然,如果膨脹速度不夠大,膨脹終將停止,宇宙的總引力將會使星系相互靠近,就像飛離地球的物體再掉回來一樣。
因此,這樣來理解宇宙的逃逸速度,就成了一個很有意義的問題。宇宙是永遠膨脹還是轉而收縮,取決於膨脹速度和總引力的大小。由於膨脹速度可以測定,因而就取決於宇宙的總引力,實際上就是宇宙到底有多重。
從物理學界的普遍看法來講,宇宙源於一個奇點——也就是黑洞。而黑洞則是連
光速運動的物體也無法逃脫的。光速是連續運動的速度極限,任何作連續運動的物體都無法超越光速。所以,宇宙是不存在逃逸速度的。
某星體的逃逸速度是逃脫該星體引力束縛的最低速度。
 衛星的發射速度
衛星的發射速度具有逃逸速度並不代表可以逃脫引力範圍(因為引力範圍無限)。逃逸速度只是數學上的一個計算極限。
逃脫引力束縛並不代表不受引力,它只代表物體不會再因為引力而無法到達更遠的地方。引力是一個長程單向力,無論距離引力源多遠,引力都不會消失。只是因為在距引力源足夠遠時,引力影響變得極弱,足以忽略不計。所以說,引力並沒有所謂的範圍,它無時無刻都在。
綜上,逃逸速度的計算與距引力源的距離無關,只與引力源的質量大小有關。
計算方法
一個質量為m的物體具有速度v,則它具有的動能為mv^2/2。假設無窮遠地方的
引力勢能為零(應為物體距離地球無窮遠時,物體受到的引力勢能為零,所以這個假設是合理的),則距離地球距離為r的物體的勢能為-mar(a為該點物體的
重力加速度,負號表示物體的勢能比無窮遠點的勢能小)。又因為地球對物體的引力可視為物體的重量,所以有
GmM/r2=ma
即a=(GM)/r2.
所以物體的勢能又可寫為-GmM/r,其中M為
地球質量。設物體在地面的速度為V,
地球半徑為R,則根據
能量守恆定律可知,在地球表面物體動能與
勢能之和等於在r處的動能與勢能之和,即
mV2/2+(-GMm/R)=mv2/2+(-GmM/r)。
當物體擺脫地球引力時,r可看作無窮大,引力勢能為零,則上式變為
mV2/2-GmM/R=mv2/2.
顯然,當v等於零時,所需的
脫離速度V最小,即V=2GM/R開根號,
 逃逸速度
逃逸速度又因為
GMm/R2=mg,
所以
V=2gR開根號,
其中g為地球表面的重力加速度,其值為9.8
牛頓/千克。地球半徑R約為6370千米,從而最終得到地球的脫離速度為11.17千米/秒。
不同天體有不同的逃逸速度,脫離速度公式也同樣適用於其他天體。
宇宙速度分類
第一宇宙速度
人類的航天活動,並不是一味地要逃離地球。特別是當前的套用太空飛行器,需要繞地球飛行,即讓太空飛行器作
圓周運動。要作圓周運動,必須始終有一個力作用在太空飛行器上。其大小等於該太空飛行器運行
線速度的平方乘以其質量再除以公轉半徑,即F=mv
2/R,其中v
2/R是物體作圓周運動的
向心加速度。在這裡,正好可以利用地球的引力,在合適的軌道半徑和速度下,地球對物體的引力,正好等於物體作圓周運動的
向心力。第一宇宙速度又稱
環繞速度。實際上,地球表面存在稠密的
大氣層,太空飛行器不可能貼近地球表面作圓周運動,必需在150千米的飛行高度上,才能繞地球作圓周運動。在此高度下的環繞速度為7.9千米/秒。
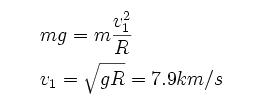 第一宇宙速度
第一宇宙速度 第一宇宙速度
第一宇宙速度第二宇宙速度
第二宇宙速度又稱為逃逸速度,指物體完全擺脫地球引力束縛,飛離地球的所需要的最小初始速度。同樣,由於地球表面稠密的大氣層,太空飛行器難以這樣高的初始速度起飛,實際上,太空飛行器是先離開大氣層,再加速完成脫離的(例如先抵達近地軌道,再在該軌道加速)。在這高度下,太空飛行器的脫離速度較小,約為11.2千米/秒。
第三宇宙速度
第三宇宙速度又稱為脫離速度,是指在地球上發射的物體擺脫太陽引力束縛,飛出太陽系所需的最小初始速度,約為16.7km/s。本來,在
地球軌道上,要脫離太陽引力所需的初始速度為42.1千米/秒,但
地球繞太陽公轉時令地面所有物體已具有29.8千米/秒的初始速度,故此若沿地球公轉方向
發射,只需在脫離
地球引力以外額外再加上12.3千米/秒的速度,本來逃逸速度是一個無方向概念,但第三宇宙速度由於要藉助地球公轉的初始速度,所以額外疊加的12.3千米/秒的速度方向應與地球公轉速度方向相同。
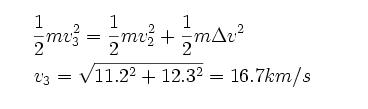 第三宇宙速度
第三宇宙速度第四宇宙速度
第四宇宙速度是指在地球上發射的物體擺脫銀河系引力束縛,飛出銀河系所需的最小初始速度。但由於人們尚未知道銀河系的準確大小與質量,因此只能粗略估算,其數值在110~120千米/秒之間。而實際上,仍然沒有太空飛行器能夠達到這個速度。
宇宙速度的概念也可套用於在其他天體發射太空飛行器的情況。例如計算火星的環繞速度和逃逸速度,只需要把公式中的M、R、g換成火星的質量、半徑、表面重力加速度即可。
研究意義
逃逸速度,取決於星球的質量。如果一個星球的質量大,其引力就強,逃逸速度值就大。反之,一個較輕的星球,將會有較小的逃逸速度。逃逸速度還取決於物體與星球中心的距離,距離越近,逃逸速度越大。如果一個天體的質量與表面引力很大,使得逃逸速度達到甚至超過了光速,該天體就是黑洞。黑洞的逃逸速度達30萬千米/秒。一般認為,宇宙沒有邊界,說宇宙中的物質逃離到別的地方去這樣的問題是沒有意義的。因此,討論宇宙的逃逸速度,也似乎沒有意義。
不過,宇宙正在膨脹,即星系都在向遠處運動(相互遠離),這就存在這樣一個問題:如果宇宙的膨脹速度足夠大,星系就會克服宇宙的總引力,而永遠膨脹下去,這就好像星系在逃離一樣。這裡,膨脹速度也就等同逃離速度。當然,如果膨脹速度不夠大,膨脹終將停止,宇宙的總引力將會使星系相互靠近,就像飛離地球的物體再掉回來一樣。
因此,這樣來理解宇宙的逃逸速度,就成了一個很有意義的問題。宇宙是永遠膨脹還是轉而收縮,取決於膨脹速度和總引力的大小。由於膨脹速度可以測定,因而就取決於宇宙的總引力,實際上就是宇宙到底有多重。
逃逸速度是一個質點永遠脫離母體引力必須具有最小速度,如果僅從質點具有大於逃逸速度後脫離母體引力作用遠去他處,這樣理解是不全面的,逃逸速度還有深遠意義,本文將討論逃逸速度就是母體引力作用傳遞速度。
 逃逸速度
逃逸速度 衛星的發射速度
衛星的發射速度 逃逸速度
逃逸速度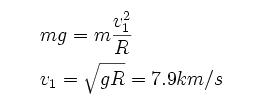 第一宇宙速度
第一宇宙速度 第一宇宙速度
第一宇宙速度
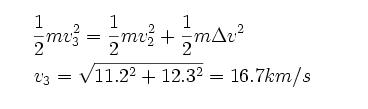 第三宇宙速度
第三宇宙速度