重力勢能(gravitational potential energy)是物體因為重力作用而擁有的能量，對於重力勢能，其大小由地球和地面上物體的相對位置決定。物體的質量越大、相對的位置越高、做的功越多，從而使物體具有的重力勢能變大，它的表達式為：Ep=mgh。
基本介紹
基本含義,決定因素,公式,特點,勢能,定義,類別,性質,
基本含義
勢能：勢能是相互作用的物體憑藉其相對位置而具有的能量。
物體由於被舉高而具有的能叫做重力勢能(gravitational potential energy)。是在特殊情形下引力勢能的推廣，是物體在重力的作用下而具有由空間位置決定的能量，大小與確定其空間位置所選取的參考點有關。物體在空間某點處的重力勢能等於使物體從該點運動到參考點（即一特定水平面）時重力所作的功。
決定因素
物體重力勢能的大小由地球對物體的引力大小以及地球和地面上物體的相對位置決定。物體質量越大、位置越高、做功本領越大，物體具有的重力勢能就越多。
某種程度上來說，就是當高度一定時，質量越大，重力勢能越大；質量一定時，高度越高，重力勢能越大
公式
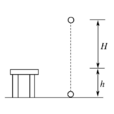
重力勢能的公式：Ep=mgh （Ep為重力勢能，m為質量，g為地球表面重力加速度，在大多數情況下，h為物體距離參考平面的高度）
由於萬有引力和g都因距離而變化，所以Ep=mgh只能解決地球表面問題。
以無窮遠處為0勢能，重力勢能的一般形式為：
可用定積分計算萬有引力的變力作功求解
假設一個物體從離地心r1的距離被提升到了r2的距離，即r2大於r1
這時重力做功大小為
其中Fr代表物體所受的向心重力，
由於物體遠離地心移動，重力做負功，故需要添加負號
又由於物體所受重力由定義式得：
故
於是我們得到重力勢能的定義式
其中r為物體離地球中心的距離。
關於負號的理解：當物體被從無限遠處由重力做功移向施力體中心的時候，重力做功，勢能減小。
判斷一個物體是否具有重力勢能，關鍵看此物體相對某一個平面有沒有被舉高，即相對此平面有沒有一定的高度。若有，則物體具有重力勢能，若沒有，則物體不具備重力勢能。
物理學中，物體具有的重力勢能的大小與物體的質量成正比，與物體被舉高的高度成正比。所以得出：
Ep=mgh。重力勢能是標量，單位為焦耳(J)。與功不同的是,功的正負號表示作用效果,比較大小時僅比較數值;而重力勢能中正數一律大於負數.在重力勢能的表達式中，由於高度h是相對的，因此重力勢能的數值也是相對的。我們說某個物體具有重力勢能mgh，這是相對於某一個水平面來說的，若把這個水平面的高度取做零，這個水平面稱為參考平面，物體位於這個參考平面上時，重力勢能為零，因此參考平面也被稱為零勢能平面。經典物理對重力勢能的理解就是當一個物體處在一個位置,相對於參照平面,重力可以對物體做多少功,使物體獲得多少其他形式的能量,就說重力勢能是多少。但並不是說重力勢能為0就不具備做功的能力,這是由其相對性決定的。重力做正功時，重力勢能減小，重力做負功時，重力勢能增大。兩個物體僅受萬有引力而相互吸引的重力勢能：
兩個物體僅受萬有引力而相互吸引的過程其實很複雜，首先要把二體問題（兩個物體之間由於引力運動的問題）轉化為單體問題（一個物體受到另一個固定的物體的引力而運動的問題，轉化的方法在某些普通物理教材和理論物理力學教材當中有講），再把直線運動的過程看成是橢圓運動過程的極限，根據克卜勒第三定律求解。另外，如果求的是碰撞前的瞬時速度的話，可以先用動量守恆判斷出碰撞前兩個物體的速度之比，再用機械能守恆求出碰撞時的速度，不過這種方法要求碰撞的物體是有大小的球體，否則只把它們看作質點的話碰前一剎那的引力勢能為負無窮大。
如果考慮g是變數的話，那么重力勢能就過渡到引力勢能，引力勢能表達式是-GMm/r，不過零勢能處在無窮遠。
物體由於做機械運動所具有的能量，叫機械能。包括動能和勢能兩種，勢能又包括重力勢能和彈性勢能，由於重力和萬有引力是同性質的力，因此在物體的高度不能忽略時，將重力勢能稱作引力勢能更合適些，也就是說，重力勢能就是引力勢能，考綱中，除專門討論重力隨物體在地球上的位置（緯度和高度）變化而變化外，認為重力等於萬有引力，因此也可以認為物體的重力勢能等於引力勢能。*為下標。
重力勢能-GMm/r的相對性與重力勢能變化的絕對性
特點
重力做功與路徑無關，只與起點和終點的位置有關
重力勢能與重力做功
重力做正功，重力勢能減少；重力做負功，重力勢能增加；可理解為重力做功等於重力勢能變化量的負值，即：
。
比較項目 | 重力做功 | 重力勢能 |
物理意義 | 重力對物體所做的功 | 由於物體與地球的相互作用，且由它們之間的相對位置決定的能 |
表達式 |  | Ep=mgh |
影響大小的因素 | 重力G和初、末位置的高度差△h | 重力mg和某一位置的高度h |
特點 | 只與初、末位置的高度差有關，與 路徑及參考平面的選擇無關 | 與參考平面的選擇有關，同一位置的物體 |
過程量 | 狀態量 |
勢能
定義
人們在打樁時，先把重錘高高舉起，重錘落下就能把木樁打入地里。重錘是由於被舉高而能夠做功的，舉高的物體具有的能量叫重力勢能。物體的質量越大，舉得越高，它具有的重力勢能就越大。被舉高的重錘具有重力勢能。重錘的質量越大，被舉得越高，下落時做的功越多，表示重錘的重力勢能越大。（不是所有的舉高都是人為的，而是相對水平面上升的高度為被舉高的高度）
射箭運動員把弓拉彎，放手後被拉彎的弓能把箭射出去．被壓縮的彈簧在放鬆後能把壓在上面的砝碼舉起．弓和彈簧都是由於發生彈性形變而能夠做功的，發生彈性形變的物體具有的能量叫彈性勢能．物體的彈性形變越大，它具有的彈性勢能就越大．
類別
勢能分為重力勢能、彈性勢能、分子勢能、電勢能、引力勢能等。勢能是無限能源。
[重力勢能](Gravitational Potential Energy)是物體因為重力作用而擁有的能量，公式為Ep=mgh （m為質量，g應取9.8N/kg（大多數情況下），h物體距水平面的高度）
實際上，勢能Ep與力F、距離h(彈性勢能為x，引力勢能為r等)存在著一定的關係，既是d(Ep)/dh=F。也可以寫成Ep=∫Fdh，既是保守力所做的功的大小。
性質
勢能是一個標量函式，當一個物體與多個物體共有勢能或共有多種勢能時，這個物體所具有的總勢能為所有勢能的代數和。
由定義可知，勢能取決於兩個或多個物體的相對位形，是兩個或多個物體所共有的。然而，在兩物體A、B組成的保守體系中，如果我們以其中一個物體A作為參考系，則勢能僅取決於另一物體B的相對位置。這時，在不引起混淆的情況下，我們常把“A、B具有的勢能”稱作是“B的勢能”。比如，在電場中的電荷具有靜電勢能，或者是在一個天體附近的另一個天體具有引力勢能。除此之外，有時候保守體系中只存在一個物體，勢能來自於物體內部各部分間的相對位移，這時候我們也說，勢能是這個物體所具有的。比如，彈簧，或者是具有體分布電荷的絕緣體球。
需要注意的是，即使在同一保守力場中的同一處，不同物體的勢能一般也不同，比如在重力作用範圍內，物體的重力勢能不僅取決於其高度，而且還取決於其質量。
