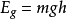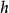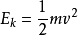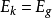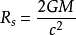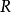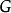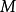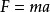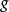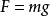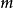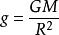史瓦西半徑是任何具有質量的物質都存在的一個臨界半徑特徵值。在物理學和天文學中，尤其在萬有引力理論、廣義相對論中它是一個非常重要的概念。1916年卡爾·史瓦西首次發現了史瓦西半徑的存在，他發現這個半徑是一個球狀對稱、不自轉的物體的重力場的精確解。 一個物體的史瓦西半徑與其質量成正比。太陽的史瓦西半徑約為3千米，地球的史瓦西半徑只有約9毫米。
基本介紹
- 中文名：史瓦西半徑
- 外文名：Schwarzschild radius
- 發現者：卡爾·史瓦西
- 發現時間：1916年
黑洞,半徑公式,分類說明,由來,
黑洞
物體的實際半徑小於其史瓦西半徑的物體被稱為黑洞。在不自轉的黑洞上，史瓦西半徑所形成的球面組成一個視界（僅對於不自轉的黑洞，自轉的黑洞的情況稍許不同）。光和粒子均無法逃離這個球面。銀河中心的超大質量黑洞的史瓦西半徑約為780萬千米。史瓦西半徑不是黑洞實體半徑。黑洞的半徑不能直接用肉眼看，肉眼看到的是史瓦西半徑。
半徑公式
史瓦西半徑（Schwarzschild radius）的公式，其實是從物體逃逸速度的公式衍生而來。該值的含義是，如果特定質量的物質被壓縮到該半徑值之內，將沒有任何已知類型的力可以阻止該物質在自身引力的條件下將自己壓縮成一個黑洞。
根據天體逃逸速度（
）的計算公式計算天體的史瓦西半徑。
推導過程：
將（3）式代入
得
在天體表面，
=
重力勢能
設物體動能為
，要使物體逃脫天體的引力飛向星際空間，則要有
，取該值的臨界值， 
，也就是物體恰好不能逃脫天體引力而飛到星際空間的瞬間值。
即
即
將（4）式變形，得
化簡得
，當
時求R之臨界值（即光恰好不能逃脫天體引力而飛到星際空間瞬間時的天體半徑）。
如果逃逸速度v≤光速
時，物體便再也無法從天體的引力中逃逸到星際空間，會運行在該天體軌道上或者落到天體上。
化簡得
如果逃逸速度v≤光速
此時，即便是光，也無法從這個天體的引力中逃逸到星際空間，這時，這個天體便成了黑洞。
綜上所述，得天體的史瓦西半徑的公式為：
，
為天體的史瓦西半徑，
為萬有引力常數，
為天體的質量，
為光速。
但這並非嚴格推導過程，結論的正確僅僅是一種巧合。
天體的史瓦西半徑即為逃逸速度等於光速時候所得出的
的值。
文字版：天體的史瓦西半徑等於萬有引力常數乘以天體質量乘以二再除以光速的平方。
分類說明
假如一個天體的密度為1000千克/立方厘米，而其質量約為1.5億個太陽質量的話，它的史瓦西半徑會超過它的自然半徑，這樣的黑洞被稱為是超大質量黑洞。絕大多數今天觀察到的黑洞的跡象來自於這樣的黑洞。一般認為它們不是由星群收縮碰撞造成的，而是從一個恆星黑洞開始不斷增長、與其它黑洞合併而形成的。一個星系越大其中心的超大質量黑洞也越大。
恆星黑洞
假如一個天體的密度為核密度（約1.5*10^12千克/立方厘米，相當於中子星的密度）而其總質量在太陽質量的三倍左右則該天體會被壓縮到小於其史瓦西半徑，形成一個恆星黑洞。
微黑洞
小質量的史瓦西半徑也非常小。一個質量相當於喜馬拉雅山的天體的史瓦西半徑只有一納米。目前沒有任何可以想像得出來的原理可以產生這么高的密度。一些理論假設宇宙產生時會產生這樣的小型黑洞。
由來
史瓦西半徑是卡爾·史瓦西（Karl Schwarzschild、也有翻譯做卡爾·史瓦茲旭爾得）於1915年針對廣義相對論方程關於球狀物質分布的解，此解的一個結果是可能存在黑洞。他發現這個半徑是一個球狀對稱、不自轉的物體的重力場的精確解。
根據愛因斯坦的廣義相對論，黑洞是可以預測的。他們發生於史瓦西度量。這是由卡爾·史瓦西於1915年發現的愛因斯坦方程的最簡單解。
