軌跡命題的基本性質
符合某個條件的點的軌跡是圖形F,也就是說:
用以上兩個命題的等價命題表述為:
(1)和(1')保證了沒有一個符合條件的點不在圖形F上,亦即符合條件的點一個也沒有遺漏掉,這叫做軌跡的完備性,另一方面,由於它說明了任意一個點只要合乎某條件就能充分保證它在這個圖形上,因而也叫做充分性。
(2)和(2')保證了圖形F上的點沒有摻雜一個不符合條件的點,這叫做軌跡的
純粹性。另一方面,由於它說明了點要在圖形上,就非合乎某條件不可,因而也叫做
必要性。
兩方面合起來,保證了軌跡上的點不漏不雜。完備性和純粹性是軌跡的基本屬性。軌跡命題的證明必需完成以下兩步: (1 )證完備性;( 2)證純粹性。
軌跡命題的證明
為了確認軌跡命題的真實性,證明軌跡命題“合乎某條件的點的軌跡是圖形F”,要包括兩方面的證明:
1.完備性。任取符合某條件的一點P,證明P在圖形F上。
2.純粹性。在圖形F上任取一點P′,證明P′符合某條件。
也可證明1和2的等價命題:
1′.不在圖形F上的點Q不符合條件。
2′.不符合條件的點Q′不在圖形F上。
綜上所述,證明完備性時,可證1或1′,證明純粹性時,可證2或2′,因此,對一個軌跡命題的證明有四種證法:證1和2,證1和2′,證1′和2,證1′和2′,究竟選用哪種證法要根據實際情況,以便於思考和證明簡捷為選用標準.真實性得到證明的軌跡命題,稱為軌跡定理。
因為初學者對逆否命題不大熟悉,所以—·般多套用第一種,即證明1,2成立,如果第一種不好考慮,再考慮第二、三種,最後考慮第四種。
在初等平面幾何中,通常考慮的軌跡是:線段,直線,圓、圓弧等;在立體幾何中則要考慮平面,球面,旋轉曲面等;在解析幾何中,點的軌跡表現為點的坐標滿足一個或幾個方程或不等式,而滿足方程或不等式這個事實恰恰是集合的點所具有的特殊性質。它將主要研究
圓錐曲線及
超越曲線。
軌跡命題的三種類型
軌跡命題一般按其結論分為三種類型:
①如果給出了軌跡的條件,在結論中又指出了軌跡的形狀、位置和大小(如果有大小的話),如“和兩條平行的定直線等距離的點的軌跡是平行於定直線,且距兩定直線等遠的一條直線”這類軌跡命題叫做第一種類型軌跡命題;
②如果給出了軌跡的條件,在結論中又指出了軌跡的形狀,但沒有指明軌跡的位置和大小(如果有大小的話),如“和兩條平行的定直線等距離的點的軌跡是一條直線”這類軌跡命題叫做第二種類型軌跡命題;
③如果只給出了軌跡的條件,沒有指出軌跡的形狀、位置和大小(如果有大小的話),如“求和兩條平行的定直線等距離的點的軌跡”這類軌跡命題叫做第三種類型軌跡命題。
第一種類型軌跡命題,有條件,又有完全的結論,故可稱為軌跡定理.第二種類型軌跡命題,有條件,有不完全的結論,也可稱為軌跡定理.第三種類型軌跡命題,只有條件,沒有結論,屬於問題的形式,因此稱為軌跡問題。
基本軌跡命題
基本軌跡命題1和一個已知點的距離等於已知長的點的軌跡,是以已知點為圓心,已知長為半徑的圓.如圖1,⊙O是和定點O的距離等於定長r的點的軌跡。
基本軌跡命題2和兩個已知點距離相等的點的軌跡,是連結這兩點的線段的垂直平分線。如圖2,直線l是和已知點A,B距離相等的點的軌跡。
基本軌跡命題3在一個已知角內和角的兩邊距離相等的點的軌跡,是這個角的平分線。如圖3,射線OC是∠AOB內和兩邊OA,OB距離相等的點的軌跡。
推論和兩條相交的已知直線距離相等的點的軌跡,是這兩條直線所成兩組對頂角的平分線。如圖4,l1,l2是和兩相交直線AB,CD距離相等的點的軌跡。
基本軌跡命題4和兩條平行線距離相等的點的軌跡,是和這兩條平行線距離相等的一條平行線。如圖5,直線l是和兩平行線AB,CD距離相等的點的軌跡。
基本軌跡命題5和已知直線的距離等於定長的點的軌跡,是平行於這條直線並且和這條直線的距離等於定長的兩條直線。如圖6,直線l1,l2是和直線AB距離等於定長k的點的軌跡。
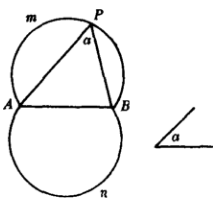
基本軌跡命題6和已知線段的兩個端點的連線的夾角等於已知角的點的軌跡,是以已知線段為弦,所含圓周角等於已知角的兩段弧(端點除外)。如圖7,弧和是和線段AB的兩個端點的連線的夾角等於已知角a的點的軌跡。