合成軌跡(compound locus)是軌跡的一種類型，若軌跡是由兩個或兩個以上的圖形組成，則稱為合成軌跡，若軌跡由一個圖形構成，則稱為單一軌跡。例如，“與相交兩定直線等距的點的軌跡，是兩條互相垂直的直線，它們平分兩定直線的各交角”就是合成軌跡。“和兩定點距離相等的點的軌跡是連結兩定點線段的垂直平分線”是單一軌跡。
基本介紹
- 中文名：合成軌跡
- 外文名：compound locus
- 所屬學科：數學
- 所屬問題：平面幾何(幾何變換與軌跡)
- 相關概念：軌跡問題，軌跡命題
基本介紹,軌跡問題,合成軌跡和單一軌跡,基本軌跡命題,舉例分析,
基本介紹
軌跡問題
有一類軌跡命題只給了條件，而不指明合於此條件的點的軌跡是一個什麼樣的圖形，更不指明軌跡圖形的位置及大小。這類軌跡命題叫求軌跡問題，其表述形式是：“求合於某某條件的點的軌跡’’。
有的求軌跡問題看條件便可斷定軌跡圖形怎樣、位置如何和圖形的大小，但是更多的求軌跡問題則是要經過一番有步驟，有方法的辨識才能獲知軌跡圖形。解這類軌跡命題必須分為兩步。首先辨識清楚軌跡圖形；然後進行兩面證明，很明顯，如果不把軌跡圖形辨識游楚，那么根本就無法進行證明。
合成軌跡和單一軌跡
為此，必須在思想上明確軌跡圖形的概況，以免在辨識中漫無邊際——甚至超出初等幾何範疇。
初等幾何學的平面部分所涉及的幾何圖形不外乎直線類，圓類和直線與圓的結合類(弓形扇形)。因此，平面幾何所涉及的軌跡不外乎如下情況：
單一軌跡：(1)直線類——直線，射線，線段；(2)圓類——圓，弧。
合成軌跡：由兩個或多個單一軌跡合成的軌跡。
所謂合成軌跡，是指由兩個或兩個以上的單一軌跡(點、線、弧形)所合成的軌跡。在求合成軌跡時，要根據題意把平面劃分成幾個區域，在這幾個區域中分別求出符合題意的單一軌跡，然後再合併為所求的合成軌跡。
合成軌跡和單一軌跡是軌跡的一種劃分，由兩個或兩個以上圖形合成的軌跡，叫做合成軌跡；否則叫做單一軌跡。如基本軌跡命題1，2，3，4都是單一命題，基本軌跡命題5，6及基本軌跡命題2的推論都是合成軌跡(參見下文“基本軌跡命題”)。合成軌跡和單一軌跡不是絕對的，往往要看對什麼圖形來說，如某軌跡是一個矩形，若對矩形來說，便是單一軌跡；若對線節(線段包括兩端點)來說，便是合成軌跡。
基本軌跡命題
基本軌跡命題1和一個已知點的距離等於已知長的點的軌跡，是以已知點為圓心，已知長為半徑的圓，如圖1，⊙O是和定點O的距離等於定長r的點的軌跡。
基本軌跡命題2和兩個已知點距離相等的點的軌跡，是連結這兩點的線段的垂直平分線。如圖2，直線l是和已知點A，B距離相等的點的軌跡。
基本軌跡命題3在一個已知角內和角的兩邊距離相等的點的軌跡，是這個角的平分線.如圖3，射線OC是∠AOB內和兩邊OA，OB距離相等的點的軌跡。
推論和兩條相交的已知直線距離相等的點的軌跡，是這兩條直線所成兩組對頂角的平分線。如圖4，l1，l2是和兩相交直線AB，CD距離相等的點的軌跡。
基本軌跡命題4和兩條平行線距離相等的點的軌跡，是和這兩條平行線距離相等的一條平行線，如圖5，直線l是和兩平行線AB，CD距離相等的點的軌跡。
基本軌跡命題5和已知直線的距離等於定長的點的軌跡，是平行於這條直線並且和這條直線的距離等於定長的兩條直線，如圖6，直線l1，l2是和直線AB距離等於定長k的點的軌跡。
基本軌跡命題6和已知線段的兩個端點的連線的夾角等於已知角的點的軌跡，是以已知線段為弦，所含圓周角等於已知角的兩段弧(端點除外).，如圖7，弧和是和線段AB的兩個端點的連線的夾角等於已知角a的點的軌跡。
圖7舉例分析
【例1】以給定圓的心A為頂點任作等腰三角形ABC，自B和C各作該圓的切線，求諸切線交點的軌跡。
自B和C各作切線BM和BN，CK和CL，兩兩相交於E,F, I,J。
1° 交點E和F的軌跡，容易知道它是底邊BC的垂直平分線EAF。
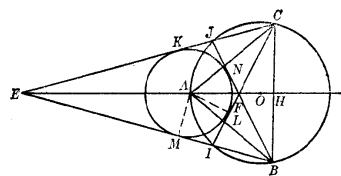圖82° 交點I和J的軌跡，即為三角形ABC的外接圓，因為連AM，AL，則AMB與ALC是兩個全等的直角三角形，於是
∠ABM=∠ACL
因比 ∠CAB=∠CIB
即I在△ABC的外接圓周上。同理，J也在△ABC的外接圓周上，所以I,J的軌跡是ABC三角形的外接圓周。
為此，所求的軌跡就是EAF直線和BAC圓周。
【例2】求到線段AB上點的最短距離為定值d的動點P的軌跡。
圖9解 如圖，過A、B作AB的垂線分別為
。
(1)若動點P在之間(含)的區域，作PQ⊥AB於Q，則
PQ= P到AB的最短距離=d，
所以，動點P的軌跡是在之間(含)的區域中兩條與AB距離為d的平行線段。
(2)若動點P在
的左側區域，則PA= P到AB的最短距離= d，
所以，動點P的軌跡是以A為圓心，d為半徑，位於左側的半圓。
(3)同理，動點P在
右側的軌跡是以B為圓心，d為半徑的半圓。
綜上所述，動點P的軌跡是由(1)、(2)、(3)給出的兩條平行線段及兩個半圓所組成。
