基本軌跡(elementary locus)是一類常用的軌跡。求各種軌跡時，經常把它歸結為求一些簡單的已知軌跡，它們就稱為基本軌跡。通常使用的基本軌跡有以下六種：1.到定點的距離等於定長的點的軌跡是以定點為圓心，定長為半徑的圓；2.和已知線段兩個端點的距離相等的點的軌跡是這條線段的垂直平分線；3.與兩條相交直線距離相等的點的軌跡是平分這兩條直線交角的兩條互相垂直的直線；4.到一條已知直線距離等於定長的點的軌跡，是在已知直線兩旁平行於這條直線，並且到這條直線的距離等於定長的兩條直線；5.與兩條平行直線的距離相等的點的軌跡是這兩條平行線的公垂線段的垂直平分線；6.和已知線段兩個端點連線的夾角等於已知角的點的軌跡，是以已知線段為弦，所含圓周角等於已知角的兩段弧(端點除外)。特別地，當和已知線段兩端點連線的夾角等於直角時，軌跡便是以已知線段為直徑的圓，即兩個半圓周合為一個圓周(兩個端點除外)。
基本介紹
- 中文名：基本軌跡
- 外文名：elementary locus
- 所屬學科：數學
- 所屬問題：平面幾何(幾何變換與軌跡)
- 相關概念：中垂線，角平分線等
基本介紹,基本軌跡1,基本軌跡2,基本軌跡3,基本軌跡4,基本軌跡5,基本軌跡6,基本軌跡7,例題解析,
基本介紹
根據初等幾何中已經有的知識，可得下列七個常用的基本軌跡。
設A、B是兩個定點(圖1)，我們知道，距離A、B兩點等遠的點P，全在AB的中垂線l上；而且AB的中垂線l上的任何一點，距A、B兩點都等遠，即l上沒有距A、B不等遠的點，因此，l是全體距離A、B兩點等遠的點組成的圖形，一個也不多，一個也不少。這是一個基本軌跡。
圖1基本軌跡1
距離兩個已知點等遠的點的軌跡，是這兩點間所連線段的中垂線。
圖2再討論和一個角的兩邊等距的點的軌跡(圖2)，已知和一個角的兩邊等距的點，都在這個角的平分線上，而且角平分線上任一點，都同兩邊等距，據此， 可得基本軌跡2。
基本軌跡2
同已知角兩邊等距的點的軌跡，是這個角的平分線。
注意：說具有某種條件的點的軌跡是某種圖形，要從兩方面考慮。第一，具有這種條件的點必須都在這個圖形上，一個也不能少；第二，這個圖形上的點必須都具有這個條件，也就是說，不能多出來不具有這個條件的點。
基本軌跡3
同兩條平行的已知直線等距的點，是一條直線，它和這兩條已知直線平行，且同它們等距。
如圖3，直線l是同直線l1、l2等距的點的軌跡。自己考慮一下，是否和l1、l2等距的點都在l上?有沒有不在l上的點也和l1、l2等距的?另一方面，還要考慮，l上的點有沒有距離l1、l2不等的?
圖3
圖4再想一個問題，到一條直線l的距離等於定長a的點的軌跡是什麼圖形?容易想到，是和l距離為a的平行線。但要注意，在l兩側都有一條(圖4)，這是基本軌跡4。
基本軌跡4
到一條已知直線距離為定長的點的軌跡，是和已知直線平行的一雙直線，其中每一條到已知直線的距離都等於定長。
基本軌跡5
到一個定點的距離等於定長的點的軌跡，是以定點為圓心，定長為半徑的一個圓(圖5)。
圖5從一點P引出的兩條射線，通過一條線段AB的兩個端點時，這兩條射線所成的角，叫做P點對於線段AB的視角。
基本軌跡6
對於一定線段的視角等於定角的點的軌跡，是以定線段為弦的一雙弓形弧(圖6)。
圖6在軌跡6中，定角是直角時，兩個弓形弧都是半圓，它們合成一個整圓，這是:
基本軌跡7
對於一定線段的視角等於直角的點的軌跡，是以定線段為直徑的一個圓(圖7)。
圖7初等幾何中只研究軌跡是直線或圓的情形、以上七個基本軌跡，是分析其他軌跡問題的基礎。
例題解析
【例1】 求過圓內一點的弦的中點的軌跡。
解:軌跡就是按照一定條件運動的點經過的路線，求軌跡時，先要按照條件畫出動點，畫畫看。
圖8如圖8, P是⊙O內一個定點，過P點作弦，繞P點旋轉，看這動弦中點經過什麼路線，可以看出，如圖中虛線，可能是個圓。
究竟是不是圓呢?如果是，圓心在哪裡，半徑多大?這要具體分析。
設AB是任意一條過P點的弦，看AB的中點M有什麼性質，
∵AM= MB， ∴OM⊥AB，
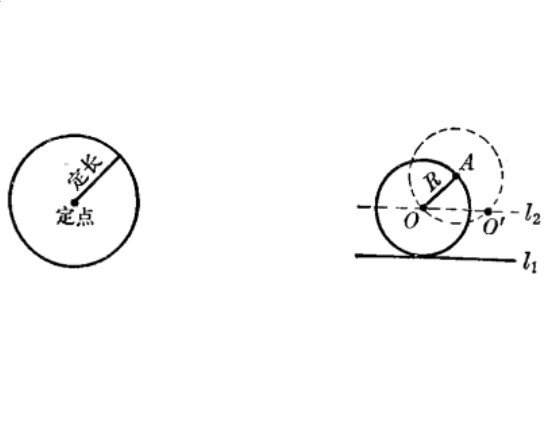
即∠OMP是直角。這就是說，過P點的任意一條弦的中點M，對於線段OP的視角等於直角。因此，全體過P點的弦的中點，都在以OP為直徑的圓周上。
作出以OP為直徑的圓⊙O1(圖中虛線)，所求軌跡是不是這個圓周呢?還要看⊙O1上有沒有不合條件的點。
在⊙O1上任取一點N，連ON，作PN⊥ON，交⊙O於C、D，那么N是CD弦的中點，這說明⊙O1上任何一點都是一條過P點的弦的中點，沒有不符合條件的點。
結果得，過圓內一定點的弦的中點的軌跡，是以圓心和這定點的連線為直徑的一個圓。
有個特殊情況：如果定點P就是圓心O，過P點的弦都是直徑，它們的中點都是O點，這時，軌跡只是O點一個點。
