基本介紹
- 中文名：質量－彈簧－阻尼器系統
- 外文名：Mass-spring-damper system
- 描述：機械振動系統
- 套用：汽車緩衝器
- 學科：機械
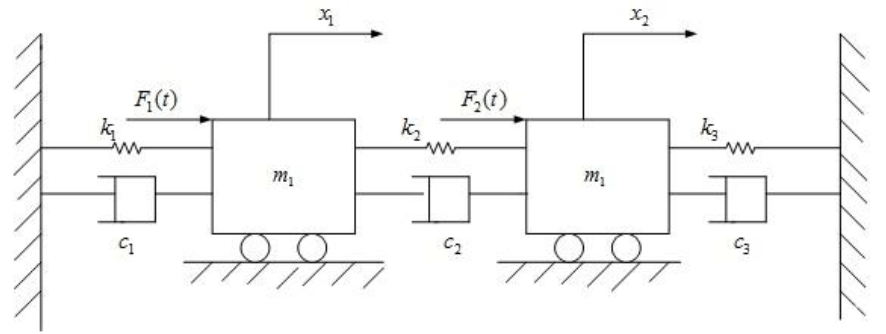
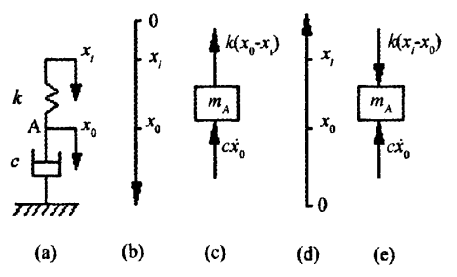
概念,數學模型的建立,研究背景,數軸建模法,研究結論,高層鋼結構調頻液體阻尼器抗震控制最佳化設計,研究背景,TLD簡化模型,研究結論,
概念
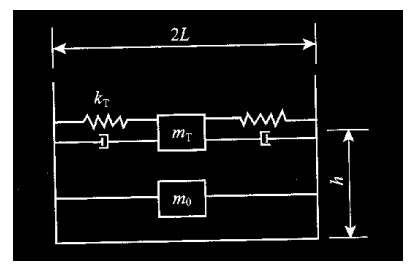
質量－彈簧－阻尼器系統是一種比較普遍的機械振動系統，研究這種系統對於我們的生活和科技也是具有意義的，生活中隨處可見這種系統，例如汽車緩衝器就是一種可以耗減運動能量的裝置，是保證駕駛員行車安全的必備裝置。再者在建築抗震加固措施中引入阻尼器，改變結構的自振特性，增加結構阻尼，吸收地震能量，降低地震作用對建築物的影響。因此研究質量－彈簧－阻尼器系統很具有現實意義。
數學模型的建立
研究背景
數學模型是定量地描述系統的動態特性，揭示系統的結構、參數與動態特性之間關係的數學表達式。其中，微分方程是基本的數學模型，不論是機械的、液壓的、電氣的或熱力學的系統等都可以用微分方程來描述。微分方程的解就是系統在輸入條件下的輸出回響。所以，建立數學模型是研究系統、預測其動態回響的前提。通常情況下，機械振動系統的微分方程都是套用力學中的牛頓定律、質量守恆定律等。
質量－彈簧－阻尼器系統圖
分析這種系統時，首先要根據彈簧、阻尼器的物理意義對與其固連的質量塊進行受力分析，然後用牛頓第
二定律列寫質量塊對應的合力方程，從而得到系統的數學模型——微分方程。在對質量塊進行受力分析時一般遵循這樣的原則：
（1）彈簧受到外作用時，線上性範圍內，彈簧力的大小與彈簧的形變成正比，彈簧力的方向總是與形變方向相反；
（2）尼器可以看作是一個活塞液壓缸系統，當活塞和液壓缸之間存在相對運動時，主動一方總要受到另一方的阻尼力。對於線性阻尼器，阻尼力的大小與阻尼器端點的相對移動速度成正比。外力作用下，當彈簧或阻尼器的兩端點都產生位移時，在確定彈簧形變方向和阻尼器端點相對移動速度時，情況相對有點複雜。針對這一問題，研究提出了一種利用數軸建立彈簧一質量一阻尼系統的數學模型——微分方程的簡單方法，稱之為數軸建模法。
數軸建模法
彈簧、阻尼器、質量塊是組成振動系統的理想元件。在對實際機械結構進行振動分析時，有時可以略去阻尼，系統簡化為質量一彈簧系統。當物理系統的質量很小時，系統就可近似成阻尼一彈簧環節。圖1(a)所示即為阻尼～彈簧環節，已知彈簧的剛度為k，阻尼器的阻尼係數為c，輸入為位移，系統在輸入位移作用下的輸出設為以。來看一下如何用數軸法分析系統受力情況，進而列寫系統的微分方程。
圖1 彈黃一阻尼環節
假設系統的A點處存在一個質量塊mA，這樣可以通過分析其受力情況求得系統的微分方程。由於彈簧和阻尼器都是垂直放置的，故建立一豎直數軸。先來看數軸的正方向朝下的情況。將彈簧和阻尼器端點的位移順序地標在數軸上對應位置，如圖1(b)所示。彈簧在一端受到輸入位移，作用後，另一端點也有位移，屬於兩端都產生位移的情況；阻尼器一端固定，另一個端點有位移輸出。
如果按照一般的物理方法來列寫系統微分方程，也需要取質量塊mA為脫離體，對其進行受力分析。經過能量
損耗後，輸出位移必定小於輸入位移，故彈簧受壓，所受彈簧力向下；質量塊受到彈簧壓力使得阻尼器的活塞桿向下移動，這樣活塞桿將受到缸體施加的向上的阻尼力，此阻尼力傳到質量塊，故mA的受力分析簡圖如圖1(e)所示。可見按照數軸法和一般物理方法求得的系統微分方程是一致的。
從上例可以看出，用數軸法分析系統受力，列寫彈簧一質量一阻尼系統微分方程時，我們無需考慮彈簧的壓縮或拉伸情況，也不用分析阻尼器內部活塞和液壓缸的相互運動情況，只需建立一個數軸，規定原點、正方向和單位長度，把彈簧或阻尼器的輸入位移變數和輸出位移變數當作有理數按照實際順序標在數軸上對應位置。
而彈簧力或阻尼力的方向的確定遵循以下原則：當系統中彈簧兩端或阻尼器兩端都有位移時，彈簧力或阻尼力的方向與所建立的數軸正方向相反；當彈簧或阻尼器只有一端有位移時，彈簧力或阻尼力的方向與彈簧或阻尼器端點的實際位移方向相反。
當彈簧一質量一阻尼系統含有兩個或兩個以上的質量塊時，建立系統數學模型時需對每個質量塊進行受力分析。由於相鄰質量塊間存在負載效應，用數軸法對系統進行受力分析時需考慮第一個進行受力分析的質量塊如何選取。一般來說，前一個質量塊的受力分析總是從相鄰的後一個質量塊受力分析開始。也就是說，第刀個質量塊的受力分析要先考慮第n+1個質量塊對其的作用。因此，可採取這樣一個方法，即：沿著輸入量(力或位移)作用方向尋找最後一個質量塊，按照數軸法先分析其受力情況，然後逆實際運動方向依次分析其餘質量塊的受力情況，進而按照牛頓第二定律列出每個質量塊的受力方程，然後聯立即可得到系統的運動微分方程。
研究結論
數軸建模法是一種簡單有效的建立彈簧一質量一阻尼系統的數學模型的方法。它以數軸知識為基礎，根據系統實際情況建立假想數軸，藉助數軸確定系統中相應質量塊所受彈簧力或阻尼力的大小和方向，進而求得系統微分方程。此方法在建立彈簧一質量一阻尼系統數學模型過程中起到了事半功倍的效果。
高層鋼結構調頻液體阻尼器抗震控制最佳化設計
研究背景
調諧液體阻尼器是一種固定在結構樓層（或頂層）上的水箱。當結構在地震作用下而發生振動時，將帶動水箱一起運動，使水箱中的水晃動起來產生波浪，此波浪對水箱壁的動水壓力就構成了對結構的減振力。國內外對TLD用 於結構風振、地震反應控制研究較多。TLD用於結構抗風抗震控制已處於工程設計和實施階段。面向工程設計，對TLD系統參數取值及簡化設計進行研究，具有一定的套用前景。同時高層鋼結構重量輕、阻尼係數小，所以更易採用結構振動控制技術，研究的主要目的旨在利用單個和多個調頻液體阻尼器減小高層鋼結構地震反應時的參數取值問題及高層鋼結構-調頻液體阻尼器系統抗震控制簡化設計方法，將多個調頻液體阻尼器系統的固有頻率按線性分布進行設計即形成MTLD系統，研究其最優頻頻寬取值及高層鋼結構-MTLD系統簡化設計方法，為調頻液體阻尼器的工程設計和實施提供參考。
TLD簡化模型
採用Housner質量-彈簧模型，引入液體阻尼，從而形成質量-彈簧-阻尼器系統。設某一n層高層鋼結構建築，TLD系統設定於第k層，結構受基底地震加速度擾動輸入，在地震作用下，水箱中的水將產生振動，箱壁產生的動液壓力可分為脈動壓力和振盪壓力，脈動壓力與水箱加速度成正比，但方向相反；振盪壓力取決於液體振盪的波高和頻率。兩種動液壓力可分別採用兩個與箱體聯接形式不同的等效質量的振盪效應來模擬。
TLD簡化模型
研究結論
（1）將單個和多個調頻液體阻尼器引入高層鋼結構抗震中，由於其裝置簡單、經濟，因而具有一定的工程套用前景。
（2）研究根據“高層民用建築鋼結構技術規程”，對高層鋼結構阻尼比取為0.02，對TLDs和MTLD的位置都假定設定於同一樓層。
（3）研究了單個和多個調頻液體阻尼器設計參數，提供的設計參數可供工程設計查用，可以不考慮振型參與係數的影響；設計過程可為設計人員採用。
（4）數值分析及仿真分析表明，採用 目標函式設計的單個和多個調頻液體阻尼器控制效果基本相同。
（5）採用目標函式設計的多個調頻液體阻尼器，較採用目標函式，設計的多個調頻液體阻尼器控制效果好；而且由於MTLD具有一定減震頻頻寬，所以MTLD較TLD/TLDs具有更好的魯棒性。
（6）多振型控制時，可設定多個TLD/TLDs/MTLD系統，忽略振型間的相互作用，仿照本研究的設計思想與方法進行設計。
