愛因斯坦狹義相對論一基本共識。質量能和能量互相轉換這個結論來源於質能公式:E=mc2
基本介紹
- 中文名:質能轉換
- 外文名:mass-energy conversion
- 表達式:E=mc^2
- 提出者:愛因斯坦
- 提出時間:1905
- 套用學科:物理學
基本概念,技術推法,舉例說明,相關理論,
基本概念
他指出,任何具有質量的物體,都貯存著看不見的內能,而且這個由質量貯存起來的能量大到令人難以想像的程度。如果用數學形式表達質量與能量的關係的話,某個物體貯存的能量等於該物體的質量乘以光速的平方。
寫成公式就是:E=mc2。打個比方說,常規狀態下燃燒一噸煤所釋放的全部熱能,只相當於全部由質量轉化而來的0.028毫克物質釋放的能量,但愛因斯坦本人並不認為個常規狀態下一個物質能全部轉化為能量。
而後反物質的發現,使人們了解到,只有當物質與反物質結合時,才會完全泯滅,並轉化為純能量。並推測宇宙誕生之初,正是由能量創造了物質和反物質,而由於一些微妙的不平衡性,我們現在得以生活在物質構成的世界中。然而有人認為這違反了能量守恆,認為能量不可能消失,但科學家的解釋是:“能量沒有消失,而是以物質的形式存在,質量減少得越多,放出的能量也越大。”
技術推法
第一步:要討論能量隨質量變化,先要從量綱得知思路:能量量綱[E]=[M][L]2[T]-2,即能量量綱等於質量量綱和長度量綱的平方以及時間量綱的負二次方三者乘積。我們需要把能量對於質量的函式形式化簡到最簡,那么就要求能量函式中除了質量,最好只有一個其它的變數。把[L]2[T]-2化簡,可以得到只有一個量綱-速度[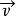 ]的形式:[
]的形式:[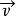 ]×[
]×[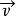 ]。也就是[E]=[M][
]。也就是[E]=[M][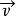 ]×[
]×[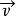 ] 可見我們要討論質能關係,最簡單的途徑是從速度[
] 可見我們要討論質能關係,最簡單的途徑是從速度[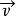 ]下手。
]下手。
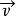
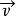
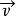
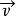
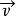
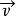
第二步:先要考慮能量的變化 與能量的變化有關的有各種能量形式的轉化,其中直接和質量有關的只有做功。那么先來考慮做工對於能量變化的影響。當外力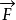 作用在靜止質量為m0質點上時,每產生d
作用在靜止質量為m0質點上時,每產生d (位移
(位移 的微分)的位移,物體能量增加 dE=
的微分)的位移,物體能量增加 dE=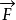 ·d
·d 。考慮最簡化的外力與位移方向相同的情況,上式變成 dE=Fds
。考慮最簡化的外力與位移方向相同的情況,上式變成 dE=Fds
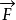


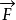

第四步:上式中顯然還要參考m質量這個變數,而我們不想讓質量的加入把我們力和速度的關係複雜化。我們想找到一種辦法約掉m,這樣就能得到純粹的速度和力的關係。參考dE=Fds和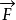 dt=d
dt=d ,我們知道
,我們知道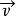 =d
=d /dt 那么可以得到 dE=
/dt 那么可以得到 dE= ·dP_ 如果考慮最簡單的形式:當速度改變和動量改變方向相同:dE=vdP
·dP_ 如果考慮最簡單的形式:當速度改變和動量改變方向相同:dE=vdP
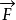

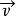


第五步:把上式化成能量和質量以及速度三者的關係式(因為我們最初就是要討論這個形式):dE=vd(mv)----因為dP=d(mv)
第六步:把上式按照微分乘法分解 dE=v2dm+mvdv 這個式子說明:能量的增量含有質量因速度增加而增加dm產生的能量增量和單純速度增加產生的能量增量2個部分。(這個觀點非常重要,在相對論之前,人們雖然在理論物理推導中認識到質量增加也會產生能量增量,但是都習慣性認為質量不會隨運動速度增加而變化,也就是誤以為dm恆定為0,這是經典物理學的最大錯誤之一。)
第七步:我們不知道質量隨速度增加產生的增量dm是怎樣的,現在要研究它到底如何隨速度增加(也就是質量增量dm和速度增量dv之間的直接關係):根據洛侖茲變換推導出的靜止質量和運動質量公式: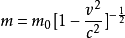 化簡成整數次冪形式:m2=m02[1-(v2/c2)] 化成沒有分母而且m和m0分別處於等號兩側的形式(這樣就是得到運動質量m對於速度變化和靜止質量的純粹的函式形式):m2(c2-v2)=m02c2 用上式對速度v求導得到dm/dv(之所以要這樣做,就是要找到質量增量dm和速度增量dv之間最直接的關係,我們這一步的根本目的就是這個):d[m2(c2-v2)]/dv=d[(m02)c2]/dv(注意式子等號右邊是常數的求導,結果為0) 即 [d(m2)/dv](c2-v2)+m2[d(c2-v2)/dv]=0 即 [m(dm/dv)+m(dm/dv)](c2-v2)+m2(0-2v)=0 即 2m(dm/dv)(c2-v2)-2vm2=0 約掉公因式2m(肯定不是0,呵呵,運動質量為0?沒聽說過) 得到:(dm/dv)(c2-V2)-mv=0 即 (dm/dv)(c2-V2)=mv 由於dv不等於0(我們研究的就是非靜止的情況,運動系速度對於靜止系的增量當然不為0) (c2-v2)dm=mvdv 這就是我們最終得到的dm和dv的直接關係。
化簡成整數次冪形式:m2=m02[1-(v2/c2)] 化成沒有分母而且m和m0分別處於等號兩側的形式(這樣就是得到運動質量m對於速度變化和靜止質量的純粹的函式形式):m2(c2-v2)=m02c2 用上式對速度v求導得到dm/dv(之所以要這樣做,就是要找到質量增量dm和速度增量dv之間最直接的關係,我們這一步的根本目的就是這個):d[m2(c2-v2)]/dv=d[(m02)c2]/dv(注意式子等號右邊是常數的求導,結果為0) 即 [d(m2)/dv](c2-v2)+m2[d(c2-v2)/dv]=0 即 [m(dm/dv)+m(dm/dv)](c2-v2)+m2(0-2v)=0 即 2m(dm/dv)(c2-v2)-2vm2=0 約掉公因式2m(肯定不是0,呵呵,運動質量為0?沒聽說過) 得到:(dm/dv)(c2-V2)-mv=0 即 (dm/dv)(c2-V2)=mv 由於dv不等於0(我們研究的就是非靜止的情況,運動系速度對於靜止系的增量當然不為0) (c2-v2)dm=mvdv 這就是我們最終得到的dm和dv的直接關係。
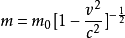
第八步:有了dm的函式,代回到我們第六步的能量增量式 dE=v2dm+mvdv =v2dm+(c2-v2)dm =c2dm 這就是質能關係式的微分形式,它說明:質量的增量與能量的增量成正比,而且比例係數是常數c2。
最後一步:推論出物體從靜止到運動速度為v的過程中,總的能量增量:對上一步的結論進行積分,積分區間取質量從靜止質量m0到運動質量m,得到 ∫dE=∫[m0~m]c2dm 即 E=mc2-m0c2 這就是 物體從靜止到運動速度為v的過程中,總的能量增量。其中 E0=m0c2稱為物體靜止時候的靜止能量。Ev=mc2稱為物體運動時候的總動能(運動總能量)。對於任何已知運動質量為m的物體,可以用E=mc2直接計算出它的運動動能。
舉例說明
是否違背了質量守恆定律
質能方程並不違反質量守恆定律,質量守恆定律是指在任何與周圍隔絕的體系中,不論發生何種變化或過程,其總質量始終保持不變。或者說,化學變化只能改變物質的組成,但不能創造物質,也不能消滅物質,所以該定律又稱物質不滅定律,而質能方程是表述了質量和能量之間關係,所以不違背質量守恆定律。
舉個例子:某人把一粒沙子以光速百分之99.7的速度扔向一堵牆壁,牆會發出巨響並出現裂縫;以光速百分之99.9扔的話那面牆將不復存在。上面這個例子不太準確,當一粒沙子以接近光速飛行時,首先此情況要發生在真空中,否則沙子早由於與空氣的摩擦熔化掉了。其次,由於沙子速度非常高,它會直接穿過牆壁。根據動量守恆定律及質量守恆定律,設沙子質量為m1,以光速c飛行,撞擊牆壁後帶走的那部分質量為m2,其後整體速度為V,則有m1c=(m1+m2)V,穿過牆產生的熱量為Q=0.5m1c2-0.5(m1+m2)V2
相關理論
愛因斯坦的形象比喻
假設有辦法把一個質量僅為1克的小砝碼全部轉化成能量的話,則它的總能量就會相當於2500萬度的電能。愛因斯坦曾作過形象生動的比喻:“只要沒有向外放出的能量,能量就觀察不到。這好比一個非常有錢的人,如果他從來不花費也不供給別人一分錢,那么就沒有誰能說出他有多少財產。”

