簡介 平面幾何中的費馬問題是十七世紀法國數學家、被譽為業餘數學家之王的皮埃爾·德·費馬(Pierre de Fermat,1601–1665)提出的一個著名的幾何問題。
1643年,在一封寫給義大利數學家和物理學家托里拆利(Evangelista Torricelli,1608–1647)的私人信件中,費馬提出了下面這個極富挑戰性和趣味性的幾何難題,請求托里拆利幫忙解答(也有一種說法是費馬本人實際上已經找到了這個問題的答案,他是為了挑戰托里拆利才寫信向他“請教”的):
給定不在一條直線上的三個點 A,B,C,求平面上到這三個點的距離之和最短的點的位置。
圖1.費馬問題 托里拆利成功地解決了費馬的問題。他給出的答案是:
對 △ABC 三條邊的張角都等於120°,即滿足∠APB =∠BPC =∠CPA = 120°的點 P(如下圖所示)就是到點 A,B,C 的距離之和最小的點。
圖2.托里拆利的解答 後來人們就把平面上到一個三角形的三個頂點 A,B,C 距離之和最小的點稱為△ABC的費馬-托里拆利點(Fermat-Torricelli point),也簡稱為費馬點(Fermat point)或托里拆利點(Torricelli point)。
純幾何解法 費馬問題有多種不同的解法,最簡單最快捷最漂亮的還是純幾何解法。
要用幾何方法解決費馬問題,一種思想是把問題中的三條線段 PA, PB, PC“加”在一起或者說拼接在一起,最好是把它們拼接成連線兩個定點的一條折線,這樣一來,因為兩點之間直線最短,就能很快地確定 PA + PB + PC 的最小值。利用
旋轉變換 能成功地把費馬問題中的三條線段以一種非常自然的方式“加到一起”。
圖3.旋轉變換 只要把△BPC繞點B旋轉60°(如上圖所示),設點P轉到了點P',點C轉到了點C',於是就有
PC = P'C', PB = PP' (因為 △PBP' 是等邊三角形)
因此就有
PA + PB + PC = PA + PP' + P'C'
上式的右邊是連線點A和點C'的一段折線的距離,它一定大於或等於線段AC'的長度,所以我們就得到了不等式:
PA + PB + PC = PA + PP' + P'C' ≥ AC'
顯然,如果上面的不等式能取到等號,那么這時候的點P就是到點 A, B, C 距離之和最小的點,也就是費馬點。
探討與證明 若僅用平面幾何和極少量
解析幾何 知識按下列提法討論費馬問題,則由
定義1:在△ABC所在平面上找一點P,使PA+PB+PC的值最小。稱P為其最小點。
定義2:在△ABC中如果有一點P,使∠APB =∠BPC =∠CPA = 120°,則稱P為其費馬點。
定理:如果△ABC的三個內角均小於120°,則其最小點就只能是費馬點;如△ABC有一個內角大於等於120°,則該內角的頂點就是最小點。
證明一 對任意三角形來說最小點不在△ABC外部。
如果最小點在△ABC外部,則可歸納為圖4(1)(含P在一邊延長線上 的情形),圖4(2)兩種情形。
圖4.證明一 在圖4(1)中,顯然,PA+PB+PC>AB+AC;
在圖4(2)中,顯然,PA+PB+PC>P'A+P'B+P'C以上均與P是最小點矛盾,即證。
證明二 銳角三角形的最小點只能是費馬點。
1.最小點不在三條邊上 。 (包括頂點)
假若最小點P在邊上,易知P必是某條邊上高的垂足。不妨設是BC邊上的高AP的垂足。
如圖5(1),以B為圓心,BP為半徑作圖,A,C必在園外,以A,C為焦點作一過P點的橢圓。
P'A+P'C<PA+PC
2.最小點只能是費馬點。
由以上證明知,銳角三角形的最小點P只可能在三角形內部。
如圖5(2)所示:
圖5.證明二 設銳角△ABC的最小點為P,假若AP≥AB,則AP+PB+PB>AB+BC
這與P是最小點矛盾,∴AP<AB
同理,AP<AC(且BP<AB,BP<BC,PC<AC,PC<BC)
以A為圓心,以AP為半徑作圓時,B,C兩點必在該圓外部。
再以B,C為焦點作一橢圓與圓A外切,切點必是P。若切點是另外一點P',則P只能在該橢圓外,這時PB+PC>P'B+P'C也與P為△ABC的最小點矛盾。
過P作圓和橢圓的公切線MN,則∠APM =∠APN=90°。
由橢圓切線性質,知∠MPB =∠NPC
∠APB =∠APM+∠MPB =∠APN+∠NPC =∠APC
同理可證:∠APB =∠BPC
故:∠APB =∠BPC=∠APC=120°
具有 以上特性的點稱為費馬點 。∴P是△ABC的費馬點,又由於銳角三角形的費馬點是存在且唯一,由同一性,銳角三角形的費馬點必是最小點。
證明三 在△ABC中若最大角大於或等於90°而小於120°,則最小點也只能是費馬點。
如圖6,不妨設90°≤ ∠B ≤120°,依據證明二可讓最小點P不在AC上,而若P在AB或BC上,則只能是B點。
圖6.證明三 事實上,若最小點P是BC上而異於B的點,顯然有PA>BA,於是PA+PB+PB>BA+BC,與P為最小點矛盾。然而B也不是最小點。
作出△ABC的費馬點P,延長PB到B',適當選取B’點可使△AB’C的三內角都是銳角,則P也是△AB’C的費馬點,由證明二知P是△AB’C的最小點。
PA+PB'+PC<BA+BB'+BC
不等式兩邊同減BB'
得 PA+PB+PC<BA+BC
B不是△ABC的最小點。
故最小點必在△ABC內部。再依照證明二的證明知,當90°≤ ∠B ≤120°時,最小點也只能是費馬點P。
證明四 在△ABC中若有一個內角大於或等於120°,則該角的頂點就是這個三角形的最小點。
如圖7,由證明三知,最小點不在AC邊上。若最小點在AB或CB邊上,則必是B點。
圖7.證明四 若最小點是△ABC內部的某點P,則仿照證明二的證明知∠APC=120°
但∠APC>∠ABC>120°,矛盾。
最小點必不在△ABC內部,故B點是最小點。
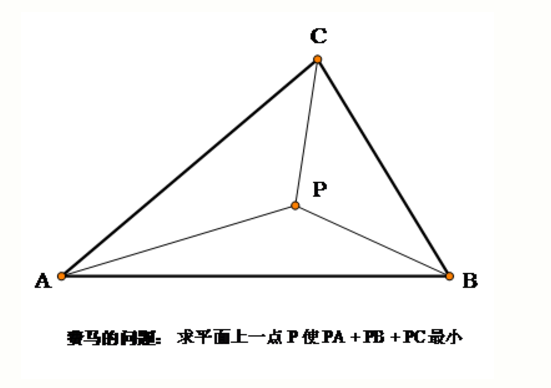 圖1.費馬問題
圖1.費馬問題 圖2.托里拆利的解答
圖2.托里拆利的解答 圖3.旋轉變換
圖3.旋轉變換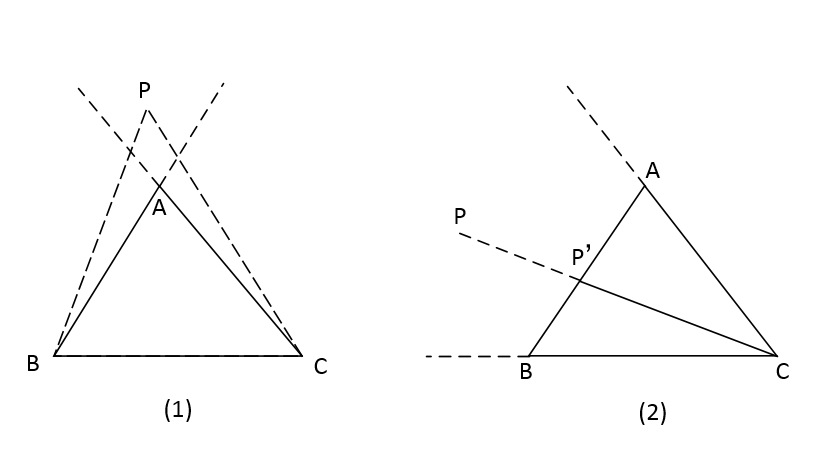 圖4.證明一
圖4.證明一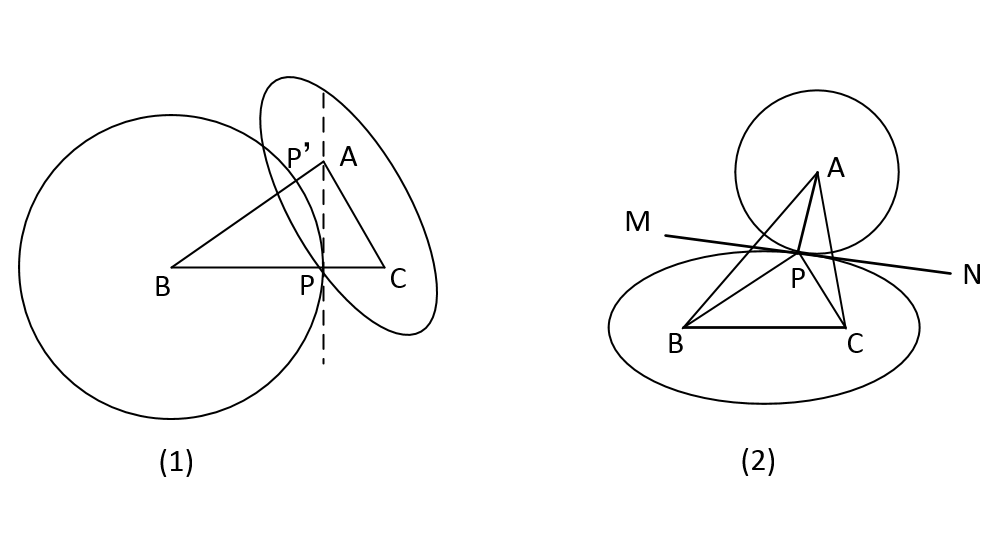 圖5.證明二
圖5.證明二 圖6.證明三
圖6.證明三 圖7.證明四
圖7.證明四
