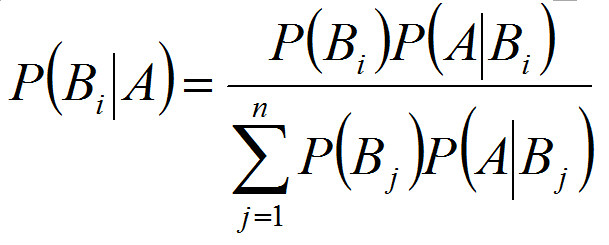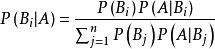基本介紹
- 中文名：貝葉斯定理
- 外文名：Bayes' theorem
- 別稱：托馬斯·貝葉斯定理
- 表達式：P(A|B)=P(A)P(B|A)/P(B)
- 提出者：英國學者貝葉斯
- 提出時間：18世紀
- 套用學科：數學
- 適用領域範圍：機率論
研究意義,定理定義,套用例子,吸毒者檢測,投資決策,其他套用,貝葉斯,
研究意義
人們根據不確定性信息作出推理和決策需要對各種結論的機率作出估計，這類推理稱為機率推理。機率推理既是機率學和邏輯學的研究對象，也是心理學的研究對象，但研究的角度是不同的。機率學和邏輯學研究的是客觀機率推算的公式或規則；而心理學研究人們主觀機率估計的認知加工過程規律。貝葉斯推理的問題是條件機率推理問題，這一領域的探討對揭示人們對機率信息的認知加工過程與規律、指導人們進行有效的學習和判斷決策都具有十分重要的理論意義和實踐意義。
定理定義
貝葉斯公式（發表於1763年）為：
這就是著名的“貝葉斯定理”，一些文獻中把P(B[1])、P(B[2])稱為基礎機率，P(A│B[1])為擊中率，P(A│B[2])為誤報率[1]。
套用例子
吸毒者檢測
貝葉斯定理在檢測吸毒者時很有用。假設一個常規的檢測結果的敏感度與可靠度均為99%，也就是說，當被檢者吸毒時，每次檢測呈陽性（+）的機率為99%。而被檢者不吸毒時，每次檢測呈陰性（-）的機率為99%。從檢測結果的機率來看，檢測結果是比較準確的，但是貝葉斯定理卻可以揭示一個潛在的問題。假設某公司將對其全體雇員進行一次鴉片吸食情況的檢測，已知0.5%的雇員吸毒。我們想知道，每位醫學檢測呈陽性的雇員吸毒的機率有多高？令“D”為雇員吸毒事件，“N”為雇員不吸毒事件，“+”為檢測呈陽性事件。可得
- P(D)代表雇員吸毒的機率，不考慮其他情況，該值為0.005。因為公司的預先統計表明該公司的雇員中有0.5%的人吸食毒品，所以這個值就是D的先驗機率。
- P(N)代表雇員不吸毒的機率，顯然，該值為0.995，也就是1-P(D)。
- P(+|D)代表吸毒者陽性檢出率，這是一個條件機率，由於陽性檢測準確性是99%，因此該值為0.99。
- P(+|N)代表不吸毒者陽性檢出率，也就是出錯檢測的機率，該值為0.01，因為對於不吸毒者，其檢測為陰性的機率為99%，因此，其被誤檢測成陽性的機率為1-99%。
- P(+)代表不考慮其他因素的影響的陽性檢出率。該值為0.0149或者1.49%。我們可以通過全機率公式計算得到：此機率 = 吸毒者陽性檢出率(0.5% x 99% = 0.00495)+ 不吸毒者陽性檢出率(99.5% x 1% = 0.00995)。P(+）=0.0149是檢測呈陽性的先驗機率。用數學公式描述為：
- 根據上述描述，我們可以計算某人檢測呈陽性時確實吸毒的條件機率P(D|+)：
P(D|+) = P(+|D)P(D)/(P(+|D)P(D)+P(+|N)P(N))=0.99 *0.005/0.0149=0.332215
儘管我們的檢測結果可靠性很高，但是只能得出如下結論：如果某人檢測呈陽性，那么此人是吸毒的機率只有大 約33%，也就是說此人不吸毒的可能性比較大。我們測試的條件（本例中指D，雇員吸毒）越難發生，發生誤判的可能性越大。
但如果讓此人再次復檢（相當於P(D)=33.2215%，為吸毒者機率，替換了原先的0.5%），再使用貝葉斯定理計算，將會得到此人吸毒的機率為98.01%。但這還不是貝葉斯定理最強的地方，如果讓此人再次復檢，再重複使用貝葉斯定理計算，會得到此人吸毒的機率為99.98%（99.9794951%）已經超過了檢測的可靠度。
投資決策
貝葉斯定理用於投資決策分析是在已知相關項目B的資料，而缺乏論證項目A的直接資料時，通過對B項目的有關狀態及發生機率分析推導A項目的狀態及發生機率。如果我們用數學語言描繪，即當已知事件Bi的機率P（Bi）和事件Bi已發生條件下事件A的機率P（A│Bi），則可運用貝葉斯定理計算出在事件A發生條件下事件Bi的機率P（Bi│A）。按貝葉斯定理進行投資決策的基本步驟是：
1 列出在已知項目B條件下項目A的發生機率，即將P（A│B）轉換為 P（B│A）；
2 繪製樹型圖；
3 求各狀態結點的期望收益值，並將結果填入樹型圖；
4 根據對樹型圖的分析，進行投資項目決策。
其他套用
搜尋巨人Google和Autonomy，一家出售信息恢復工具的公司，都使用了貝葉斯定理（Bayesian principles）為數據搜尋提供近似的（但是技術上不確切）結果。研究人員還使用貝葉斯模型來判斷症狀和疾病之間的相互關係，創建個人機器人，開發能夠根據數據和經驗來決定行動的人工智慧設備。
貝葉斯
貝葉斯(1701年—1761年) Thomas Bayes，英國數學家。1701年出生於倫敦，做過神父。1742年成為英國皇家學會會員。1761年4月7日逝世。貝葉斯在數學方面主要研究機率論。他首先將歸納推理法用於機率論基礎理論，並創立了貝葉斯統計理論，對於統計決策函式、統計推斷、統計的估算等做出了貢獻。1763年由Richard Price整理髮表了貝葉斯的成果《An Essay towards solving a Problem in the Doctrine of Chances》，對於現代機率論和數理統計都有很重要的作用。貝葉斯的另一著作《機會的學說概論》發表於1758年。貝葉斯所採用的許多術語被沿用至今。
