評價函式

在啟發式搜尋中，用於評價節點重要性的函式叫做評價函式。評價函式的主要任務就是估計等搜尋結點的重要程度，以確定結點的優先權程度。評價函式的一般形式為f(x)=g(x)+h(x); 其中h(x)被稱為啟發函式，構造和選擇合適的啟發函式h(x)是啟發式搜尋的關鍵。

基本介紹

• 中文名：評價函式
• 外文名：Evaluation function
• 所屬領域：人工智慧
• 基本形式：f(x)=g(x)+h(x）
• 所屬學科：計算機
• 套用領域：啟發式搜尋

介紹

在啟發式搜尋過程中，關鍵的一步是如何確定要擴展的節點，不同的確定方法就形成不同的搜尋策略。如果在確定節點時能充分利用與問題求解有關的特性信息，估計出節點的重要性，就能夠在搜尋時選擇重要性較高的節點進行擴展，從而求得最優解。而啟發式搜尋正是這種利用問題自身的某些特性信息，指導搜尋朝著最有希望有方向前進的一種方法。

在啟發式搜尋中，用於評價節點重要性的函式叫做評價函式。評價函式的主要任務就是估計等搜尋結點的重要程度，以確定結點的優先權程度。評價函式的一般形式為

其中 為初始節點 到節點x已經實際付出的代價。當希望有較高的搜尋效率，且只關心到達目標節點的路徑時，g(x)可以忽略，但此時會影響到搜尋的完備性。h(x)為節點x到目標節點Sg的最優路徑的估計代價，它體現了總是的啟發性信息，又稱為啟發函式，其形式要根據總是的特性而定。啟發函式h(x)所攜帶的啟發性的信息越多，搜尋時擴展的節點數就越少，搜尋的效率就越高。因此在確定f(x)時，要使得g(x)與h(x)各占適當的比例。

在實際問題求解時，g(x)可以根據已經搜尋的節點信息計算出來，而啟發函式h(x)依賴於人們的經驗。它來源於我們對問題的某些特性的認識。

基本要求

構造和選擇合適的啟發函式h(x)是啟發式搜尋的關鍵。

在構造h(x) 時，應滿足兩個方面的要求：

1）啟發函式簡單易算；

2）函式要有較高的精確度，能夠反應問題的實際情況。

在實際問題中，這兩個方面的要求是相互制約的，很難同時得到滿足。若將啟發函式設計得簡單易算，那么此函式的精度往往不會很高，產生的誤差也大；若將啟發函式設計得有較高的精確度，那么函式會很複雜，計算也需較長時間。所以構造一個好的啟發函式，要綜合考慮這兩個方面的因素。

基本構造方法

在啟發式圖搜尋策略中，結點n的評價函式f(n)通常表示成：f(n)=g(n)十h(n)，其中g(n)是對從初始結點到結點n的一條最佳路徑上的耗散值g*(n)的估計；h(n)是對從結點n到目標結點的一條最佳路徑上的耗散值h*(n)的估計。值得指出的是,g(n)通常是比較容易計算的。要找到一條最佳路徑，充分條件是啟發式圖搜尋策略必須使每個結點n的h(n)取h*(n)的下界，即h(n)<=h*(n)。當h(n)=0時，啟發式圖搜尋策略運化為廣度優先算法；當h*(n)=h(n)時，啟發式圖搜尋策略所擴展的每一個結點均在最佳路徑上，因而此種情況最好;當某些結點n滿足h(n)>h*(n)時，啟發式圖搜尋策略未必能找到一條最佳路徑。可是在許多實際問題中，尋找一個逼近h*(n)且小於或等於h*(n)的h(n)函式非常困難。一般地,找到一個比較合適的求解路徑就令人滿足了。因此放寬h(n)應滿足的充分條件就成為必要。為了避免因放寬條件而導致圖搜尋策略擴展過多的結點,從而造成接近於寬度優先搜尋那樣的低效率,應使h(n)值與h*(n)值儘可能接近。

逼近法

考慮要求解的問題領域空間：

1).可能的狀態集S1:

2).規則集R1：它能將空間中的一個狀態轉換成領域空間中的另一個狀態

定義問題空間有向圖G=<V,E>。在圖G中，一個結點表示領域空間中的一個狀態，則v表示狀態集s所對應的結點集，若一狀態s經過一條規則變換成另一狀態t，則s和t對應的結點之間有一條從s指向t的有向邊，該邊的權就是套用該規則的費用即規則套用耗散值。而E是所有這樣的有向邊的集合。於是，要求解的問題可表述成：在圖G中尋找一條從初始結點(初態)到目標結點(目標狀態)的比較合適的路徑。

再考慮相似問題領域空間：

1).可能的狀態集S2:

2).規則集R2：該規則集與要求解的問題領域空間中的規則集R,在某種程度上有其相似性,且能將原領域空間的一個狀態轉換成相似問題空間中的另一個狀態。

因此,所謂相似問題僅僅是指求解原問題所用規則的不同,且原問題求解所用的規則集與相似問題求解所用的規則在某種程度上(如規則使用條件的相以性,規則使用效果的相似性)相似。相似問題求解所用的規則一般通過減弱(或加強)原問題求解所用的規則的使用條件而得到。

函式逼近法

啟發式圖搜尋策略的本質就是依據啟發信息來選擇結點擴展，因此可以依據諸啟發信息來建立h(n)函式。

設 ，其中， 是結點n的第i個啟發信息值， 是與其對應項有關的權。對線性函式來說，可以使用最小二乘法確定權重。

注意

函式逼近法是基於數學表達式逼近h*(n)，而相似問題逼近法則基於將一個問題轉化為另一個問題，且用高效率的算法求解轉化後的問題所得到角最佳路徑上的耗散值來通近h*(n)。由於h(n)的計算工作量是影響啟發能力的一個至關重要的因素,因此,在用相似問題逼近法時,所設計的求解相似問題的算法一定要高效率且運行時間很短,在用函式逼近法時，h(n)函式的數學表達式一定要易於計算。

影響

可採納性

一個啟發式算法是否能被採納，要看採用該算法能否達到預期的目標。比如說在圖搜尋中，如果存在從初始節點到目標節點解答路徑的情況下，一個算法能夠找到最小代價的解答路徑，則稱該算法具有可採納性。否則就可能找不到目標節點，或者找到的不是代價最小的解答路徑，從而該算法可能失去其可採納性。如在八數碼遊戲中，廣度優先搜尋算法，儘管其搜尋空間非常大，效率非常低，但總能找到最小的解答路徑，所以該算法是可採納的。

希望函式強弱

我們用h(n)接近h*(n)的程度來衡量希望函式強弱.當h(n)< h*(n)且差距大時，稱希望函式過弱，易於產生較大的搜尋空間。比如當h(n)= 0時,希望函式最弱，從而產生了最大的搜尋空間(廣度優先搜尋)。但是,當h(n)≥ h*(n)時，希望函式過強，又可能使算法失去可採納性。

從右圖可以看出，當希望函式對評價函式值的影響過強時，搜尋將向縱深方向進行。當希望函式對評價函式值的影響過弱時，搜尋將向廣度水平方向進行。

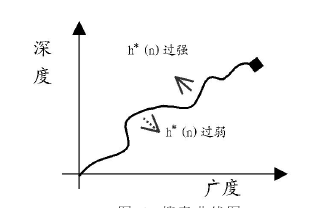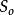
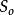
評價函式對希望函式的影響