蘭道定理

蘭道定理又稱競賽圖定理，是一個定義在有向圖上的概念，顧名思義，它可以想像成n個人兩兩對決，贏得向輸的連邊，其實就是給一副完全圖的無向邊定了方向。

基本介紹

• 中文名：蘭道定理
• 外文名：Landau's Theorem
• 學科：數學
• 又名：競賽圖定理

前言

競賽圖(tournament)是一個定義在有向圖上的概念，顧名思義，它可以想像成nn個人兩兩對決，贏得向輸的連邊，其實就是給一副完全圖的無向邊定了方向。
競賽圖有很多十分優美的性質，比如說在之前的最長路徑我就介紹了其關於曼哈頓路徑的一些性質。
在這裡，我們要介紹一個判定競賽圖的優美定理——蘭道定理(Landau’s Theorem)，這個定理在1953年被Landau, H.G.證明。目前，這個定理在國內競賽圈還不算普及，雖然在部分oj上有少數用到這個定理的題目（如：HDU5873），但是在國區域網路站上還沒有找到任何證明。

定義

定義一個競賽圖的比分序列(score sequence)，是把競賽圖的每一個點的出度從小到大排列得到的序列。

一個長度為n的序列，是合法的比分序列若且唯若：

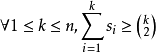
證明

首先這個定理的必要性是顯然的：即任一n階競賽圖都滿足這個條件。
現在我們只需要證明這個定理的充分性。
在這裡，我們的證明是一個構造算法。思路是從一個一般競賽圖開始，每次改變兩條邊的方向，構造出一個比分序列是給定序列的競賽圖。
假設有一個一個滿足定理條件的序列s。現在我們構造一個及其平凡的n階競賽圖Tn，這個競賽圖的第ii個節點向所有j<i的j節點都連有向邊，因此其比分序列是(0,1,...,n−1)，我們要從這個平凡競賽圖開始構造。
考慮當前構造到了一個競賽圖U，它的比分序列u滿足

當k=n時顯然要取等號。

顯然初始時Tn滿足這個條件的。
令α為第一個滿足sα>uα的位置，這個位置顯然存在不然就代表我們構造成功了。令β表示最後一個滿足uα=uβ的位置。
再考慮γγ是第一個滿足sγ<uγ的位置，這個位置肯定要嚴格大於β，而且這個位置為什麼一定存在呢？因為但是β及其以前的位置s都是要大於等於u的。
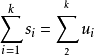
我們畫一下這些位置大概是這樣排列的：

蘭道序列