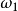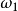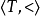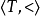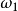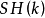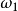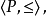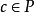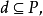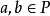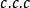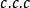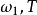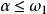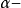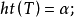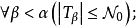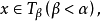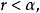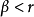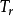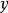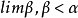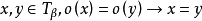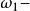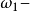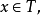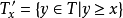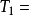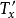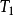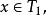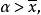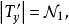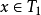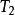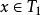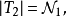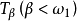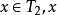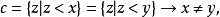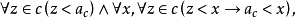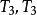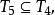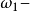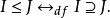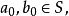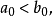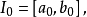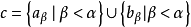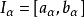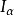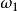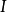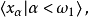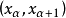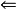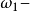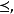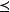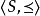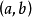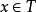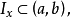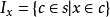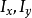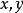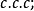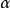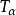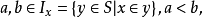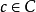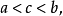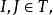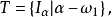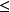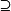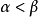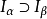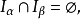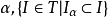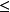蘇斯林樹

蘇斯林樹是一種無窮樹，指高度為ω₁，每條鏈及反鏈均可數的樹。研究蘇斯林樹的直接動機是解決蘇斯林假設，蘇斯林樹概念最先由庫雷巴(Kurepa,D.)於1936年提出，他證明“存在蘇斯林樹”等價於“存在蘇斯林線”，後來，美國數學家米勒(Miller,D.)於1943年證明蘇斯林假設等價於“不存在蘇斯林樹”，美國學者傑希(Jech,T.J.)與延森(Jensen,R.)等人證明了“蘇斯林樹存在”相容且獨立於ZFC公理系統，蘇斯林樹的概念可以從ω₁推廣到任意基數上。設κ為一個無窮基數，若〈T，<〉為高度為κ且T中每條鏈及反鏈的基數均小於κ，則稱樹〈T，<〉為一棵κ蘇斯林樹，因此ω₁蘇斯林樹即為蘇斯林樹，也有些文獻將“不存在κ蘇斯林樹”稱為廣義蘇斯林假設，記為SH(κ)。

除了對ω₁蘇斯林樹的研究已經獲得許多重要結果外，人們對一般的κ蘇斯林樹的研究也獲得了許多有趣的結果。

基本介紹

• 中文名：蘇斯林樹
• 外文名：Suslin tree
• 所屬學科：數學
• 相關問題：蘇斯林假設
• 提出者：庫雷巴

基本介紹

蘇斯林樹是一種無窮樹，指高度為，每條鏈及反鏈均可數的樹。研究蘇斯林樹的直接動機是解決蘇斯林假設，蘇斯林樹概念最先由庫雷巴(Kurepa,D.)於1936年提出，他證明“存在蘇斯林樹”等價於“存在蘇斯林線”，後來，美國數學家米勒(Miller,D.)於1943年證明蘇斯林假設等價於“不存在蘇斯林樹”，美國學者傑希(Jech,T.J.)與延森(Jensen,R.)等人證明了“蘇斯林樹存在”相容且獨立於ZFC公理系統，蘇斯林樹的概念可以從推廣到任意基數上。設κ為一個無窮基數，若為高度為κ且T中每條鏈及反鏈的基數均小於κ，則稱樹為一棵κ蘇斯林樹，因此蘇斯林樹即為蘇斯林樹，也有些文獻將“不存在κ蘇斯林樹”稱為廣義蘇斯林假設，記為。

除了對蘇斯林樹的研究已經獲得許多重要結果外，人們對一般的κ蘇斯林樹的研究也獲得了許多有趣的結果。

相關結論

設P 為一線性序集 稱P是稠密的，若對P的任意a，b， 當a<b 時，存在 使得a<c<b，稱P 為完全的，若它的每一個非空有界子集有上確界，又設 稱d在P中稠密，若對任意 ，存在e∈d使得a<e<b，稱P是可分的，若P有可數稠密子集，稱P 為滿足可數鏈條件(Countable chain condition，簡稱)，若P的每一個開區間的不交族都是至多可數的，顯然，若P可分，則P滿足 。

實直線R 是無界稠密完全可分的線性序集，並且有理數集Q是它的稠密子集。

蘇斯林(Suslin) 在1920 年提出一個問題，把實直線R 滿足的條件中“可分”減弱為“ ”,這樣的集合存在嗎?我們把無界稠密完全滿足 且不可分的線性序集稱為蘇斯林線(Suslinline)。

定義1 樹T稱為蘇斯林樹(Suslin tree)，若T 的高為 的每一個鏈(枝) 和反鏈都是至多可數的。

定義2令樹T稱為正規的，若

[1]

[2] T有唯一最小元，即

[3]

[4] 若x不是T的極大元，則x 的分叉數是無窮的；

[5] 對任一個所有當時，在上存在使得；

[6] T是唯一極限的，即當時，。

引理若存在蘇斯林樹，則存在 正規蘇斯林樹。

證明：設T是蘇斯林樹，我們分五步來構造所要求的正規蘇斯林樹。方法是把T 的一些點刪除掉或添加一些點而得到正規蘇斯林樹。1*設若是至多可數的，則把x刪去，而得{|是不可數的}。具有性質：若而則在上存在y使得可見T₁滿足[5],2*設而x無分叉，則刪去x而得={|x上有分叉}，則否則T₁上有分叉的點在某個層之下，於是T₁必有不可數長度的枝，這與題設矛盾，這時，T₂滿足[1]、[3]、[5] 和[4*]。

[4* ]：對每一個至少有兩個分叉。

3* 若c是T₂中的鏈，且有性質則把a_c添加到T₂上使得由此得滿足[1]、[3]、[4*]、[5] 和[6]。4* 令T₄是T₃ 中處於極限層的點所組成，則T₄滿足[1][3][4][5]。5* 令使[2]成立，則T₅是正規蘇斯林樹.

定理存在蘇斯林線的充要條件為存在蘇斯林樹。證()設S是蘇斯林線。我們來構造蘇斯林樹T，T由S的非退化(即端點不重合) 的閉區間所組成，若令

任取使令若的構成，令是的端點組成的集，則c可數，因S是蘇斯林線，它是不可分的。由c的可數性必得c在S中不稠密，於是存在一區間[a，b] 與c 不交，從而我們可選某個有上述性質的區間令所以可定。

令則T不可數，以(即以)關係偏序T，若，則或因為對每一個被良序，故T為樹。

T沒有不可數的無窮反鏈，因為，若不可比較，則它們是S上不交區間，由於S滿足故T的每一個反鏈是至多可數的。

T沒有不可數無窮枝，若b是一長度為的枝，則的的左端點形成S的遞增無窮序列從而開區間形成不可數集。這與S滿足 矛盾。由T的構造可知。

() 設T是正規蘇斯林樹，我們證明T的所有枝組成的蘇斯林線，我們可在T上定義線性序則T的所有元在元下形成序集。我們證明S是蘇斯林線，S是稠密的，若是S上一區間，則我們可找到使得其中。若不交，則在T上不可比較，於是S 的開區間不交族至多可數。S 滿足S不可分。事實上，設C為T的枝組成的任一可數集，令是大於C中每一個枝長度的可數序數，x是上任一點，設則不存在使得可見C不是S的稠密子集。